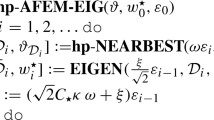Skip to main content
Springer Nature Link
Log in

Convergence and optimality of \({\mathbf {hp}}\)-AFEM

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

We design and analyze an adaptive hp-finite element method (\({\mathbf {hp}}\)-AFEM) in dimensions \(n=1,2\). The algorithm consists of iterating two routines: \({\mathbf {hp}}\)-NEARBEST finds a near-best hp-approximation of the current discrete solution and data to a desired accuracy, and REDUCE improves the discrete solution to a finer but comparable accuracy. The former hinges on a recent algorithm by Binev for adaptive hp-approximation, and acts as a coarsening step. We prove convergence and instance optimality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Ainsworth, M., Senior, B.: An adaptive refinement strategy for \(hp\)-finite element computations. Appl. Numer. Math. 26(1–2), 165–178 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  2. Babuška, I., Craig, A., Mandel, J., Pitkäranta, J.: Efficient preconditioning for the \(p\)-version finite element method in two dimensions. SIAM J. Numer. Anal. 28(3), 624–661 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bank, R., Parsania, A., Sauter, S.: Saturation estimates for hp-finite element methods. Comput. Vis. Sci. 16(5), 195–217 (2013)

    Article  MathSciNet  Google Scholar 

  4. Binev, P.: Instance optimality for hp-type approximation. Oberwolfach Rep. 39, 14–16 (2013)

    Google Scholar 

  5. Binev, P.: Tree approximation for \(hp\)-adaptivity (in preparation)

  6. Binev, P., Dahmen, W., DeVore, R.: Adaptive finite element methods with convergence rates. Numer. Math. 97(2), 219–268 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Binev, P., DeVore, R.: Fast computation in adaptive tree approximation. Numer. Math. 97(2), 193–217 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  8. Braess, D., Pillwein, V., Schöberl, J.: Equilibrated residual error estimates are \(p\)-robust. Comput. Methods Appl. Mech. Eng. 198(13–14), 1189–1197 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Brix, K., Campos Pinto, M., Canuto, C., Dahmen, W.: Multilevel preconditioning of discontinuous Galerkin spectral element methods. Part I: geometrically conforming meshes. IMA J. Numer. Anal. 35(4), 1487–1532 (2015)

  10. Bürg, M., Dörfler, W.: Convergence of an adaptive \(hp\) finite element strategy in higher space-dimensions. Appl. Numer. Math. 61(11), 1132–1146 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Canuto, C., Nochetto, R.H., Verani, M.: Adaptive Fourier–Galerkin methods. Math. Comput. 83, 1645–1687 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Canuto, C., Nochetto, R.H., Verani, M.: Contraction and optimality properties of adaptive Legendre–Galerkin methods: the 1-dimensional case. Comput. Math. Appl. 67(4), 752–770 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  13. Canuto, C., Simoncini, V., Verani, M.: Contraction and optimality properties of an adaptive Legendre–Galerkin method: the multi-dimensional case. J. Sci. Comput. 63(3), 769–798 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  14. Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods. Fundamentals in Single Domains. Scientific Computation. Springer, Berlin (2006)

  15. Canuto, C., Verani, M.: On the numerical analysis of adaptive spectral/\(hp\) methods for elliptic problems. In: Analysis and Numerics of Partial Differential Equations. Springer INdAM Series, vol. 4, pp. 165–192. Springer, Milan (2013)

  16. Cascon, J.M., Kreuzer, Ch., Nochetto, R.H., Siebert, K.G.: Quasi-optimal convergence rate for an adaptive finite element method. SIAM J. Numer. Anal. 46(5), 2524–2550 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Carstensen, C., Feischl, M., Page, M., Praetorius, D.: Axioms of adaptivity. Comput. Math. Appl. 67(6), 1195–1253 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Dahmen, W., Scherer, K.: Best approximation by piecewise polynomials with variable knots and degrees. J. Approx. Theory 26(1), 1–13 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  19. Demkowicz, L., Oden, J.T., Rachowicz, W., Hardy, O.: Toward a universal \(h\)-\(p\) adaptive finite element strategy. I. Constrained approximation and data structure. Comput. Methods Appl. Mech. Eng. 77(1–2), 79–112 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  20. Demkowicz, L., Rachowicz, W., Devloo, Ph.: A fully automatic \(hp\)-adaptivity. J. Sci. Comput. 17(1–4), 127–155 (2002)

  21. DeVore, R., Scherer, K.: Variable knot, variable degree spline approximation to \(x^\beta \). In: Quantitative Approximation (Proceedings of the International Symposium. Bonn, 1979), pp. 121–131. Academic Press, New York (1980)

  22. Dörfler, W.: A convergent adaptive algorithm for Poisson’s equation. SIAM J. Numer. Anal. 33(3), 1106–1124 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Dörfler, W., Heuveline, V.: Convergence of an adaptive \(hp\) finite element strategy in one space dimension. Appl. Numer. Math. 57(10), 1108–1124 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Eibner, T., Melenk, J.M.: An adaptive strategy for \(hp\)-FEM based on testing for analyticity. Comput. Mech. 39(5), 575–595 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ern, A., Vohralík, M.: Polynomial-degree-robust a posteriori estimates in a unified setting for conforming, nonconforming, discontinuous Galerkin, and mixed discretizations. SIAM J. Numer. Anal. 53(2), 1058–1081 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  26. Gui, W., Babuška, I.: The \(h,\;p\) and \(h\)-\(p\) versions of the finite element method in \(1\) dimension. II. The error analysis of the \(h\)- and \(h\)-\(p\) versions. Numer. Math. 49(6), 613–657 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  27. Gui, W., Babuška, I.: The \(h,\;p\) and \(h\)-\(p\) versions of the finite element method in \(1\) dimension. III. The adaptive \(h\)-\(p\) version. Numer. Math. 49(6), 659–683 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  28. Guo, B., Babuška, I.: The \(hp\)-version of the finite element method i: the basic approximation results. Comput. Mech. 1, 21–41 (1986)

    Article  MATH  Google Scholar 

  29. Guo, B., Babuška, I.: The \(hp\)-version of the finite element method ii: general results and applications. Comput. Mech. 1, 203–226 (1986)

    Article  MATH  Google Scholar 

  30. Guo, B., Babuška, I.: Regularity of the solutions for elliptic problems on nonsmooth domains in \( R^3\). II. Regularity in neighbourhoods of edges. Proc. R. Soc. Edinb. Sect. A 127(3), 517–545 (1997)

  31. Houston, P., Senior, B., Süli, E.: \(hp\)-discontinuous Galerkin finite element methods for hyperbolic problems: error analysis and adaptivity. Int. J. Numer. Methods Fluids 40(1–2), 153–169 (2002) [ICFD Conference on Numerical Methods for Fluid Dynamics (Oxford, 2001)]

  32. Houston, P., Süli, E.: A note on the design of \(hp\)-adaptive finite element methods for elliptic partial differential equations. Comput. Methods Appl. Mech. Eng. 194(2–5), 229–243 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  33. Mavriplis, C.: Adaptive mesh strategies for the spectral element method. Comput. Methods. Appl. Mech. Eng. 116, 77–86 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  34. Melenk, J.M., Wohlmuth, B.I.: On residual-based a posteriori error estimation in \(hp\)-FEM. Adv. Comput. Math. 15(1–4), 311–331 (2002)

    MathSciNet  MATH  Google Scholar 

  35. Morin, P., Nochetto, R.H., Siebert, K.G.: Data oscillation and convergence of adaptive FEM. SIAM J. Numer. Anal. 38(2), 466–488 (2000) (electronic)

  36. Nochetto, R.H., Siebert, K.G., Veeser, A.: Theory of adaptive finite element methods: an introduction. In: Multiscale, Nonlinear and Adaptive Approximation, pp. 409–542. Springer, Berlin (2009)

  37. Oden, J.T., Demkowicz, L., Rachowicz, W., Westermann, T.A.: Toward a universal \(h\)-\(p\) adaptive finite element strategy. II. A posteriori error estimation. Comput. Methods Appl. Mech. Eng. 77(1–2), 113–180 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  38. Oden, J.T., Patra, A., Feng, Y.: An \(hp\) Adaptive Strategy, vol. 157, pp. 23–46. ASME Publication, New York (1992)

  39. Rachowicz, W., Oden, J.T., Demkowicz, L.: Toward a universal \(h\)-\(p\) adaptive finite element strategy. III. Design of \(h\)-\(p\) meshes. Comput. Methods Appl. Mech. Eng. 77(1–2), 181–212 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  40. Schwab, Ch.: \(p\)- and \(hp\)-Finite Element Methods. Oxford University Press, Oxford (1998)

    MATH  Google Scholar 

  41. Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54(190), 483–493 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  42. Schmidt, A., Siebert, K.G.: A posteriori estimators for the \(h\)-\(p\) version of the finite element method in 1D. Appl. Numer. Math. 35(1), 43–66 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  43. Schötzau, D., Schwab, C., Wihler, T.: \(hp\)-dgfem for elliptic problems in polyhedra i: stability and quasi-optimality on geometric meshes. SIAM J. Numer. Anal. 51(3), 1610–1633 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  44. Schötzau, D., Schwab, C., Wihler, T.: \(hp\)-dgfem for elliptic problems in polyhedra ii: exponential convergence. SIAM J. Numer. Anal. 51(4), 2005–2035 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  45. Stevenson, R.: Optimality of a standard adaptive finite element method. Found. Comput. Math. 7(2), 245–269 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  46. Veeser, A.: Approximating gradients with continuous piecewise polynomial functions. Found. Comput. Math. (2015). doi:10.1007/s10208-015-9262-z

    MATH  Google Scholar 

Download references

Acknowledgments

C. Canuto and M. Verani are partially supported by GNCS-INdAM and the Italian research Grant Prin 2012 2012HBLYE4 “Metodologie innovative nella modellistica differenziale numerica”. R. H. Nochetto is partially supported by NSF Grants DMS-1109325 and DMS-1411808. We would like to thank the referees for their insightful comments and suggestions.

Author information

Authors and Affiliations

  1. Dipartimento di Scienze Matematiche, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Turin, Italy

    Claudio Canuto

  2. Department of Mathematics and Institute for Physical Science and Technology, University of Maryland, College Park, MD, USA

    Ricardo H. Nochetto

  3. Korteweg-de Vries Institute for Mathematics, University of Amsterdam, P.O. Box 94248, 1090 GE, Amsterdam, The Netherlands

    Rob Stevenson

  4. MOX, Dipartimento di Matematica, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133, Milan, Italy

    Marco Verani

Authors
  1. Claudio Canuto
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ricardo H. Nochetto
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rob Stevenson
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Marco Verani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Marco Verani.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Canuto, C., Nochetto, R.H., Stevenson, R. et al. Convergence and optimality of \({\mathbf {hp}}\)-AFEM . Numer. Math. 135, 1073–1119 (2017). https://doi.org/10.1007/s00211-016-0826-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-016-0826-x

Mathematics Subject Classification