Skip to main content
SpringerLink
Log in

On a heuristic stopping rule for the regularization of inverse problems by the augmented Lagrangian method

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

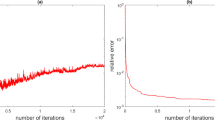
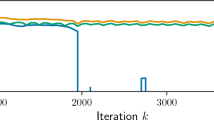
In this paper we propose a heuristic stopping rule of Hanke–Raus type for the regularization of linear ill-posed inverse problems by the augmented Lagrangian method. This stopping rule requires no information on the noise level. Under certain source conditions, we derive a posteriori error estimates in term of Bregman distance. By imposing certain conditions on the noise data, we establish convergence results. Numerical results are presented to illustrate the performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Bakushinskii, A.B.: Remarks on choosing a regularization parameter using the quasioptimality and ratio criterion. USSR Comput. Math. Math. Phys. 24(4), 181–182 (1984)

    Article  Google Scholar 

  2. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3, 1–122 (2011)

    Article  MATH  Google Scholar 

  3. Daubechies, I., Defrise, M., De Mol, C.: An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 57, 1413–1457 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  4. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems, vol. 375. Springer, Berlin (1996)

    Book  MATH  Google Scholar 

  5. Fortin, M., Glowinski, R.: Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems. North-Holland Publ. Co, Amsterdam (1983)

    MATH  Google Scholar 

  6. Frick, K., Grasmair, M.: Regularization of linear ill-posed problems by the augmented Lagrangian method and variational inequalities. Inverse Probl. 28(10), 104005 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Frick, K., Lorenz, D., Resmerita, E.: Morozov’s principle for the augmented Lagrangian method applied to linear inverse problems. Multiscale Model. Simul. 9(4), 1528–1548 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Frick, K., Scherzer, O.: Regularization of ill-posed linear equations by the non-stationary augmented Lagrangian method. J. Integral Equ. Appl. 22(2), 217–257 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  9. Güler, O.: On the convergence of the proximal point algorithm for convex minimization. SIAM J. Control Optim. 29(2), 403–419 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hanke, M., Raus, T.: A general heuristic for choosing the regularization parameter in ill-posed problems. SIAM J. Sci. Comput. 17(4), 956–972 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hansen, P.C., O’Leary, D.P.: The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 14, 1487–1503 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hofmann, B., Kaltenbacher, B., Pöschl, C., Scherzer, O.: A convergence rates result for Tikhonov regularization in Banach spaces with non-smooth operators. Inverse Prob. 23, 987–1010 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Ito, K., Kunisch, K.: Lagrange Multiplier Approach to Variational Problems and Applications. SIAM, Philadelphia (2008)

    Book  MATH  Google Scholar 

  15. Jin, B., Lorenz, D.A.: Heuristic parameter-choice rules for convex variational regularization based on error estimates. SIAM J. Numer. Anal. 48(3), 1208–1229 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Jin, Q.: Hanke–Raus heuristic rule for variational regularization in Banach spaces. Inverse Probl. 32, 085008 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jin, Q., Stals, L.: Nonstationary iterated Tikhonov regularization for ill-posed problems in Banach spaces. Inverse Probl. 28, 104011 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jin, Q., Zhong, M.: Nonstationary iterated Tikhonov regularization in Banach spaces with uniformly convex penalty terms. Numer. Math. 127, 485–513 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Kindermann, S., Neubauer, A.: On the convergence of the quasioptimality criterion for (iterated) Tikhonov regularization. Inverse Probl. Imaging 2(2), 291–299 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Powell, M.J.D.: A method for nonlinear constraints in minimization problems. In: Fletcher, R. (ed.) Optimization, pp. 283–298. Academic Press, New York (1969)

    Google Scholar 

  21. Rockafellar, R.T.: Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Math. Oper. Res. 1(2), 97–116 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  22. Schuster, T., Kaltenbacher, B., Hofmann, B. and Kazimierski, K.S.: Regularization Methods in Banach Spaces, Radon Series on Computational and Applied Mathematics 10. Walter de Gruyter, Berlin (2012)

  23. Tikhonov, A.N., Glasko, V.B., Kriksin, J.A.: On the question of quasi-optimal choice of a regularized approximation. Dokl. Akad. Nauk. 248, 531–535 (1979)

    MathSciNet  MATH  Google Scholar 

  24. Wahba, G.: The approximate solution of linear operator equations when data are noisy. SIAM J. Numer. Anal. 14, 651–667 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zălinscu, C.: Convex Analysis in General Vector Spaces. World Scientific Publishing Co. Inc, River Edge (2002)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematical Sciences Institute, Australian National University, Canberra, ACT, 2601, Australia

    Qinian Jin

Authors
  1. Qinian Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qinian Jin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jin, Q. On a heuristic stopping rule for the regularization of inverse problems by the augmented Lagrangian method. Numer. Math. 136, 973–992 (2017). https://doi.org/10.1007/s00211-016-0860-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-016-0860-8

Mathematics Subject Classification

Search

Navigation