Numerical schemes and rates of convergence for the Hamilton–Jacobi equation continuum limit of nondominated sorting

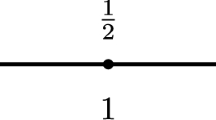
Abstract

Non-dominated sorting arranges a set of points in n-dimensional Euclidean space into layers by repeatedly removing the coordinatewise minimal elements. It was recently shown that nondominated sorting of random points has a Hamilton–Jacobi equation continuum limit. The obvious numerical scheme for this PDE has a slow convergence rate of $O(h^\frac{1}{n})$. In this paper, we introduce two new numerical schemes that have formal rates of O(h) and we prove the usual $O(\sqrt{h})$ theoretical rates. We also present the results of numerical simulations illustrating the difference between the formal and theoretical rates.

A Properties of finite differences

We give the proof of Lemma 7 here.

Proof

We proceed by induction. The base case of $N=2$ is exactly Proposition 1(ii). Assume (4.8) holds for some $N\ge 2$. Then by the inductive hypothesis and base case

$$\begin{aligned} D^\pm _k(u_1\cdots u_N u_{N+1})&= (u_1 \cdots u_N) D^\pm _k u_{N+1} + u_{N+1}D^\pm _k (u_1\dots u_N) \nonumber \\&\quad \pm \, hD^\pm _k (u_1\cdots u_N) D^\pm _k u_{N+1}\nonumber \\&= \sum _{j=1}^{N+1} D^\pm _k u_j\prod _{i\ne j} u_i + u_{N+1}\sum _{j=2}^N (\pm h)^{j-1} \sum _{|I|=j} \prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i\nonumber \\&\quad \pm \, hD^\pm _k (u_1\cdots u_N) D^\pm _k u_{N+1}. \end{aligned}$$

(A.1)

Notice that

$$\begin{aligned}&\pm hD^\pm _k (u_1\cdots u_N) D^\pm _k u_{N+1}\nonumber \\&= \pm h D^\pm _k u_{N+1}\left( \sum _{j=1}^N D^\pm _k u_j\prod _{i\ne j} u_i + \sum _{j=2}^N (\pm h)^{j-1} \sum _{|I|=j} \prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i \right) \nonumber \\&= \sum _{j=1}^N \pm h D^\pm _k u_{N+1}D^\pm _k u_j\prod _{i\ne j} u_i + \sum _{j=2}^N (\pm h)^j \sum _{|I|=j} D^\pm _k u_{N+1}\prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i\nonumber \\&= \sum _{j=2}^{N+1} (\pm h)^{j-1} \sum _{\begin{array}{c} |I|=j \\ N+1 \in I \end{array}} \prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i, \end{aligned}$$

(A.2)

where in the final summation, $I \subset \{1,\dots ,N+1\}$. We also have

$$\begin{aligned} u_{N+1}\sum _{j=2}^N (\pm h)^{j-1} \sum _{|I|=j} \prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i = \sum _{j=2}^{N+1} (\pm h)^{j-1} \sum _{\begin{array}{c} |I|=j \\ N+1 \not \in I \end{array}} \prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i. \end{aligned}$$

Combining this with (A.1) and (A.2) we have

$$\begin{aligned} D^\pm _k(u_1\cdots u_N u_{N+1}) = \sum _{j=1}^{N+1}D^\pm _k u_j \prod _{i\ne j} u_i+ \sum _{j=2}^{N+1} (\pm h)^{j-1} \sum _{|I|=j} \prod _{i \in I} D_k^\pm u_i \prod _{i\not \in I} u_i. \end{aligned}$$

This verifies (4.8) for $N+1$. The proof is completed by mathematical induction. $\square$