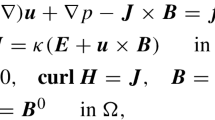Skip to main content
Springer Nature Link
Log in

New analysis of mixed FEMs for dynamical incompressible magnetohydrodynamics

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

This paper focuses on a new error analysis and a recovering technique of frequently-used mixed FEMs for a dynamical incompressible magnetohydrodynamics (MHD) system. The methods use the standard inf-sup stable Taylor–Hood/MINI velocity-pressure space pairs to solve the Navier–Stokes equations and the Nédélec’s edge element for solving the magnetic field. We establish new and optimal error estimates. In particular, we prove that the method provides the optimal accuracy for the MINI element in \(L^2\)-norm and for the Taylor-Hood element in \(H^1\)-norm. The analysis is based on a modified Maxwell projection and the corresponding estimates in negative norms, while all the existing analysis is not optimal due to the strong coupling of system and the pollution of the lower-order Nédélec’s edge approximation in analysis. In addition, at any given time step, we develop a simple recovery technique for numerical approximation to the magnetic field of one order higher accuracy in the spatial direction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Armero, F., Simo, J.C.: Long-term dissipativity of time-stepping algorithms for an abstract evolution equation with applications to the incompressible MHD and Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 131, 41–90 (1996)

    MathSciNet  MATH  Google Scholar 

  2. Badia, S., Codina, R., Planas, R.: On an unconditionally convergent stabilized finite element approximation of resistive magnetohydrodynamics. J. Comput. Phys. 234, 399–416 (2013)

    MathSciNet  MATH  Google Scholar 

  3. Cao, C., Wu, J.: Two regularity criteria for the 3D MHD equations. J. Differ. Equ. 248, 2263–2274 (2010)

    MathSciNet  MATH  Google Scholar 

  4. Chae, D.: Nonexistence of self-similar singularities in the viscous magnetohydrodynamics with zero resistivity. J. Funct. Anal. 254, 441–453 (2008)

    MathSciNet  MATH  Google Scholar 

  5. Chen, Q., Miao, C., Zhang, Z.: On the regularity criterion of weak solution for the 3D viscous magneto-hydrodynamics equations. Commun. Math. Phys. 284, 919–930 (2008)

    MathSciNet  MATH  Google Scholar 

  6. Costabel, M., Dauge, M.: Singularities of electromagnetic fields in polyhedral domains. Arch. Ration. Mech. Anal. 151, 221–276 (2000)

    MathSciNet  MATH  Google Scholar 

  7. Davidson, P.A.: An Introduction to Magnetohydrodynamics. Cambridge University Press, Cambridge (2001)

    MATH  Google Scholar 

  8. Ding, Q., Mao, S.: A convergent finite element method for the compressible magnetohydrodynamics system. J. Sci. Comput. 82(21), 1–29 (2020)

    MathSciNet  MATH  Google Scholar 

  9. Gao, H., Qiu, W.: A semi-implicit energy conserving finite element method for the dynamical incompressible magnetohydrodynamics equations. Comput. Methods Appl. Mech. Eng. 346, 982–1001 (2019)

    MathSciNet  MATH  Google Scholar 

  10. Gao, H., Sun, W.: An efficient fully linearized semi-implicit Galerkin-mixed FEM for the dynamical Ginzburg-Landau equations of superconductivity. J. Comput. Phys. 294, 329–345 (2015)

    MathSciNet  MATH  Google Scholar 

  11. Gao, H., Li, B., Sun, W.: Stability and error estimates of fully discrete Galerkin FEMs for nonlinear thermistor equations in non-convex polygons. Numer. Math. 136, 383–409 (2017)

    MathSciNet  MATH  Google Scholar 

  12. Gerbeau, J.F., Le Bris, C., Leliévre, T.: Mathematical Methods for the Magnetohydrodynamics of Liquid Metals. Numerical Mathematics and Scientific Computation. Oxford University Press, New York (2006)

    MATH  Google Scholar 

  13. He, Y., Zou, J.: A priori estimates and optimal finite element approximation of the MHD flow in smooth domains. ESAIM Math. Model. Numer. Anal. 52, 181–206 (2018)

    MathSciNet  MATH  Google Scholar 

  14. He, Y.: Unconditional convergence of the Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. IMA J. Numer. Anal. 35(2), 767–801 (2015)

    MathSciNet  MATH  Google Scholar 

  15. Hiptmair, R.: Finite elements in computational electromagnetism. Acta. Numer. 11, 237–239 (2002)

    MathSciNet  MATH  Google Scholar 

  16. Hu, K., Ma, Y., Xu, J.: Stable finite element methods preserving \(\nabla \cdot \textbf{B} =0\) exactly for MHD models. Numer. Math. 135, 371–396 (2017)

    MathSciNet  MATH  Google Scholar 

  17. Hu, K., Xu, J.: Structure-preserving finite element methods for stationary MHD models. Math. Comput. 88, 553–581 (2019)

    MathSciNet  MATH  Google Scholar 

  18. Huang, Y., Qiu, W., Sun, W.: New analysis of mixed finite element methods for incompressible Magnetohydrodynamics, submitted, arXiv:abs/4217665 (2021)

  19. Hughes, W.F., Young, F.J.: The Electromagnetics of Fluids. Wiley, New York (1966)

    Google Scholar 

  20. Johanna, R.: Convergence of a finite difference scheme for two-dimensional incompressible magnetohydrodynamics. SIAM J. Numer. Anal. 54, 3550–3576 (2016)

    MathSciNet  MATH  Google Scholar 

  21. Larson, M.G., Bengzon, F.: The Finite Element Method: Theory, Implementation, and Applications. Springer, Belin (2013)

    MATH  Google Scholar 

  22. Li, B., Wang, J., Xu, L.: A convergent linearized Lagrange finite element method for the magneto-hydrodynamic equations in two-dimensional nonsmooth and nonconvex domains. SIAM J. Numer. Anal. 58, 430–459 (2020)

    MathSciNet  MATH  Google Scholar 

  23. Li, B., Sun, W.: Unconditional convergence and optimal error estimates of a Galerkin-mixed FEM for incompressible miscible flow in porous media. SIAM J. Numer. Anal. 51, 1959–1977 (2013)

    MathSciNet  MATH  Google Scholar 

  24. Li, F., Shu, C.W.: Locally divergence-free discontinuous Galerkin methods for MHD equations. J. Sci. Comput. 22, 413–442 (2005)

    MathSciNet  MATH  Google Scholar 

  25. Li, F., Xu, L., Yakovlev, S.: Central discontinuous Galerkin methods for ideal MHD equations with the exactly divergence-free magnetic field. J. Comput. Phys. 230, 4828–4847 (2011)

    MathSciNet  MATH  Google Scholar 

  26. Li, L., Zheng, W.: A robust solver for the finite element approximation of stationary incompressible MHD equations in 3D. J. Comput. Phys. 351, 254–270 (2017)

    MathSciNet  MATH  Google Scholar 

  27. Li, L., Ni, M., Zheng, W.: A charge-conservative finite element method or inductionless MHD equations. Part I: Convergence. SIAM J. Sci. Comput. 41, B796–B815 (2019)

    MathSciNet  MATH  Google Scholar 

  28. Lin, F., Zhang, P.: Global small solutions to an MHD-type system: the three-dimensional case. Commun. Pure Appl. Math. 67, 531–580 (2014)

    MathSciNet  MATH  Google Scholar 

  29. Logg, A., Mardal, K., Wells, G. (eds.): Automated Solution of Differential Equations by the Finite Element Method. Springer, Berlin (2012)

    MATH  Google Scholar 

  30. Moreau, R.: Magneto-hydrodynamics. Kluwer, Dordrecht (1990)

    Google Scholar 

  31. Monk, P.: Finite Element Methods for Maxwell’s Equations. Oxford University Press, New York (2003)

    MATH  Google Scholar 

  32. Pagliantini, C.: Computational Magnetohydrodynamics with Discrete Differential Forms, Ph.D Thesis, ETH, Zürich (2016)

  33. Phillips, E.G., Elman, H.C.: A stochastic approach to uncertainty in the equations of MHD kinematics. J. Comput. Phys. 284, 334–350 (2015)

    MathSciNet  MATH  Google Scholar 

  34. Phillips, E.G., Shadid, J.N., Cyr, E.C., Elman, H.C., Pawlowski, R.P.: Block preconditioners for stable mixed nodal and edge finite element representations of incompressible resistive MHD. SIAM J. Sci. Comput. 38(6), B1009–B1031 (2016)

    MathSciNet  MATH  Google Scholar 

  35. Prohl, A.: Convergent finite element discretizations of the nonstationary incompressible magnetohydrodynamic ssystem, ESAIM: Math. Model. Numer. Anal. 42, 1065–1087 (2008)

    MATH  Google Scholar 

  36. Qiu, W., Shi, K.: A mixed DG method and an HDG method for incompressible magnetohydrodynamics. IMA J. Numer. Anal. 40(2), 1356–1389 (2020)

    MathSciNet  MATH  Google Scholar 

  37. Salah, N.B., Soulaimani, A., Habashi, W.G.: A finite element method for magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 190, 5867–5892 (2001)

    MathSciNet  MATH  Google Scholar 

  38. Schonbek, M.E., Schonbek, T.P., Suli, E.: Large-time behaviour of solutions to the magneto-hydrodynamics equations. Math. Ann. 304(1), 717–756 (1996)

    MathSciNet  MATH  Google Scholar 

  39. Schneebeli, A., Schötzau, D.: Mixed finite elements for incompressible magneto-hydrodynamics. C. R. Acad. Sci. Paris Ser. I 337(1), 71–74 (2003)

    MathSciNet  MATH  Google Scholar 

  40. Sermange, M., Temam, R.: Some mathematics questions related to the MHD equations. Commun. Pure Appl. Math. 36, 635–664 (1983)

    MATH  Google Scholar 

  41. Schötzau, D.: Mixed finite element methods for stationary incompressible magnetohydrodynamics. Numer. Math. 96, 315–341 (2004)

    MathSciNet  MATH  Google Scholar 

  42. Sun, W.: Analysis of lowest-order characteristics-mixed FEM for miscible displacement in porous media. SIAM J. Numer. Anal. 59, 1875–1895 (2021)

    MathSciNet  MATH  Google Scholar 

  43. Sun, W., Wu, C.: New analysis of Galerkin-mixed FEMs for miscible displacement in porous media. Math. Comput. 90, 81–102 (2021)

    MATH  Google Scholar 

  44. Wathen, M., Greif, C.: A scalable approximate inverse block preconditioner for an incompressible magnetohydrodynamics model problem. SIAM J. Sci. Comput. 42(1), B57–B79 (2020)

    MathSciNet  MATH  Google Scholar 

  45. Wathen, M., Greif, C., Schötzau, D.: Preconditioners for mixed finite element discretizations of incompressible MHD equations. SIAM J. Sci. Comput. 39(6), A2993–A3013 (2017)

    MathSciNet  MATH  Google Scholar 

  46. Yang, J., Mao, S., He, X., Yange, X., He, Y.: A diffuse interface model and semi-implicit energy stable finite element method for two-phase magnetohydrodynamic flows. Comput. Methods Appl. Mech. Eng. 356, 435–464 (2019)

    MathSciNet  MATH  Google Scholar 

  47. Zhang, G., He, Y., Yang, D.: Analysis of coupling iterations based on the finite element method for stationary magnetohydrodynamics on a general domain. Comput. Math. Appl. 68(7), 770–788 (2014)

    MathSciNet  MATH  Google Scholar 

  48. Zhang, G., Yang, J., Bi, C.: Second order unconditionally convergent and energy stable linearized scheme for MHD equations. Adv. Comput. Math. 44, 505–540 (2018)

    MathSciNet  MATH  Google Scholar 

  49. Zhang, G., Zhang, Y., He, Y.: Two-level coupled and decoupled parallel correction methods for stationary incompressible magnetohydrodynamics. J. Sci. Comput. 65(3), 920–939 (2015)

    MathSciNet  MATH  Google Scholar 

  50. Zhao, J., Mao, S., Zheng, W.: Anisotropic adaptive finite element method for magnetohydrodynamic flow at high Hartmann numbers. Appl. Math. Mech. (Engl. Ed.) 37(11), 1479–1500 (2016)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author would like to thank the anonymous referees for the careful review and valuable suggestions and comments, which have greatly improved this article.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics and Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, People’s Republic of China

    Huadong Gao

  2. Department of Mathematics, City University of Hong Kong, 83 Tat Chee Avenue, Kowloon, Hong Kong, People’s Republic of China

    Weifeng Qiu

  3. Research Center for Mathematics, Advanced Institute of Natural Science, Beijing Normal University, Zhuhai, People’s Republic of China

    Weiwei Sun

  4. Guangdong Provincial Key Laboratory of Interdisciplinary, Research and Application for Data Science (IRADS), BNU-HKBU United International College, Zhuhai, 519087, People’s Republic of China

    Weiwei Sun

Authors
  1. Huadong Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Weifeng Qiu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Weiwei Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Weifeng Qiu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The work of the author was supported in part by the National Science Foundation of China (11871234 and 12231003) and Hubei Key Laboratory of Engineering Modeling and Scientific Computing. The work of W. Qiu was supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. CityU 11302718). The work of W. Sun was partially supported by the National Natural Science Foundation of China (12231003 and 12071040), Guangdong Provincial Key Laboratory IRADS (2022B1212010006, UIC-R0400001-22) and Guangdong Higher Education Upgrading Plan (UIC-R0400024-21).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, H., Qiu, W. & Sun, W. New analysis of mixed FEMs for dynamical incompressible magnetohydrodynamics. Numer. Math. 153, 327–358 (2023). https://doi.org/10.1007/s00211-022-01341-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-022-01341-9

Mathematics Subject Classification