Accurate computation of the zeros of the generalized Bessel polynomials

Summary.

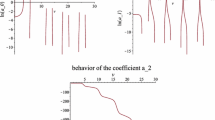
A general method for approximating polynomial solutions of second-order linear homogeneous differential equations with polynomial coefficients is applied to the case of the families of differential equations defining the generalized Bessel polynomials, and an algorithm is derived for simultaneously finding their zeros. Then a comparison with several alternative algorithms is carried out. It shows that the computational problem of approximating the zeros of the generalized Bessel polynomials is not an easy matter at all and that the only algorithm able to give an accurate solution seems to be the one presented in this paper.