Summary.
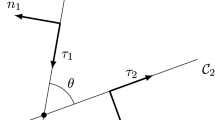
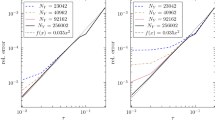
We study here the finite element approximation of the vector Laplace-Beltrami Equation on the sphere \(S^2\). Because of the lack of a smooth parametrization of the whole sphere (the so-called “poles problem”), we construct a finite element basis using two different coordinate systems, thus avoiding the introduction of artificial poles. One of the difficulties when discretizing the Laplace operator on the sphere, is then to recover the optimal order error. This is achieved here by a suitable perturbation of the vector field basis, locally, near the matching region of the coordinate systems.
Similar content being viewed by others
Author information
Authors and Affiliations
Additional information
Received July 16, 1998 / Published online December 6, 1999
Rights and permissions
About this article
Cite this article
Simonnet, E. A variational crime on the tangent bundle of the sphere. Numer. Math. 85, 409–431 (2000). https://doi.org/10.1007/s002110000169
Issue Date:
DOI: https://doi.org/10.1007/s002110000169