Abstract
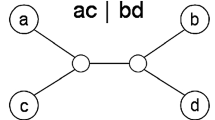
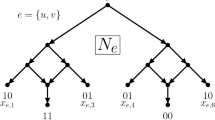
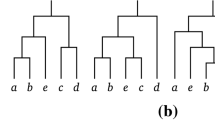
Let S be a set of n taxa. Given a parameter k and a set of quartet topologies Q over S such that there is exactly one topology for every subset of four taxa, the parameterized Minimum Quartet Inconsistency (MQI) problem is to decide whether we can find an evolutionary tree inducing a set of quartet topologies that differs from the given set in at most k quartet topologies. The best fixed-parameter algorithm devised so far for the parameterized MQI problem runs in time O(4k n+n 4). In this paper, first we present an O(3.0446k n+n 4) fixed-parameter algorithm and an O(2.0162k n 3+n 5) fixed-parameter algorithm for the parameterized MQI problem. Finally, we give an O *((1+ε)k) fixed-parameter algorithm, where ε>0 is an arbitrarily small constant.
Similar content being viewed by others
References
Ben-Dor, A., Chor, B., Graur, D., Ophir, R., Pelleg, D.: From four-taxon trees to phylogenies: the case of mammalian evolution. In: Proceedings of the RECOMB, pp. 9–19 (1998)
Bandelt, H.J., Dress, A.: Reconstructing the shape of a tree from observed dissimilarity data. Adv. Appl. Math. 7, 309–343 (1986)
Berry, V., Jiang, T., Kearney, P.E., Li, M., Wareham, H.T.: Quartet cleaning: Improved algorithms and simulations. In: Proceedings of the 7th Annual European Symposium on Algorithms (ESA 99). Lecture Notes in Comput. Sci., vol. 1643, pp. 313–324. Springer, Berlin (1999)
Cho, B.: From quartets to phylogenetic trees. In: Proceedings of the 25th Conference on Current Trends in Theory and Practice of Informatics (SOFSEM). Lecture Notes in Comput. Sci., vol. 1521, pp. 36–53. Springer, Berlin (1998)
Downey, R.G., Fellows, M.R.: Parameterized Complexity. Springer, Berlin (1999)
Erdős, P., Steel, M., Székely, L., Warnow, T.: A few logs suffice to build (almost) all trees (Part 1). Random Struct. Algorithms 14, 153–184 (1999)
Greene, D.H., Knuth, D.E.: Mathematics for the Analysis of Algorithms, 2nd edn. Progress in Computer Science. Birkhäuser, Boston (1982)
Gramm, J., Niedermeier, R.: A fixed-parameter algorithm for minimum quartet inconsistency. J. Comput. Syst. Sci. 67, 723–741 (2003)
Jiang, T., Kearney, P.E., Li, M.: Some open problems in computational molecular biology. J. Algorithms 34, 194–201 (2000)
Jiang, T., Kearney, P.E., Li, M.: A polynomial time approximation scheme for inferring evolutionary tree from quartet topologies and its application. SIAM J. Comput. 30, 1942–1961 (2001)
Steel, M.: The complexity of reconstructing trees from qualitative characters and subtrees. J. Classif. 9, 91–116 (1992)
Niedermeier, R.: Invitation to Fixed-Parameter Algorithms. Oxford University Press, London (2006)
Niedermeier, R., Rossmanith, P.: A general method to speed up fixed-parameter algorithms. Inf. Process. Lett. 73, 125–129 (2000)
Wu, G., You, J.-H., Lin, G.: A lookahead branch-and-bound algorithm for the maximum quartet consistency problem. In: Proceedings of WABI 2005. Lecture Notes in Comput. Sci., vol. 3692, pp. 65–76. Springer, Berlin (2005)
Wu, G., You, J.-H., Lin, G.: A polynomial time algorithm for the minimum quartet inconsistency problem with O(n) quartet errors. Inf. Process. Lett. 100, 167–171 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by NSC-DAAD Sandwich Program and partially supported by the National Science Council of Taiwan under grant no. NSC 96-2221-E-194-045-MY3, and was carried out at RWTH Aachen University, Germany. A preliminary version of this paper appeared in the Proceedings of the 3rd International Workshop on Parameterized and Exact Computation (IWPEC), Lecture Notes in Computer Science, vol. 5018, pp. 66–77.
Rights and permissions
About this article
Cite this article
Chang, MS., Lin, CC. & Rossmanith, P. New Fixed-Parameter Algorithms for the Minimum Quartet Inconsistency Problem. Theory Comput Syst 47, 342–367 (2010). https://doi.org/10.1007/s00224-009-9165-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-009-9165-y