Skip to main content
Springer Nature Link
Log in

Approximately Counting Approximately-Shortest Paths in Directed Acyclic Graphs

  • Published:
Theory of Computing Systems Aims and scope Submit manuscript

Abstract

Given a directed acyclic graph with non-negative edge-weights, two vertices s and t, and a threshold-weight L, we present a fully-polynomial time approximation-scheme for the problem of counting the s-t paths of length at most L. This is best possible, as we also show that the problem is #P-complete. We then show that, unless P=NP, there is no finite approximation to the bi-criteria version of the problem: count the number of s-t paths of length at most L 1 in the first criterion, and of length at most L 2 in the second criterion. On the positive side, we extend the approximation scheme for the relaxed version of the problem, where, given thresholds L 1 and L 2, we relax the requirement of the s-t paths to have length exactly at most L 1, and allow the paths to have length at most L 1′ : = (1+δ)L 1, for any δ > 0.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. Note that due to the lack of cycles, the problems of looking for shortest and longest paths on DAGs are computationally identical.

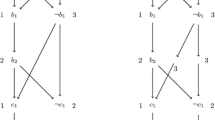
  2. To see this, observe that in a topologically sorted graph G, any subset of V∖{s,t} gives a unique candidate for an s-t path.

References

  1. Broder, A.Z., Mayr, E.W.: Counting minimum weight spanning trees. J. Algorithm. 24, 171–176 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  2. Buhmann, J.M., Mihalák, M., Šrámek, R., Widmayer, P.: Robust optimization in the presence of uncertainty. In: Proceedings of the 4th Conference on Innovations in Theoretical Computer Sciencei (ITCS). pp. 505–514. ACM, New York (2013)

  3. Burge, C., Karlin, S.: Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 268(1), 78–94 (1997)

    Article  Google Scholar 

  4. Chen, T., Kao, M.Y., Tepel, M., Rush, J., Church, G.M.: A dynamic programming approach to de novo peptide sequencing via tandem mass spectrometry. J. Comput. Biol. 8(3), 325–337 (2001)

    Article  Google Scholar 

  5. Durbin, R., Eddy, S.R., Krogh, A., Mitchison, G.: Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press (1998)

  6. Dyer, M., Frieze, A., Kannan, R., Kapoor, A., Perkovic, L., Vazirani, U.: A mildly exponential time algorithm for approximating the number of solutions to a multidimensional knapsack problem. Comb. Probab. Comput. 2(3), 271–284 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  7. Gopalan, P., Klivans, A., Meka, R., Štefankovič, D., Vempala, S., Vigoda, E.: An FPTAS for # knapsack and related counting problems. In: Proceedings of the 52nd Annual IEEE Symposium on Foundations of Computer Science (FOCS). pp. 817–826 (2011)

  8. Jerrum, M.: Two-dimensional monomer-dimer systems are computationally intractable. J. Stat. Phys. 48(1–2), 121–134 (1987)

    Article  MathSciNet  Google Scholar 

  9. Karp, R.M.: Reducibility Among Combinatorial Problems. Springer (1972)

  10. Kreher, D.L., Stinson, D.R.: Combinatorial Algorithms: Generation, Enumeration, and Search (1998)

  11. Lu, B., Chen, T.: A suboptimal algorithm for de novo peptide sequencing via tandem mass spectrometry. J. Comput. Biol. 10(1), 1–12 (2003)

    Article  Google Scholar 

  12. Naor, D., Brutlag, D.: On suboptimal alignments of biological sequences. In: Proceedings of the 4th Annual Symposium on Combinatorial Pattern Matching (CPM). pp. 179–196. Springer (1993)

  13. Rizzi, R., Tomescu, A.I.: Combinatorial decomposition approaches for efficient counting and random generation fptases. CoRR abs/1307.2347v2 (2013)

  14. Štefankovič, D., Vempala, S., Vigoda, E.: A deterministic polynomial-time approximation scheme for counting knapsack solutions. SIAM J. Comput. 41(2), 356–366 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  15. Valiant, L.G.: The complexity of computing the permanent. Theor. Comput. Sci. 8(2), 189–201 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  16. Valiant, L.G.: The complexity of enumeration and reliability problems. SIAM J. Comput. 8(3), 410–421 (1979)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

We thank Octavian Ganea and anonymous reviewers for their suggestions and comments. The work has been partially supported by the Swiss National Science Foundation under grant no. 200021_138117/1, and by the EU FP7/2007-2013, under the grant agreement no. 288094 (project eCOMPASS).

Author information

Authors and Affiliations

  1. Institute of Theoretical Computer Science, Department of Computer Science, ETH Zurich, Switzerland

    Matúš Mihalák, Rastislav Šrámek & Peter Widmayer

Authors
  1. Matúš Mihalák
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Rastislav Šrámek
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Peter Widmayer
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Rastislav Šrámek.

Additional information

Preliminary version of this paper appeared at the 11th Workshop on Approximation and Online Algorithms (WAOA 2013).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mihalák, M., Šrámek, R. & Widmayer, P. Approximately Counting Approximately-Shortest Paths in Directed Acyclic Graphs. Theory Comput Syst 58, 45–59 (2016). https://doi.org/10.1007/s00224-014-9571-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00224-014-9571-7

Keywords