Skip to main content

Advertisement

Springer Nature Link
Log in

Effective investment to reduce lost-sales rate in a periodic review inventory model

  • Regular Article
  • Published:
OR Spectrum Aims and scope Submit manuscript

Abstract

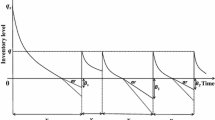
In 1973 Montgomery et al. proposed an (R, T) type of a periodic review inventory model in which the lost-sales rate caused by stockout is given. The purpose of this article is to investigate in this heuristic periodic review inventory model with partial lost-sales to effectively increase investment and to reduce the lost-sales rate. We discuss two models: complete (normal distribution) and partial (distribution free) information about the protection interval (i.e., review period plus lead time) demand distribution. For each model, two commonly used investment cost functional forms, logarithmic and power, are employed for lost-sales rate reduction. That is, for these two investment cost functions, we first assume that the protection interval demand follows a normal distribution, and then we assume that only first and second moments of the probability distribution of protected interval demand are known. Two algorithms are developed to find the optimal investment decision, and six numerical examples are given to illustrate the results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Donaldson WA (1984) An equation for the optimal value of T, the inventory replenishment review period when demand is normal. J Oper Res Soc 35(2):137–139

    Article  Google Scholar 

  • Gallego G, Moon I (1993) The distribution free newsboy problem: review and extensions. J Oper Res Soc 44:825–834

    Article  Google Scholar 

  • Hadley G, Whitin T (1963) Analysis of inventory systems. Prentice-Hall, New Jersey

    Google Scholar 

  • Hall RW (1983) Zero inventory. Dow Jones-Irwin, Homewood

    Google Scholar 

  • Hariga M, Ben-Daya M (1999) Some stochastic inventory models with deterministic variable lead time. Eur J Oper Res 113:42–51

    Article  Google Scholar 

  • Kim SL, Hayya JC, Hong JD (1992) Setup reduction in economic production quantity model. Decis Sci 23:500–508

    Article  Google Scholar 

  • Montgomery DC, Bazaraa MS, Keswani AK (1973) Inventory models with a mixture of backorders and lost sales. Nav Res Logist 20:255–263

    Article  Google Scholar 

  • Moon I, Choi S (1995) The distribution free newsboy problem with balking. J Oper Res Soc 46:537–542

    Article  Google Scholar 

  • Moon I, Choi S (1997) Distribution free procedures for mark-to-order (MTO), make-in-advance (MIA), and composite policies. Int J Prod Econ 48:21–28

    Article  Google Scholar 

  • Moon I, Choi S (1998) A note on lead time and distributional assumptions in continuous review inventory models. Comput Oper Res 25:1007–1012

    Article  Google Scholar 

  • Moon I, Silver E (2000) The multi-item newsvendor problem with a budget constraint and fixed ordering costs. J Oper Res Soc 51:602–608

    Article  Google Scholar 

  • Nasri F, Affisco JF, Paknejad MJ (1990) Setup cost reduction in an inventory model with finite-range stochastic lead times. Int J Prod Res 28:199–212

    Article  Google Scholar 

  • Ouyang LY, Chang HC (2001) The effects of investing in lost sales reduction on the stochastic inventory models. J Inf Optim Sci 22:357–368

    Google Scholar 

  • Ouyang LY, Chuang BR (2001) A periodic review inventory-control system with variable lead time. Int J Inf Manage Sci 12:1–13

    Google Scholar 

  • Ouyang LY, Yeh NC, Wu KS (1996) Mixture inventory model with backorders and lost sales for variable lead time. J Oper Res Soc 47:829–832

    Article  Google Scholar 

  • Paknejad MJ, Nasri F, Affisco JF (1995) Defective units in a continuous review (s, Q) system. Int J Prod Res 33(10):2767–2777

    Article  Google Scholar 

  • Porteus EL (1985) Investing in reduced setups in the EOQ model. Manage Sci 31:998–1010

    Article  Google Scholar 

  • Scarf H (1958) A min max solution of an inventory problem. In: Arrow KJ, Karlin S, Scarf H (eds) Studies in the mathematical theory of inventory and production. Stanford University Press, Stanford, CA, pp 201–209

    Google Scholar 

  • Silver E, Moon I (2001) The multi-item single period problem with an initial stock of convertible units. Eur J Oper Res 132:466–477

    Article  Google Scholar 

  • Silver EA, Pyke DF, Peterson R (1998) Inventory management and production planning and scheduling, 3rd edn. Wiley, New York

    Google Scholar 

  • Taylor BW III (1999) Introduction to management science, 6th edn. Prentice-Hall, NJ

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate Institute of Management Sciences, Tamkang University, Tamsui, Taipei Hsien, 251, Taiwan

    Liang-Yuh Ouyang

  2. Information and Communication Research Division, Chung-Shan Institute of Science and Technology, Lung-Tan, Tao-Yuan, Taiwan

    Bor-Ren Chuang

  3. Holistic Education Center, St. John’s University, Tamsui, Taipei, Taiwan

    Yu-Jen Lin

Authors
  1. Liang-Yuh Ouyang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bor-Ren Chuang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yu-Jen Lin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Liang-Yuh Ouyang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ouyang, LY., Chuang, BR. & Lin, YJ. Effective investment to reduce lost-sales rate in a periodic review inventory model. OR Spectrum 29, 681–697 (2007). https://doi.org/10.1007/s00291-007-0081-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00291-007-0081-8

Keywords