Abstract
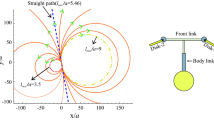
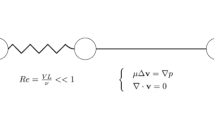
Swimming, i.e., being able to advance in the absence of external forces by performing cyclic shape changes, is particularly demanding at low Reynolds numbers. This is the regime of interest for micro-organisms and micro- or nano-robots. We focus in this paper on a simple yet representative example: the three-sphere swimmer of Najafi and Golestanian (Phys. Rev. E, 69, 062901–062904, 2004). For this system, we show how to cast the problem of swimming in the language of control theory, prove global controllability (which implies that the three-sphere swimmer can indeed swim), and propose a numerical algorithm to compute optimal strokes (which turn out to be suitably defined sub-Riemannian geodesics).
Similar content being viewed by others
References
Agrachev, A., Sachkov, Y.: Control theory from the geometric viewpoint. In: Control Theory and Optimization. Encyclopaedia of Mathematical Sciences, vol. 87. Springer, New York (2004)
Avron, J.E., Kenneth, O., Oakmin, D.H.: Pushmepullyou: An efficient micro-swimmer. New J. Phys. 7, 234–238 (2005)
Batchelor, G.K.: Brownian diffusion of particles with hydrodynamic interactions. J. Fluid Mech. 74, 1–29 (1976)
Becker, L.E., Koehler, S.A., Stone, H.A.: On self-propulsion of micro-machines at low Reynolds numbers: Purcell’s three-link swimmer. J. Fluid Mech. 490, 15–35 (2003)
Berg, H.C., Anderson, R.: Bacteria swim by rotating their flagellar filaments. Nature 245, 380–382 (1973)
Bressan, A.: Impulsive control of Lagrangian systems and locomotion in fluids. Preprint (2006)
Dautray, R., Lions, J.-L.: Mathematical Analysis and Numerical Methods for Science and Technology, vol. 4. Springer, Berlin (1990)
Golestanian, R.: personal communication to ADS (2006)
Kanso, E., Marsden, J.E., Rowley, C.W., Melli-Huber, J.B.: Locomotion of articulated bodies in a perfect fluid. J. Nonlinear Sci. 15, 255–289 (2005)
Koiller, J., Ehlers, K., Montgomery, R.: Problems and progress in microswimming. J. Nonlinear Sci. 6, 507–541 (1996)
Leshansky, A.M., Kenneth, O., Gat, O., Avron, J.E.: A frictionless microswimmer. Preprint (2007)
Lighthill, M.J.: On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Math. 5, 109–118 (1952)
Montgomery, R.: A Tour of Subriemannian Geometries, Their Geodesics and Applications. AMS Mathematical Surveys and Monographs, vol. 91. AMS, Providence (2002)
Morrey, C.B., Niremberg, L.: On the analyticity of the solutions of linear elliptic systems of partial differential equations. Commun. Pure Appl. Math. 10, 271–290 (1957)
Najafi, A., Golestanian, R.: Simple swimmer at low Reynolds numbers: Three linked spheres. Phys. Rev. E 69, 062901–062904 (2004)
Purcell, E.M.: Life at low Reynolds numbers. Am. J. Phys. 45, 3–11 (1977)
Taylor, G.I.: Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A 209, 447–461 (1951)
Wilkening, J., Hosoi, A.E.: Shape optimization of swimming sheets. Preprint (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Alouges, F., DeSimone, A. & Lefebvre, A. Optimal Strokes for Low Reynolds Number Swimmers: An Example. J Nonlinear Sci 18, 277–302 (2008). https://doi.org/10.1007/s00332-007-9013-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-007-9013-7
Keywords
- Biological and artificial micro-swimmers
- Optimal control
- Optimal gait
- Propulsion efficiency
- Movement and locomotion
- Low-Reynolds-number (creeping) flow