Skip to main content
SpringerLink
Log in

Dynamics of Phase Transitions in a Piecewise Linear Diatomic Chain

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

Abstract

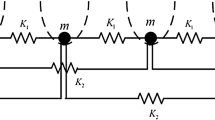
We consider a diatomic chain with nearest neighbors connected by phase-transforming springs. Assuming a piecewise linear interaction force, we use the Fourier transform to construct exact traveling wave solutions representing a moving phase-transition front and examine their stability through numerical experiments. We find that the identified traveling wave solutions may be stable in some velocity intervals. We show that the kinetic relation between the driving force on the phase boundary and its velocity is significantly affected by the ratio of the two masses. When the ratio is small enough, the relation may become multivalued at some velocities, with the two solutions corresponding to the different orders in which the two springs in a dimer cell change phase. The model bears additional interesting waveforms such as the so-called twinkling phase, which is also briefly discussed and compared to its monatomic analog.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abeyaratne, R., Knowles, J.K.: Kinetic relations and the propagation of phase boundaries in solids. Arch. Ration. Mech. Anal. 114, 119–154 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  • Atkinson, W., Cabrera, N.: Motion of a Frenkel–Kontorova dislocation in a one-dimensional crystal. Phys. Rev. A 138(3), 763–766 (1965)

    Google Scholar 

  • Balk, A.M., Cherkaev, A.V., Slepyan, L.I.: Dynamics of chains with non-monotone stress–strain relations I. Model and numerical experiments. J. Mech. Phys. Solids 49, 131–148 (2001a)

    Article  MathSciNet  MATH  Google Scholar 

  • Balk, A.M., Cherkaev, A.V., Slepyan, L.I.: Dynamics of chains with non-monotone stress–strain relations II. Nonlinear waves and waves of phase transition. J. Mech. Phys. Solids 49, 149–171 (2001b)

    Article  MathSciNet  MATH  Google Scholar 

  • Bilz, H., Büttner, H., Bussmann-Holder, A., Kress, W., Schröder, U.: Nonlinear lattice dynamics of crystals with structural phase transitions. Phys. Rev. Lett. 48(4), 264–267 (1982)

    Article  Google Scholar 

  • Boechler, N., Theocharis, G., Job, S., Kevrekidis, P.G., Porter, M.A., Daraio, C.: Discrete breathers in one-dimensional diatomic granular crystals. Phys. Rev. Lett. 104, 244302 (2010)

    Article  Google Scholar 

  • Brillouin, L.: Wave Propagation in Periodic Structures. Dover, New York (1953)

    MATH  Google Scholar 

  • Campbell, D.K., Rosenau, P., Zaslavsky, G.: Introduction: The Fermi–Pasta–Ulam problem—the first fifty years. Chaos 15(1), 015101 (2005)

    Article  Google Scholar 

  • Carpio, A., Bonilla, L.L.: Depinning transitions in discrete reaction-diffusion equations. SIAM J. Appl. Math. 63(3), 1056–1082 (2003a)

    Article  MathSciNet  MATH  Google Scholar 

  • Carpio, A., Bonilla, L.L.: Oscillatory wave fronts in chains of coupled nonlinear oscillators. Phys. Rev. E 67, 056621 (2003b)

    Article  MathSciNet  Google Scholar 

  • Celli, V., Flytzanis, N.: Motion of a screw dislocation in a crystal. J. Appl. Phys. 41(11), 4443–4447 (1970)

    Article  Google Scholar 

  • Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Springer, Heidelberg (2000)

    MATH  Google Scholar 

  • Earmme, Y.Y., Weiner, J.H.: Dislocation dynamics in the modified Frenkel–Kontorova model. J. Appl. Phys. 48(8), 3317–3331 (1977)

    Article  Google Scholar 

  • Fáth, G.: Propagation failure of traveling waves in discrete bistable medium. Physica D 116, 176–190 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  • Fleischer, J., Bartal, G., Cohen, O., Schwartz, T., Manela, O., Freedman, B., Segev, M., Buljan, H., Efremidis, N.: Spatial photonics in nonlinear waveguide arrays. Opt. Express 13(6), 1780–1796 (2005)

    Article  Google Scholar 

  • Flytzanis, N.: The dynamics of a diatomic chain on a parabolic substrate. Phys. Lett. A 85(6–7), 353–355 (1981)

    Article  Google Scholar 

  • Flytzanis, N., Celli, V., Nobile, A.: Motion of two screw dislocations in a lattice. J. Appl. Phys. 45(12), 5176–5181 (1974)

    Article  Google Scholar 

  • Flytzanis, N., Crowley, S., Celli, V.: High velocity dislocation motion and interatomic force law. J. Phys. Chem. Solids 38, 539–552 (1977)

    Article  Google Scholar 

  • Ford, J.: The Fermi–Pasta–Ulam problem: Paradox turns discovery. Phys. Rep. 213(5), 271–310 (1992)

    Article  MathSciNet  Google Scholar 

  • Ishioka, S.: Uniform motion of a screw dislocation in a lattice. J. Phys. Soc. Jpn. 30, 323–327 (1971)

    Article  Google Scholar 

  • James, G., Kastner, M.: Bifurcations of discrete breathers in a diatomic Fermi–Pasta–Ulam chain. Nonlinearity 20(3), 631–657 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  • Kivshar, Y.S., Agrawal, G.P.: Optical Solitons: From Fibers to Photonic Crystals. Academic Press, San Diego (2003)

    Google Scholar 

  • Kresse, O., Truskinovsky, L.: Mobility of lattice defects: discrete and continuum approaches. J. Mech. Phys. Solids 51, 1305–1332 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  • Kresse, O., Truskinovsky, L.: Lattice friction for crystalline defects: from dislocations to cracks. J. Mech. Phys. Solids 52, 2521–2543 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  • Lahiri, A., Panda, S., Roy, T.K.: Discrete breathers: exact solutions in piecewise linear models. Phys. Rev. Lett. 84(16), 3570–3573 (2000)

    Article  Google Scholar 

  • LeFloch, P.G.: Hyperbolic Systems of Conservation Laws. ETH Lecture Note Series. Birkhauser, Basel (2002)

    Book  MATH  Google Scholar 

  • Livi, R., Spicci, M., MacKay, R.S.: Breathers on a diatomic FPU chain. Nonlinearity 10(6), 1421–1434 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  • Marder, M., Gross, S.: Origin of crack tip instabilities. J. Mech. Phys. Solids 43, 1–48 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  • Mishuris, G.S., Movchan, A.B., Slepyan, L.I.: Localization and dynamic defects in lattice structures. In: Silberschmidt, V.V. (ed.) Computational and Experimental Mechanics of Advanced Materials. CISM Courses and Lectures, vol. 514, pp. 51–82. Springer, Berlin (2009)

    Chapter  Google Scholar 

  • Morsch, O., Oberthaler, M.: Dynamics of Bose–Einstein condensates in optical lattices. Rev. Mod. Phys. 78(1), 179–215 (2006)

    Article  Google Scholar 

  • Musgrave, M.J.P., Tasi, J.: Shock waves in diatomic chains I. Linear analysis. J. Mech. Phys. Solids 24, 19–42 (1976)

    Article  MathSciNet  Google Scholar 

  • Peyrard, M.: Nonlinear dynamics and statistical physics of DNA. Nonlinearity 17, R1–R40 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  • Rice, M.J., Mele, E.J.: Elementary excitations of a linearly conjugated diatomic polymer. Phys. Rev. Lett. 49(19), 1455–1459 (1982)

    Article  Google Scholar 

  • Rosakis, P., Vainchtein, A.: (2011, in preparation)

  • Sato, M., Hubbard, B.E., Sievers, A.J.: Colloquium: Nonlinear energy localization and its manipulation in micromechanical oscillator arrays. Rev. Mod. Phys. 78, 137 (2006)

    Article  Google Scholar 

  • Serre, D.: Systems of Conservation Laws, vol. 1. Cambridge University Press, Cambridge (1999a)

    Book  MATH  Google Scholar 

  • Serre, D.: Systems of Conservation Laws, vol. 2. Cambridge University Press, Cambridge (1999b)

    Book  MATH  Google Scholar 

  • Slepyan, L.I.: Dynamics of a crack in a lattice. Sov. Phys. Dokl. 26(5), 538–540 (1981)

    MATH  Google Scholar 

  • Slepyan, L.I.: Models and Phenomena in Fracture Mechanics. Springer, New York (2002)

    MATH  Google Scholar 

  • Slepyan, L.I., Troyankina, L.V.: Fracture wave in a chain structure. J. Appl. Mech. Tech. Phys. 25(6), 921–927 (1984)

    Article  Google Scholar 

  • Slepyan, L.I., Troyankina, L.V.: Impact waves in a nonlinear chain. In: Gol’dstein, R.V. (ed.) Plasticity and Fracture of Solids, pp. 175–186. Nauka, Moscow (1988) (in Russian)

    Google Scholar 

  • Slepyan, L.I., Cherkaev, A., Cherkaev, E.: Transition waves in bistable structures. II. Analytical solution: wave speed and energy dissipation. J. Mech. Phys. Solids 53, 407–436 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  • Sukhorukov, A.A., Kivshar, Y.S.: Discrete gap solitons in modulated waveguide arrays. Opt. Lett. 27(23), 2112–2114 (2002)

    Article  Google Scholar 

  • Trofimov, E., Vainchtein, A.: Kinks vs shocks in a discrete model of displacive phase transitions. Contin. Mech. Thermodyn. 22(5), 317–344 (2010)

    Article  MathSciNet  Google Scholar 

  • Truskinovsky, L.: Dynamics of nonequilibrium phase boundaries in a heat conducting elastic medium. J. Appl. Math. Mech. 51, 777–784 (1987)

    Article  MathSciNet  Google Scholar 

  • Truskinovsky, L.: Kinks versus shocks. In: Dunn, E., Fosdick, R., Slemrod, M. (eds.) Shock Induced Transitions and Phase Structures in General Media. IMA, vol. 52, pp. 185–229. Springer, Berlin (1993)

    Chapter  Google Scholar 

  • Truskinovsky, L., Vainchtein, A.: Explicit kinetic relation from “first principles”. In: Steinmann, P., Maugin, G.A. (eds.) Mechanics of Material Forces, pp. 43–50. Springer, Berlin (2005a)

    Chapter  Google Scholar 

  • Truskinovsky, L., Vainchtein, A.: Kinetics of martensitic phase transitions: Lattice model. SIAM J. Appl. Math. 66, 533–553 (2005b)

    Article  MathSciNet  MATH  Google Scholar 

  • Truskinovsky, L., Vainchtein, A.: Dynamics of martensitic phase boundaries: discreteness, dissipation and inertia. Contin. Mech. Thermodyn. 20(2), 97–122 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  • Vainchtein, A.: The role of spinodal region in the kinetics of lattice phase transitions. J. Mech. Phys. Solids 58(2), 227–240 (2009)

    Article  MathSciNet  Google Scholar 

  • Vainchtein, A.: Effect of nonlinearity on the steady motion of a twinning dislocation. Physica D 239, 1170–1179 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  • Vainchtein, A., Van Vleck, E.S.: Nucleation and propagation of phase mixtures in a bistable chain. Phys. Rev. B 79(14), 144123 (2009)

    Article  Google Scholar 

  • Zhen, Y., Vainchtein, A.: Dynamics of steps along a martensitic phase boundary I: Semi-analytical solution. J. Mech. Phys. Solids 56(2), 496–520 (2008a)

    Article  MathSciNet  MATH  Google Scholar 

  • Zhen, Y., Vainchtein, A.: Dynamics of steps along a martensitic phase boundary II: Numerical simulations. J. Mech. Phys. Solids 56(2), 521–541 (2008b)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Pittsburgh, Pittsburgh, PA, 15260, USA

    Anna Vainchtein

  2. Department of Mathematics and Statistics, University of Massachusetts, Amherst, MA, 01003, USA

    Panayotis G. Kevrekidis

Authors
  1. Anna Vainchtein
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Panayotis G. Kevrekidis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anna Vainchtein.

Additional information

Communicated by P. Newton.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vainchtein, A., Kevrekidis, P.G. Dynamics of Phase Transitions in a Piecewise Linear Diatomic Chain. J Nonlinear Sci 22, 107–134 (2012). https://doi.org/10.1007/s00332-011-9110-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00332-011-9110-5

Keywords

Mathematics Subject Classification (2000)

Search

Navigation