The Quenching Set of a MEMS Capacitor in Two-Dimensional Geometries

Abstract

The formation of finite time singularities in a nonlinear parabolic fourth order partial differential equation (PDE) is investigated for a variety of two-dimensional geometries. The PDE is a variant of a canonical model for Micro–Electro Mechanical systems (MEMS). The singularities are observed to form at specific points in the domain and correspond to solutions whose values remain finite but whose derivatives diverge as the finite time singularity is approached. This phenomenon is known as quenching. An asymptotic analysis reveals that the quenching set can be predicted by simple geometric considerations suggesting that the phenomenon described is generic to higher order parabolic equations which exhibit finite time singularity.

Appendices

Appendix A: Numerical Method

Numerical simulations of (2) with boundary condition (1b) were performed in MATLAB, with a finite element method. The domain Ω is approximated by a mesh consisting of triangular cells, the size of which can be spatially adapted to maintain numerical accuracy in regions where touchdown occurs. This is done by means of two consecutive simulations. In the first simulation, an estimate of the location of the touchdown points is obtained. The grid is then refined several times around those points, using a newest-vertex-bisection (NVB) rule (Traxler 1997) on the set of elements that are close to these first estimates of touchdown points. A refined triangle with one sweep of the NVB method has an area of roughly 1/2 or 1/4 of the original element. The simulation is then run again on the refined grid. Time stepping is performed dynamically to guarantee accuracy close to touchdown.

We assume we have defined a triangulation $\mathcal{T}_{h}$ of a two-dimensional polygonal domain $\tilde{\varOmega}$ that approximates Ω, in addition to the space V _h of $\mathbb{P}_{1}$ finite elements which vanish on $\partial \tilde{\varOmega}$:

$$V_h = \bigl\{ u_h \in \mathcal{C}(\varOmega) \bigm| u_h|_{\partial\tilde{\varOmega}}=0, \ u_h|_T \in \mathbb{P}_1,\ \forall T\in \mathcal{T}_h \bigr\}, $$

where $\mathbb{P}_{1}$ is the set of bivariate linear polynomials. A basis of V _h is easily constructed by numbering the set of vertices of the triangulation {p ₁,…,p _J } and considering the functions φ _i ∈V _h such that φ _i (p _j )=δ _ij . Associated to these functions, we can construct the stiffness matrix (which is the natural approximation of the −Δ operator with Dirichlet boundary conditions)

$${S}_{ij}=\int_\varOmega \nabla \varphi_i\cdot\nabla\varphi_j \, \mathrm{d}x, $$

and the lumped mass matrix

$${M}_{ij}=\delta_{ij}\int_\varOmega \varphi_i \, \mathrm{d}x. $$

As an approximation of Δ², we will consider the matrix

$$\boldsymbol{\Delta}_2:=\mathbf{SM}^{-1}\mathbf{S}, $$

which is sparse, symmetric, positive definite and relatively easy to compute. This discretisation is a slight variant of the bi-Laplacian approximation of Ciarlet and Raviart (1974) (the original method uses the full mass matrix instead of its lumped approximation, making the matrix Δ ₂ not directly computable). This method also appeared in Ishihara (1978) quoting Miyoshi (1972) as the original source, but its approximation properties were only recently clarified in the very detailed analysis of Arnold et al. (2012).

There are several reasons to use low order elements. First of all, we are working on a polyhedral approximation of the boundary, which makes the use of higher order elements suboptimal. The alternative option of using isoparametric elements is quite expensive. Secondly, the lumped mass matrix that we use in the approximation of the bi-Laplacian is a key element to have a completely computed approximation of the bi-Laplacian (as opposed to having an algorithm requiring a linear solve as part of the matrix–vector multiplication process). Mass lumping has the right order of convergence for linear elements but it is suboptimal for higher order elements (it is very often used for explicit time-stepping, where suboptimality is not relevant, but the mass matrix plays an important role in approximation of the operator here). For a steady state clamped bi-Laplacian problem on a convex or smooth domain, the current method has order two in the L ² norm. A higher order method is only attainable with better boundary approximation and avoiding mass lumping, which makes it impossible to have a fully assembled matrix approximation of the bi-Laplacian.

To approximate u(x,t), we first assume that we have constructed a sequence of time steps

$$0=t_0<t_1<t_2 <\cdots < t_n < \cdots $$

and we let δ _n :=t _n+1−t _n . We approximate $u(\cdot,t_{n})\approx u_{h}^{n}\in V_{h}$ for all n≥0 and we identify $u_{h}^{n}$ with its set of coefficients $\mathbf{u}^{n}:=(u^{n}_{1},\ldots,u^{n}_{J})$ so that

$$u_h^n=\sum_{j=1}^J u^n_j\varphi_j, \quad u^n_j=u_h(\mathbf{p}_j,t_n) \approx u(\mathbf{p}_j,t_n). $$

Discretisation of the parabolic equation

$$\partial_t u+\varepsilon^2 \Delta^2 u + \phi(u)=0, \quad \phi(u):=\frac{1}{(1+u)^2} $$

with homogeneous Dirichlet (clamped) boundary conditions

$$u|_{\partial\varOmega}=\partial_n u|_{\partial\varOmega}=0 \quad \forall t $$

is carried out using a Crank–Nicholson scheme for the linear part, a 2-step Adams–Bashforth scheme for the non-linear term, with lumped mass approximation of the identity operator in space and pointwise interpolation of the function ϕ. A time-step of the resulting method can be described as

$$\frac{1}{\delta_n}\mathbf {M} \bigl(\mathbf{u}^{n+1}-\mathbf{u}^n \bigr) +\frac{\varepsilon^2}{2}\boldsymbol{\Delta}_2 \bigl( \mathbf{u}^{n+1}+\mathbf{u}^n \bigr)+(1+q_n)\mathbf {M} \boldsymbol{\phi}\bigl(\mathbf{u}^n \bigr) -q_n\mathbf {M} \boldsymbol{\phi}\bigl(\mathbf{u}^{n-1} \bigr)=\mathbf{0} \quad n\ge \!1, $$

where in this equation we have employed the notation

$$q_n=\frac{\delta_n}{2\delta_{n-1}}, \qquad \boldsymbol{\phi}(\mathbf{v})_i=\phi(v_i). $$

Note that M is a diagonal matrix. Its effect on the time-stepping system can be understood as a rescaling of the equations to take into account the sizes of the elements around nodal points. A variational formulation of (2) would lead to a sparse non-diagonal mass matrix: the lumped mass version that we are using concentrates the values of the elements of the exact mass matrix in the diagonal, thus making its inversion straightforward. For the first time step, we apply a simple predictor–corrector strategy, first using a Taylor approximation that is further corrected with a linearly implicit Crank–Nicholson step. Starting at u(⋅,0)≡0, since ∂ _t u(⋅,0)≡−ϕ(0)=−1, the approximation u(⋅,t ₁)≈−δ ₀ can be discretized by constructing the vector $\mathbf{u}^{1}_{\circ}=-\delta_{0} (1,\ldots,1)$. This first guess is then corrected with

$$\frac{1}{\delta_0}\mathbf {M}\mathbf{u}^1+\frac{\varepsilon^2}{2} \boldsymbol{\Delta}_2\mathbf{u}^1+\frac{1}{2}\mathbf {M} \bigl( \boldsymbol{\phi}\bigl(\mathbf{u}^1_\circ \bigr)+\boldsymbol{\phi}( \mathbf{0}) \bigr)=\mathbf{0}. $$

The matrices

$$\frac{\mathbf {M}}{\delta_n} + \frac{\varepsilon ^2}{2}\boldsymbol{\Delta}_2 $$

are sparse, symmetric, positive definite. The time-stepping strategy is complemented with a dynamic choice of the time step (Budd and Williams 2010). Given a starting parameter δ _τ , we construct

$$\delta_n:=\delta_\tau g \bigl(\mathbf{u}^n \bigr), \quad \mbox{where} \ g(\mathbf{v}):=\min_j | 1+v_j|^3. $$

Note that this is the result of a forward Euler discretisation at fixed time-step δ _τ of the equation

$$\frac{\mathrm{d} t}{\mathrm{d}\tau}=\min_{ x\in \varOmega} \bigl|1+u(x,t)\bigr|^3, $$

preceding the implicit time-stepping method for the associated PDE. Integration is carried out until

$$\min_j u^{n+1}_j <-1+ \delta_{\mathrm{tol}} $$

for a predetermined tolerance δ _tol.

Appendix B: Local Behaviour Near Touchdown

This appendix is concerned with the asymptotic profile of the solution near touchdown. The discussion below follows that developed in Lindsay and Lega (2012) for touchdown at the origin, in the case of two-dimensional radially symmetric solutions. For more general treatments of singularity formation in higher order PDEs, the reader is referred to Galaktionov and Williams (2003), Bernoff et al. (1998), Bernoff and Witelski (1999, 2010), Galaktionov (2009), Budd et al. (2004) and the references therein.

In the vicinity of a touchdown point $x_{\mathrm{c}} \in \mathbb{R}^{2}$, we seek solutions in terms of the similarity variables

$$ u(x,t) = -1 + (t_\mathrm{c}-t)^{1/3}v(\eta,s), \quad \eta = \frac{x-x_\mathrm{c}}{\varepsilon ^{1/2}(t_\mathrm{c}-t)^{1/4}}, \ s= -\log|t_\mathrm{c}-t|. $$

(29)

By substituting (29) into (2), the following equation for v(η,s) is obtained:

(30a)

(30b)

The far field behaviour (30b) arises from the condition that $u_{t} = \mathcal{O}(1)$ far from x _c, as $t\to t_{\mathrm{c}}^{-}$. The touchdown profile of (2) as $t\to t_{\mathrm{c}}^{-}$ is thus given by the solution of (30a), (30b) in the limit s→∞ for fixed η. To investigate the existence of self-similar solutions, i.e. those satisfying v _s →0 as s→∞, we consider the time independent problem

(31a)

(31b)

The existence and multiplicity of symmetric and asymmetric solutions to (31a), (31b) is a challenging open question. Additionally, the stability of any solutions to (31a), (31b) under dynamics (30a), (30b) must be addressed. If one seeks a radially symmetric solution to (31a), (31b) in terms of a single variable r=|η|, then (31a), (31b) reduces to

(32a)

(32b)

Numerical simulations (cf. Lindsay and Lega 2012) of (32a), (32b) suggest the existence of precisely two profiles $\bar{v}_{1}(r)$ and $\bar{v}_{2}(r)$, of which only $\bar{v}_{1}(r)$, shown as a dashed curve in Fig. 15(d), is dynamically stable. It is therefore expected that if the touchdown profile is self-similar and radially symmetric, it should locally be given by the solution $\bar{v}_{1}(r)$. We remark that the existence of precisely two self-similar profiles has also been observed (cf. Galaktionov and Williams 2003; Budd et al. 2004) in related higher order finite time singularity problems.

Fig. 15

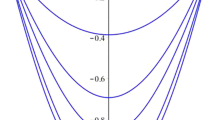
Comparison of asymptotic predictions with full numerics of (2) with ε=0.05 on the ellipse. In (a), the numerical solution of (2) for t _c−t=9.357×10⁻¹⁰ is shown with refinement in regions where 1+u(x,t) is close to 0. In (b), an enlargement of the solution profile in the vicinity of the touchdown point is shown. The minimum is attained at (x _c1,x _c2)=(0.5702,0.0002) with a corresponding value u(x _c1,x _c2)=−0.999. (c) shows the contours of the solution in the vicinity of the touchdown point with the ratio σ of major to minor axis for the best-fit ellipse (cf. Fitzgibbon et al. 1999) overlaid. This ratio appears to be approaching 1 as (x ₁,x ₂)→(x _c1,x _c2) indicating that solutions are represented by a radially symmetric function close to touchdown. In (d), solution profiles (solid) taken radially through the touchdown point are compared with the stable radially symmetric self-similar profile $\bar{v}_{1}(\eta)$ (dashed) satisfying (32a), (32b). Good agreement is observed

We now numerically investigate the validity of this assumption in the case of touchdown in the elliptical domain of Sect. 3.3, given by

$$\biggl(\frac{x_1}{a} \biggr)^2 + \biggl(\frac{x_2}{b} \biggr)^2 \leq 1; \quad a = 1.5, \ b = 0.75. $$

For our comparison, the value ε=0.05 is used and the solution of (2) is numerically advanced until min _x∈Ω u(x,t)=−0.999. From (29), we expect the touchdown profile to satisfy the asymptotic relationship

$$ \min_{x\in\varOmega} \bigl(1+u(x,t) \bigr)^3\propto(t_\mathrm{c}-t) $$

(33)

as $t\to t_{\mathrm{c}}^{-}$. As a consequence, the touchdown time t _c can be accurately estimated by finding the intercept of a linear fit between min _x∈Ω (1+u(x,t))³ and t with the horizontal axis. Indeed, this linear fit is found to be very good with a residual value of r=−0.999998 and a resulting touchdown time of t _c=0.311028113536382. This good agreement suggests that there are no logarithmic corrections to the quenching rate in this problem, however, such corrections in blow-up/quenching rates are notoriously difficult to rigorously establish and numerically verify, as for instance was discussed in Lindsay and Lega (2012), Budd and Williams (2010).

In this example, the solution u is minimum at two distinct points located on the horizontal axis and symmetrically about the origin, as shown in Fig. 15(a–b). The touchdown point (x _c1,x _c2)∼(0.57,0.0) is isolated for comparison with the self-similar profile $\bar{v}_{1}(r)$. The contours of the solution are seen to approach circles as (x ₁,x ₂)→(x _c1,x _c2), as shown in Fig. 15(c). This suggests the limiting profile near touchdown is radially symmetric. Indeed, good agreement is observed between $\bar{v}_{1}(r)$ and the numerical solution (cf. Fig. 15(d)). A refined numerical study of the dynamics of (2) very close to the singularity would be necessary to confirm the self-similar nature of the touchdown profile. However, this is beyond the scope of the present work and of the numerical method employed in this article.