Nonconstant Positive Steady States and Pattern Formation of 1D Prey-Taxis Systems

Abstract

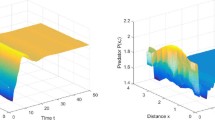
Prey-taxis is the process that predators move preferentially toward patches with highest density of prey. It is well known to have an important role in biological control and the maintenance of biodiversity. To model the coexistence and spatial distributions of predator and prey species, this paper concerns nonconstant positive steady states of a wide class of prey-taxis systems with general functional responses over 1D domain. Linearized stability of the positive equilibrium is analyzed to show that prey-taxis destabilizes prey–predator homogeneity when prey repulsion (e.g., due to volume-filling effect in predator species or group defense in prey species) is present, and prey-taxis stabilizes the homogeneity otherwise. Then, we investigate the existence and stability of nonconstant positive steady states to the system through rigorous bifurcation analysis. Moreover, we provide detailed and thorough calculations to determine properties such as pitchfork and turning direction of the local branches. Our stability results also provide a stable wave mode selection mechanism for thee reaction–advection–diffusion systems including prey-taxis models considered in this paper. Finally, we provide numerical studies of prey-taxis systems with Holling–Tanner kinetics to illustrate and support our theoretical findings. Our numerical simulations demonstrate that the $2\times 2$ prey-taxis system is able to model the formation and evolution of various striking patterns, such as spikes, periodic oscillations, and coarsening even when the domain is one-dimensional. These dynamics can model the coexistence and spatial distributions of interacting prey and predator species. We also give some insights on how system parameters influence pattern formation in these models.

Appendix

In this Appendix, we determine the direction of the pitchfork branch $\Gamma _{k}(s)$ for system (3.1) with general population kinetics. According to Theorem 4.2 and Corollary 1, the only stable local branch must be $\Gamma _{k_0}(s)$, $s\in (-\delta ,\delta )$, and its stability is determined by the turning direction, while all the rest are always unstable. We see that each bifurcation branch $\Gamma _{k}$ turns to the right if $\mathcal K_2>0$ and it turns to the left if $\mathcal K_2<0$. Therefore, we shall need to evaluate the sign of $\mathcal K_2$ in order to determine the stability of the stationary solution to (1.1).

Our calculations apply for each $k\in \mathbb N^+$, and in order to evaluate $\mathcal {K}_2$, we proceed as follows. By the asymptotic expansions (4.1)–(4.4), we equate $s^3$-terms in the second equation of (3.1)

$$\begin{aligned}&d_2\psi ''_2+\bar{g}_u\varphi _2+\bar{g}_v\psi _2\nonumber \\&\qquad +\left( \bar{g}_{uu}+\bar{g}_{uv} Q_k \right) \varphi _1\cos \frac{k\pi x}{L}+\left( \bar{g}_{uv}+\bar{g}_{vv} Q_k \right) \psi _1\cos \frac{k\pi x}{L}\nonumber \\&\qquad +\frac{1}{6}\left( \bar{g}_{uuu}+3\bar{g}_{uuv} Q_k+3\bar{g}_{uvv} Q^2_k+\bar{g}_{vvv} Q^3_k \right) \cos ^3\frac{k\pi x}{L}\nonumber \\&\quad =\chi _k\left( \bar{\phi }\varphi ''_2 +\left( \bar{\phi }_u+\bar{\phi }_v Q_k \right) \left( \varphi '_1\cos \frac{k\pi x}{L}\right) ' +\bar{\phi }_u \left( \varphi _1\cos '\frac{k\pi x}{L}\right) '\right. \nonumber \\&\qquad +\bar{\phi }_v\left( \psi _1\cos '\frac{k\pi x}{L}\right) '\nonumber \\&\qquad \left. +\frac{1}{2}\left( \bar{\phi }_{uu}+2\bar{\phi }_{uv} Q_k+\bar{\phi }_{vv} Q^2_k \right) \left( \cos ^2\frac{k\pi x}{L}\cos '\frac{k\pi x}{L}\right) '\right) \nonumber \\&\qquad +\mathcal {K}_2\bar{\phi }\cos ''\frac{k\pi x}{L}. \end{aligned}$$

(6.1)

In order to obtain closed formula of $\mathcal K_2$, we collect the following identities which can be easily obtained through straightforward calculations,

$$\begin{aligned}&\left\{ \begin{array}{ll} \int _0^L\varphi _1\cos ^2\frac{k\pi x}{L}\hbox {d}x=\frac{1}{2}\int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x+\frac{1}{2}\int _0^L\varphi _1\hbox {d}x, \\ \int _0^L\psi _1\cos ^2\frac{k\pi x}{L}\hbox {d}x=\frac{1}{2}\int _0^L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x+\frac{1}{2}\int _0^L\psi _1\hbox {d}x, \end{array} \right. \end{aligned}$$

(6.2)

$$\begin{aligned}&\left\{ \begin{array}{ll} \int _0^L\left( \varphi '_1\cos \frac{k\pi x}{L}\right) '\cos \frac{k\pi x}{L}\hbox {d}x=-\left( \frac{k\pi }{L}\right) ^2\int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x,\\ \int _0^L\left( \varphi _1\cos '\frac{k\pi x}{L}\right) '\cos \frac{k\pi x}{L}\hbox {d}x=\frac{1}{2}\left( \frac{k\pi }{L}\right) ^2 \left( \int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x-\int _0^L\varphi _1\hbox {d}x \right) ,\\ \int _0^L\left( \psi _1\cos '\frac{k\pi x}{L}\right) '\cos \frac{k\pi x}{L}\hbox {d}x=\frac{1}{2}\left( \frac{k\pi }{L}\right) ^2 \left( \int _0^L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x-\int _0^L\psi _1\hbox {d}x \right) , \end{array} \right. \nonumber \\ \end{aligned}$$

(6.3)

and

$$\begin{aligned} \left\{ \begin{array}{ll} \int _0^L\cos ^4\frac{k\pi x}{L}\hbox {d}x=\frac{3}{8}L,\\ \int _0^L\left( \cos ^2\frac{k\pi x}{L}\cos '\frac{k\pi x}{L}\right) '\cos \frac{k\pi x}{L}\hbox {d}x=-\frac{k^2\pi ^2}{8L}. \end{array} \right. \end{aligned}$$

(6.4)

Multiplying (6.1) by $\cos \frac{k\pi x}{L}$ and integrating it over (0, L) by parts, we conclude from (6.2)–(6.4) that

$$\begin{aligned} \mathcal {K}_2&=-\frac{2L}{\bar{\phi }(k\pi )^2}\left( A_1\int _0^L\varphi _2\cos \frac{k\pi x}{L}\hbox {d}x+A_2\int _0^L\psi _2\cos \frac{k\pi x}{L}\hbox {d}x+A_3\int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x\right. \nonumber \\&\left. \qquad +A_4\int _0^L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x+A_5\int _0^L\varphi _1\hbox {d}x+A_6\int _0^L\psi _1\hbox {d}x+A_7\right) , \end{aligned}$$

(6.5)

where we denote

$$\begin{aligned} A_1= & {} \chi _k\bar{\phi }\left( \frac{k\pi }{L}\right) ^2+\bar{g}_u, A_2=-d_2\left( \frac{k\pi }{L}\right) ^2+\bar{g}_v,\\ A_3= & {} \frac{1}{2}(\bar{g}_{uu}+\bar{g}_{uv} Q_k)+\chi _k\left( \frac{1}{2}\bar{\phi }_u+\bar{\phi }_v Q_k\right) \left( \frac{k\pi }{L}\right) ^2,\\ A_4= & {} \frac{1}{2}\left( \bar{g}_{uv}+\bar{g}_{vv} Q_k \right) -\frac{1}{2}\chi _k\bar{\phi }_v\left( \frac{k\pi }{L}\right) ^2,\\ A_5= & {} \frac{1}{2}\left( \bar{g}_{uu}+\bar{g}_{uv} Q_k \right) +\frac{1}{2}\chi _k\bar{\phi }_u\left( \frac{k\pi }{L}\right) ^2,\\ A_6= & {} \frac{1}{2}\left( \bar{g}_{uv}+\bar{g}_{vv} Q_k \right) +\frac{1}{2}\chi _k\bar{\phi }_v\left( \frac{k\pi }{L}\right) ^2, \end{aligned}$$

and

$$\begin{aligned} A_7= & {} \frac{L}{16}\left( \left( \bar{g}_{uuu}+3\bar{g}_{uuv} Q_k+3\bar{g}_{uvv} Q^2_k+\bar{g}_{vvv} Q^3_k \right) \right. \\&\left. +\chi _k\left( \frac{k\pi }{L}\right) ^2\left( \bar{\phi }_{uu}+2\bar{\phi }_{uv} Q_k+ \bar{\phi }_{vv} Q^2_k \right) \right) . \end{aligned}$$

Equating $s^3$-terms in the first equation of (3.1), we have that

$$\begin{aligned}&d_1\varphi ''_2+\bar{f}_u\varphi _2+\bar{f}_v\psi _2\nonumber \\&\quad +\left( \bar{f}_{uu} +\bar{f}_{uv} Q_k \right) \varphi _1\cos \frac{k\pi x}{L}+\left( \bar{f}_{uv} +\bar{f}_{vv} Q_k \right) \psi _1\cos \frac{k\pi x}{L}\nonumber \\&\quad +\frac{1}{6}\left( \bar{f}_{uuu}+3\bar{f}_{uuv} Q_k+3\bar{f}_{uvv} Q^2_k+\bar{f}_{vvv} Q^3_k\right) \cos ^3\frac{k\pi x}{L}=0. \end{aligned}$$

(6.6)

Multiplying (6.6) by $\cos \frac{k\pi x}{L}$ and integrating it over (0, L) lead us to

$$\begin{aligned} \left( -d_1\big (\frac{k\pi }{L}\big )^2+\bar{f}_u \right) \int _0^L \varphi _2 \cos \frac{k\pi x}{L}\hbox {d}x +\bar{f}_v\int _0^L \psi _2 \cos \frac{k\pi x}{L}\hbox {d}x =C_0, \end{aligned}$$

(6.7)

where

$$\begin{aligned} C_0=&-\frac{1}{2}\left( \bar{f}_{uu} +\bar{f}_{uv} Q_k \right) \int _0^L \varphi _1 \cos \frac{2k\pi x}{L}\hbox {d}x\\&-\frac{1}{2}\left( \bar{f}_{uv} +\bar{f}_{vv} Q_k \right) \int _0^L \psi _1 \cos \frac{2k\pi x}{L}\hbox {d}x\\&-\frac{1}{2}\left( \bar{f}_{uu} +\bar{f}_{uv} Q_k \right) \int _0^L \varphi _1\hbox {d}x -\frac{1}{2}\left( \bar{f}_{uv} +\bar{f}_{vv} Q_k \right) \int _0^L \psi _1\hbox {d}x\\&-\frac{L}{16}\left( \bar{f}_{uuu}+3\bar{f}_{uuv} Q_k+3\bar{f}_{uvv} Q^2_k+\bar{f}_{vvv} Q^3_k\right) . \end{aligned}$$

On the other hand, since $(\varphi _2,\psi _2)\in \mathcal {Z}$ as defined in (3.14), we have that

$$\begin{aligned} \bar{f}_v\int _0^L \varphi _2 \cos \frac{k\pi x}{L}\hbox {d}x +\left( d_1\left( \frac{k\pi }{L}\right) ^2-\bar{f}_u\right) \int _0^L \psi _2 \cos \frac{k\pi x}{L}\hbox {d}x =0. \end{aligned}$$

(6.8)

Combining (6.7) and (6.8) gives

$$\begin{aligned} \begin{pmatrix} -d_1\left( \frac{k\pi }{L}\right) ^2+\bar{f}_u &{} \bar{f}_v \\ \bar{f}_v &{} d_1\left( \frac{k\pi }{L}\right) ^2-\bar{f}_u \end{pmatrix} \begin{pmatrix} \int _0^L \varphi _2 \cos \frac{k\pi x}{L} \hbox {d}x \\ \int _0^L \psi _2 \cos \frac{k\pi x}{L} \hbox {d}x \end{pmatrix} = \begin{pmatrix} C_0 \\ 0 \end{pmatrix} \end{aligned}$$

(6.9)

and solving (6.9) gives

$$\begin{aligned} \int _0^L \varphi _2 \cos \frac{k\pi x}{L}\hbox {d}x =\frac{B_1}{B_0}, \int _0^L \psi _2 \cos \frac{k\pi x}{L}\hbox {d}x =\frac{B_2}{B_0}, \end{aligned}$$

(6.10)

where

$$\begin{aligned} B_0=-\left( d_1\left( \frac{k\pi }{L}\right) ^2-\bar{f}_u \right) ^2-\bar{f}^2_v, B_1=C_0\left( d_1\left( \frac{k\pi }{L}\right) ^2-\bar{f}_u \right) , B_2=-\bar{f}_v C_0. \end{aligned}$$

Finally, we need to evaluate $\int _0^L\varphi _1\hbox {d}x$, $\int _0^L\psi _1\hbox {d}x$, $\int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x$, and $\int _0^L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x$.

Integrating (4.5) and (4.7) over (0, L), we have that

$$\begin{aligned} \begin{pmatrix} \bar{f}_u &{} \bar{f}_v \\ \bar{g}_u &{} \bar{g}_v \end{pmatrix} \begin{pmatrix} \int _0^L\varphi _1\hbox {d}x \\ \int _0^L\psi _1\hbox {d}x \end{pmatrix} = \begin{pmatrix} -\frac{L}{4}\left( \bar{f}_{uu} +2\bar{f}_{uv} Q_k+\bar{f}_{vv} Q^2_k \right) \\ -\frac{L}{4}\left( \bar{g}_{uu} +2\bar{g}_{uv} Q_k+\bar{g}_{vv} Q^2_k \right) \end{pmatrix}. \end{aligned}$$

(6.11)

Solving (6.11) gives us

$$\begin{aligned} \int _0^L\varphi _1\hbox {d}x =\frac{D_1}{D_0}, \int _0^L\psi _1\hbox {d}x =\frac{D_2}{D_0}, \end{aligned}$$

(6.12)

where

$$\begin{aligned} D_0= & {} \bar{f}_u\bar{g}_v-\bar{f}_v\bar{g}_u,\\ D_1= & {} -\frac{L}{4}\left( \left( \bar{f}_{uu} +2\bar{f}_{uv} Q_k+\bar{f}_{vv} Q^2_k \right) \bar{g}_v-\left( \bar{g}_{uu} +2\bar{g}_{uv} Q_k+\bar{g}_{vv} Q^2_k \right) \bar{f}_v\right) ,\\ D_2= & {} \frac{L}{4}\left( \left( \bar{f}_{uu} +2\bar{f}_{uv} Q_k+\bar{f}_{vv} Q^2_k \right) \bar{g}_u-\left( \bar{g}_{uu} +2\bar{g}_{uv} Q_k+\bar{g}_{vv} Q^2_k \right) \bar{f}_u\right) . \end{aligned}$$

Multiplying (4.5) and (4.7) by $\cos \frac{2k\pi x}{L}$ and then integrating them over (0, L) by part, we have that

$$\begin{aligned} \begin{pmatrix} -d_1\left( \frac{2k\pi }{L}\right) ^2+\bar{f}_u&{}\bar{f}_v \\ \chi _k \bar{\phi }\left( \frac{2k\pi }{L}\right) ^2+\bar{g}_u&{} -d_2\left( \frac{2k\pi }{L}\right) ^2+\bar{g}_v \end{pmatrix} \begin{pmatrix} \int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x\\ \int _0^L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x \end{pmatrix} = \begin{pmatrix} C_3 \\ C_4 \end{pmatrix}. \end{aligned}$$

(6.13)

where

$$\begin{aligned} C_3= & {} -\frac{L}{8}\left( \bar{f}_{uu} +2\bar{f}_{uv} Q_k+\bar{f}_{vv} Q^2_k \right) ,\\ C_4= & {} -\frac{L}{8}\left( \bar{g}_{uu} +2\bar{g}_{uv} Q_k+\bar{g}_{vv} Q^2_k \right) -\frac{k^2\pi ^2}{2L}\chi _k \left( \bar{\phi }_u+\bar{\phi }_v Q_k \right) . \end{aligned}$$

Solving (6.13) gives us

$$\begin{aligned} \int ^0_L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x =\frac{E_1}{E_0}, \int ^0_L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x =\frac{E_2}{E_0}, \end{aligned}$$

(6.14)

where

$$\begin{aligned} E_0= & {} \left( -d_1\left( \frac{2k\pi }{L}\right) ^2+\bar{f}_u \right) \left( -d_2\left( \frac{2k\pi }{L}\right) ^2+\bar{g}_v \right) -\left( \chi _k \bar{\phi }\big (\frac{2k\pi }{L}\big )^2+\bar{g}_u \right) \bar{f}_v,\\ E_1= & {} C_3\left( -d_2\left( \frac{2k\pi }{L}\right) ^2+\bar{g}_v \right) -C_4\bar{f}_v, \end{aligned}$$

and

$$\begin{aligned} E_2=\left( -d_1\left( \frac{2k\pi }{L}\right) ^2+\bar{f}_u \right) C_4-\left( \chi _k \bar{\phi }\left( \frac{2k\pi }{L}\right) ^2+\bar{g}_u \right) C_3. \end{aligned}$$

We point out that $E_0$ is always nonzero thanks to (3.12).

In light of (6.10), (6.12), and (6.14), we are able to represent $\mathcal K_2$ in (6.5) in terms of system parameters.