Skip to main content
SpringerLink
Log in

Classification of \((n+1, 1)\)-Stacked Central Configurations in \(R^3\)

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

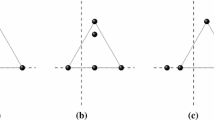
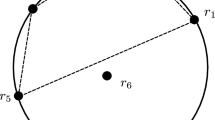
Abstract

We classify the extensions of n-body central configurations to \((n+1)\)-body central configurations in \(R^3\), in both the collinear case and the non-collinear case. We completely solve the two open questions posed by Hampton (Nonlinearity 18: 2299-2304, 2005). This classification is related with study on co-circular and co-spherical central configurations. We also obtain a general property of co-circular central configurations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

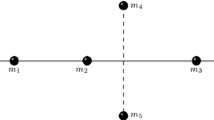
  1. According to Theorem 1, there is no five-body collinear central configuration with a subset forming a four-body central configuration.

References

  • Albouy, A.: On a paper of moeckel on central configurations. Regul. Chaotic Dyn. 8(2), 133–142 (2003)

    Article  MathSciNet  Google Scholar 

  • Albouy, A., Cabral, H.E., Santos, A.A.: Some problems on the classical N-body problem. Celestial Mech. Dynam. Astronom. 113(4), 369–375 (2012)

    Article  MathSciNet  Google Scholar 

  • Albouy, A., Kaloshin, V.: Finiteness of central configurations of five bodies in the plane. Ann. Math. 176(1), 535–588 (2012)

    Article  MathSciNet  Google Scholar 

  • Alvarez-Ramírez, M., Santos, A.A., Vidal, C.: On co-circular central configurations in the four and five body-problems for homogeneous force law. J. Dynam. Differ. Equ. 25(2), 269–290 (2013)

    Article  MathSciNet  Google Scholar 

  • Chen, Kuo-Chang, Hsiao, Jun-Shian: Strictly convex central configurations of the planar five-body problem. Trans. Am. Math. Soc. 370(3), 1907–1924 (2018)

    Article  MathSciNet  Google Scholar 

  • Chenciner, A.: Are There Perverse Choreographies? New Advances in Celestial Mechanics and Hamiltonian Systems, pp. 63–76. Kluwer/Plenum, New York (2004)

    Book  Google Scholar 

  • Corbera, M., Llibre, J., Pérez-Chavela, Ernesto: Spatial Bi-stacked central configurations formed by two dual regular polyhedra. J. Math. Anal. Appl. 413(2), 648–659 (2014)

    Article  MathSciNet  Google Scholar 

  • Cors, J.M., Roberts, G.E.: Four-body co-circular central configurations. Nonlinearity 25(2), 343–370 (2012)

    Article  MathSciNet  Google Scholar 

  • Euler, L.: De motu rectilineo trium corporum se mutuo attrahentium. Novi Commun. Acad. Sci. Imp. Petrop. 11, 144–151 (1767)

    Google Scholar 

  • Fayçal, N.: On the classification of pyramidal central configurations. Proc. Am. Math. Soc. 124(1), 249–258 (1996)

    Article  MathSciNet  Google Scholar 

  • Fernandes, A.C., Mello, L.F.: On stacked planar central configurations with five bodies when one body is removed. Qual. Theory Dyn. Syst. 12(2), 293–303 (2013)

    Article  MathSciNet  Google Scholar 

  • Fernandes, A.C., Mello, L.F.: On stacked planar central configurations with \(n\) bodies when one body is removed. J. Math. Anal. Appl. 405(1), 320–325 (2013)

    Article  MathSciNet  Google Scholar 

  • Fernandes, A.C., Mello, L.F.: Rigidity of planar central configurations. Z. Angew. Math. Phys. 66(6), 2979–2994 (2015)

    Article  MathSciNet  Google Scholar 

  • Fernandes, A.C., Mello, L.F.: Correction to: On stacked planar central configurations with five bodies when one body is removed. Qual. Theory Dyn. Syst. (2018). https://doi.org/10.1007/s12346-018-0280-5

  • Hampton, M.: Co-Circular Central Configurations in the Four-Body Problem, EQUADIFF 2003, 993–998. World Science Publications, Hackensack, NJ (2005)

  • Hampton, M.: Stacked central configurations: New examples in the planar five-body problem. Nonlinearity 18(5), 2299–2304 (2005)

    Article  MathSciNet  Google Scholar 

  • Hampton, M., Santoprete, M.: Seven-body central configurations: A family of central configurations in the spatial seven-body problem. Celestial Mech. Dynam. Astronom. 99(4), 293–305 (2007)

    Article  MathSciNet  Google Scholar 

  • Lagrange, J.L.: Essai sur le Problème des Trois Corps. Œuvres tome 6, 229–332 (1772)

    Google Scholar 

  • Llibre, J., Moeckel, R., Simó, C.: Central Configurations, Periodic Orbits, and Hamiltonian Systems. Advanced Courses in Mathematics, CRM Barcelona, Birkhäuser/Springer, Basel (2015)

  • Moeckel, R.: On central configurations. Math. Z. 205(4), 499–517 (1990)

    Article  MathSciNet  Google Scholar 

  • MacMillan, W.D., Bartky, M.: Permanent configurations in the problem of four bodies. Trans. Am. Math. Soc. 34(4), 838–875 (1932)

    Article  MathSciNet  Google Scholar 

  • Moeckel, R., Simó, C.: Bifurcation of spatial central configurations from planar ones. SIAM J. Math. Anal. 26(4), 978–998 (1995)

    Article  MathSciNet  Google Scholar 

  • Oliveira, A., Cabral, H.: On stacked central configurations of the planar coorbital satellites problem. Discrete Contin. Dyn. Syst. 32(10), 3715–3732 (2012)

    Article  MathSciNet  Google Scholar 

  • Ouyang, T., Xie, Z., Zhang, S.: Pyramidal Central Configurations and Perverse Solutions. Electron. J. Differ. Equ. (106), 9 p (2004)

  • Saari, D.: On the role and properties of central configurations. Celestial Mech. 21, 9–20 (1980)

    Article  MathSciNet  Google Scholar 

  • Smale, S.: Topology and mechanics, II. the planar \(N\)-body problem. Invent. Math. 11, 45–64 (1970)

    Article  MathSciNet  Google Scholar 

  • Zhang, S., Zhou, Q.: Double pyramidal central configurations. Phys. Lett. A 281(4), 240–248 (2001)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Xiang Yu was supported by NSFC (No. 11701464) and the Fundamental Research Funds for the Central Universities (No. JBK1805001). Shuqiang Zhu was supported by NSFC (No. 11801537, No. 11721101) and the Fundamental Research Funds for the Central Universities (No. WK0 010450010).

Author information

Authors and Affiliations

  1. School of Economic and Mathematics, Southwestern University of Finance and Economics, Chengdu, 611130, People’s Republic of China

    Xiang Yu & Shuqiang Zhu

Authors
  1. Xiang Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuqiang Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuqiang Zhu.

Additional information

Communicated by Jeff Moehlis.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, X., Zhu, S. Classification of \((n+1, 1)\)-Stacked Central Configurations in \(R^3\). J Nonlinear Sci 31, 11 (2021). https://doi.org/10.1007/s00332-020-09659-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00332-020-09659-0

Keywords

Search

Navigation