Abstract
A quasi-one-dimensional Poisson–Nernst–Planck system for ionic flow through a membrane channel is studied. Nonzero but small permanent charge, the major structural quantity of an ion channel, is included in the model. The system includes three ion species, two cations with the same valences and one anion, which provides more correlations/interactions between ions compared to the case included only two oppositely charged particles. The cross-section area of the channel is included in the system, which provides certain information of the geometry of the three-dimensional channel. This is crucial for our analysis. Under the framework of geometric singular perturbation theory, more importantly, the specific structure of the model, the existence and local uniqueness of solutions to the system for small permanent charges is established. Furthermore, treating the permanent charge as a small parameter, through regular perturbation analysis, we are able to derive approximations of the individual fluxes explicitly, and this allows us to examine the small permanent charge effects on ionic flows in detail. Of particular interest is the competition between two cations, which is related to the selectivity phenomena of ion channels. Critical potentials are identified and their roles in characterizing ionic flow properties are studied. Some critical potentials can be estimated experimentally, and this provides an efficient way to adjust/control boundary conditions (electric potential and concentrations) to observe distinct qualitative properties of ionic flows. Mathematical analysis further indicates that to optimize the effect of permanent charges, a short and narrow filter, within which the permanent charge is confined, is expected, which is consistent with the typical structure of an ion channel.

Similar content being viewed by others
References
Abaid, N., Eisenberg, R.S., Liu, W.: Asymptotic expansions of I–V relations via a Poisson–Nernst–Planck system. SIAM J. Appl. Dyn. Syst. 7, 1507–1526 (2008)
Aitbayev, R., Bates, P.W., Lu, H., Zhang, L., Zhang, M.: Mathematical studies of Poisson–Nernst–Planck systems: dynamics of ionic flows without electroneutrality conditions. J. Comput. Appl. Math. 362, 510–527 (2019)
Barcilon, V.: Ion flow through narrow membrane channels: part I. SIAM J. Appl. Math. 52, 1391–1404 (1992)
Barcilon, V., Chen, D.-P., Eisenberg, R.S.: Ion flow through narrow membrane channels: part II. SIAM J. Appl. Math. 52, 1405–1425 (1992)
Barcilon, V., Chen, D.-P., Eisenberg, R.S., Jerome, J.W.: Qualitative properties of steady-state Poisson–Nernst–Planck systems: perturbation and simulation study. SIAM J. Appl. Math. 57, 631–648 (1997)
Bates, P.W., Chen, J., Zhang, M.: Dynamics of ionic flows via Poisson–Nernst–Planck systems with local hard-sphere potentials: competition between cations. Math. Biosci. Eng. 17, 3736–3766 (2020)
Bates, P.W., Jia, Y., Lin, G., Lu, H., Zhang, M.: Individual flux study via steady-state Poisson–Nernst–Planck systems: effects from boundary conditions. SIAM J. Appl. Dyn. Syst. 16(1), 410–430 (2017)
Biesheuvel, P.M.: Two-fluid model for the simultaneous flow of colloids and fluids in porous media. J. Colloid Interface Sci. 355, 389–395 (2011)
Boda, D., Nonner, W., Valisko, M., Henderson, D., Eisenberg, B., Gillespie, D.: Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys. J. 93, 1960–1980 (2007)
Chen, D., Eisenberg, R., Jerome, J., Shu, C.: Hydrodynamic model of temperature change in open ionic channels. Biophys. J. 69, 2304–2322 (1995)
Eisenberg, B.: Ion channels as devices. J. Comp. Electron. 2, 245–249 (2003)
Eisenberg, B.: Proteins, channels, and crowded ions. Biophys. Chem. 100, 507–517 (2003)
Eisenberg, R.S.: Channels as enzymes. J. Memb. Biol. 115, 1–12 (1990)
Eisenberg, R.S.: Atomic biology, electrostatics and ionic channels. In: Elber, R. (ed.) New Developments and Theoretical Studies of Proteins, pp. 269–357. World Scientific, Philadelphia (1996)
Eisenberg, B.: Crowded charges in ion channels. In: Rice, S.A. (ed.) Advances in Chemical Physics, pp. 77–223. Wiley, Hoboken (2011)
Eisenberg, B., Hyon, Y., Liu, C.: Energy variational analysis of ions in water and channels: field theory for primitive models of complex ionic fluids. J. Chem. Phys. 133(104104), 1–23 (2010)
Eisenberg, B., Liu, W.: Poisson-Nernst-Planck systems for ion channels with permanent charges. SIAM J. Math. Anal. 38, 1932–1966 (2007)
Eisenberg, B., Liu, W.: Relative dielectric constants and selectivity ratios in open ionic channels. Mol. Based Math. Biol. 5, 125–137 (2017)
Eisenberg, B., Liu, W., Xu, H.: Reversal charge and reversal potential: case studies via classical Poisson–Nernst–Planck models. Nonlinearity 28, 103–128 (2015)
Fair, J.C., Osterle, J.F.: Reverse Electrodialysis in charged capillary membranes. J. Chem. Phys. 54, 3307–3316 (1971)
Fenichel, N.: Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31, 53–98 (1979)
Gillespie, D.: Energetics of divalent selectivity in a calcium channel: the Ryanodine receptor case study. Biophys. J. 94, 1169–1184 (2008)
Gillespie, D., Eisenberg, R.S.: Physical descriptions of experimental selectivity measurements in ion channels. Eur. Biophys. J. 31, 454–466 (2002)
Gillespie, D.: A singular perturbation analysis of the Poisson-Nernst-Planck system: Applications to Ionic Channels. Ph.D Dissertation, Rush University at Chicago (1999)
Gillespie, D., Nonner, W., Eisenberg, R.S.: Coupling Poisson–Nernst–Planck and density functional theory to calculate ion flux. J. Phys. Condens. Matter 14, 12129–12145 (2002)
Gillespie, D., Nonner, W., Eisenberg, R.S.: Crowded charge in biological ion channels. Nanotechnology 3, 435–438 (2003)
Gross, R.J., Osterle, J.F.: Membrane transport characteristics of ultra fine capillary. J. Chem. Phys. 49, 228–234 (1968)
Hodgkin, A.L., Keynes, R.D.: The potassium permeability of a giant nerve fibre. J. Physiol. 128, 61–88 (1955)
Hyon, Y., Eisenberg, B., Liu, C.: A mathematical model for the hard sphere repulsion in ionic solutions. Commun. Math. Sci. 9, 459–475 (2010)
Hyon, Y., Fonseca, J., Eisenberg, B., Liu, C.: Energy variational approach to study charge inversion (layering) near charged walls. Discrete Contin. Dyn. Syst. Ser. B 17, 2725–2743 (2012)
Hyon, Y., Liu, C., Eisenberg, B.: PNP equations with steric effects: a model of ion flow through channels. J. Phys. Chem. B 116, 11422–11441 (2012)
Im, W., Roux, B.: Ion permeation and selectivity of OmpF porin: a theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 322, 851–869 (2002)
Ji, S., Eisenberg, B., Liu, W.: Flux ratios and channel structures. J. Dyn. Differ. Equ. 31, 1141–1183 (2019)
Ji, S., Liu, W.: Poisson–Nernst–Planck systems for ion flow with density functional theory for hard-sphere potential: I–V relations and critical potentials: part I: analysis. J. Dyn. Differ. Equ. 24, 955–983 (2012)
Ji, S., Liu, W., Zhang, M.: Effects of (small) permanent charges and channel geometry on ionic flows via classical Poisson–Nernst–Planck models. SIAM J. Appl. Math. 75, 114–135 (2015)
Jia, Y., Liu, W., Zhang, M.: Qualitative properties of ionic flows via Poisson–Nernst–Planck systems with Bikerman’s local hard-sphere potential: ion size effects. Discrete Contin. Dyn. Syst. Ser. B 21, 1775–1802 (2016)
Jones, C.: Geometric singular perturbation theory. Dynamical systems (Montecatini Terme, 1994), pp. 44–118. Lect. Notes in Math. 1609, Springer, Berlin (1995)
Jones, C., Kopell, N.: Tracking invariant manifolds with differential forms in singularly perturbed systems. J. Differ. Equ. 108, 64–88 (1994)
Kilic, M.S., Bazant, M.Z., Ajdari, A.: Steric effects in the dynamics of electrolytes at large applied voltages: II: modified Poisson–Nernst–Planck equations. Phys. Rev. E 75, 021503 (2007)
Liu, J.L., Eisenberg, B.: Poisson–Nernst–Planck–Fermi theory for modeling biological ion channels. J. Chem. Phys. 141, 12B640 (2014)
Lee, C.-C., Lee, H., Hyon, Y., Lin, T.-C., Liu, C.: New Poisson–Boltzmann type equations: one-dimensional solutions. Nonlinearity 24, 431–458 (2011)
Lin, G., Liu, W., Yi, Y., Zhang, M.: Poisson–Nernst–Planck systems for ion flow with density functional theory for local hard-sphere potential. SIAM J. Appl. Dyn. Syst. 12, 1613–1648 (2013)
Liu, W.: Geometric singular perturbation approach to steady-state Poisson–Nernst–Planck systems. SIAM J. Appl. Math. 65, 754–766 (2005)
Liu, W.: One-dimensional steady-state Poisson–Nernst–Planck systems for ion channels with multiple ion species. J. Differ. Equ. 246, 428–451 (2009)
Liu, W., Wang, B.: Poisson–Nernst–Planck systems for narrow tubular-like membrane channels. J. Dyn. Differ. Equ. 22, 413–437 (2010)
Liu, W., Tu, X., Zhang, M.: Poisson–Nernst–Planck systems for ion flow with density functional theory for hard-sphere potential: I–V relations and critical potentials: part II: Numerics. J. Dyn. Differ. Equ. 24, 985–1004 (2012)
Liu, W., Xu, H.: A complete analysis of a classical Poisson–Nernst–Planck model for ionic flow. J. Differ. Equ. 258, 1192–1228 (2015)
Lu, H., Li, J., Shackelford, J., Vorenberg, J., Zhang, M.: Ion size effects on individual fluxes via Poisson–Nernst–Planck systems with Bikerman’s local hard-sphere potential: analysis without electroneutrality boundary conditions. Discrete Contin. Dyn. Syst. Ser. B 23, 1623–1643 (2018)
Nonner, W., Eisenberg, R.S.: Ion permeation and glutamate residues linked by Poisson–Nernst–Planck theory in L-type Calcium channels. Biophys. J. 75, 1287–1305 (1998)
Park, J.-K., Jerome, J.W.: Qualitative properties of steady-state Poisson–Nernst–Planck systems: mathematical study. SIAM J. Appl. Math. 57, 609–630 (1997)
Rouston, D.J.: Bipolar Semiconductor Devices. McGraw-Hill, New York (1990)
Roux, B., Allen, T.W., Berneche, S., Im, W.: Theoretical and computational models of biological ion channels. Q. Rev. Biophys. 37, 15–103 (2004)
Sasidhar, V., Ruckenstein, E.: Electrolyte osmosis through capillaries. J. Colloid Interface Sci. 82, 439–457 (1981)
Schuss, Z., Nadler, B., Eisenberg, R.S.: Derivation of Poisson and Nernst–Planck equations in a bath and channel from a molecular model. Phys. Rev. E 64, 1–14 (2001)
Singer, A., Norbury, J.: A Poisson–Nernst–Planck model for biological ion channels-an asymptotic analysis in a three-dimensional narrow funnel. SIAM J. Appl. Math. 70, 949–968 (2009)
Singer, A., Gillespie, D., Norbury, J., Eisenberg, R.S.: Singular perturbation analysis of the steady-state Poisson–Nernst–Planck system: applications to ion channels. Eur. J. Appl. Math. 19, 541–560 (2008)
Sun, L., Liu, W.: Non-localness of excess potentials and boundary value problems of Poisson–Nernst–Planck systems for ionic flow: a case study. J. Dyn. Differ. Equ. 30, 779–797 (2018)
Tin, S.-K., Kopell, N., Jones, C.: Invariant manifolds and singularly perturbed boundary value problems. SIAM J. Numer. Anal. 31, 1558–1576 (1994)
Warner, R.M., Jr.: Microelectronics: its unusual origin and personality. IEEE Trans. Electron. Dev. 48, 2457–2467 (2001)
Wang, X.-S., He, D., Wylie, J., Huang, H.: Singular perturbation solutions of steady-state Poisson–Nernst–Planck systems. Phys. Rev. E 89(022722), 1–14 (2014)
Wei, G.W.: Differential geometry based multiscale models. Bull. Math. Biol. 72, 1562–1622 (2010)
Wei, G.W., Zheng, Q., Chen, Z., Xia, K.: Variational multiscale models for charge transport. SIAM Rev. 54, 699–754 (2012)
Wen, Z., Zhang, L., Zhang, M.: Dynamics of classical Poisson–Nernst–Planck systems with multiple cations and boundary layers. J. Dyn. Differ. Equ. 33, 211–234 (2021)
Zhang, M.: Asymptotic expansions and numerical simulations of I–V relations via a steady-state Poisson–Nernst–Planck system. Rocky Mountain J. Math. 45, 1681–1708 (2015)
Zhang, M.: Boundary layer effects on ionic flows via classical Poisson–Nernst–Planck systems. Comput. Math. Biophys. 6, 14–27 (2018)
Acknowledgements
The authors are grateful to the anonymous referees whose suggestions have in our opinion, significantly improved the paper. Z. Wen thanks the Math Department at New Mexico Tech for the hospitality during his one-year visit to the department when the main part of this work is complete. Z. Wen is partially supported by China Scholarship Council, the National Natural Science Foundation of China (No. 12071162 and No. 11701191) and Fundamental Research Funds for the Central Universities (N0. ZQN-802). M. Zhang is supported by MPS Simons Foundation (No. 628308).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Arnd Scheel.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs of Some Results
Appendix: Proofs of Some Results
1.1 Proof of Proposition 2.3
We will provide a detailed proof for statement (i), and the second statement can be argued in a similar way. To get started, we assume
is a solution of the limiting fast system (2.3) from \(B_{j-1}\) to \({{\mathcal {Z}}}_j\); namely, \(z(\xi )\in N^{[j-1,r]}=M^{[j-1,r]}\cap W^s({{\mathcal {Z}}}_j)\). It follows that \(J_1(\xi ), J_2(\xi ), J_3(\xi )\) are constants and \(\tau (\xi )=x_{j-1}\). Notice that \(z(0)\in B_{j-1}\) and \(\lim _{\xi \rightarrow +\infty }z(\xi )=z(+\infty )\in {{\mathcal {Z}}}_j.\) One has \(\phi (0)=\phi ^{[j-1]},\ c_k(0)=c_k^{[j-1]}, \ u(+\infty )=0,\) and \(z_1c_1(+\infty )+z_2c_2(+\infty )+z_3c_3(+\infty )+Q_j=0.\) Define \(u(0)=u^{[j-1,r]}\). By the integrals in Proposition 2.2, we get
Hence,
Now the first two equations in the limiting fast system (2.3) read
which is a Hamiltonian system with a Hamiltonian function given by
Not difficult to see that the above Hamiltonian function is exactly the integral \(H_4\) in Proposition 2.2 with the relation (6.1). The equilibria of (6.2) are given by
We now claim that \(\phi ^{[j-1,r]}\) is the unique solution of the second equation in (6.3). To get started, we let
It is easy to see that \(f'(\phi )=-\sum _{k=1}^3z_k^2c_k^{[j-1]}e^{z_k\big (\phi ^{[j-1]}-\phi \big )}<0,\) which implies that \(f(\phi )\) is a decreasing function. Note that in our set-up, \(z_1>0,\ z_2>0,\ z_3<0\) and \(c_k^{[j-1]}\)’s are positive, one has \(f(\phi )\rightarrow -\infty \) as \(\phi \rightarrow +\infty \) and \(f(\phi )\rightarrow +\infty \) as \(\phi \rightarrow -\infty \). Correspondingly, (6.3) has a unique solution.
Let \(c_k(+\infty )=c_k^{[j-1,r]}\), then, from (6.1), one has \(c_k^{[j-1,r]}=c_k^{[j-1]}e^{-z_k\big (\phi ^{[j-1,r]}-\phi ^{[j-1]}\big )}.\) Evaluating the integral \(H_4\) in Proposition 2.2 at \(\xi =0\) and \(\xi \rightarrow +\infty \), we have
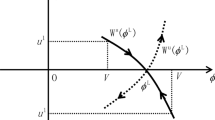
which gives the expression for \(u^{[j-1,r]}\). The choice of the sign can be determined from the phase portrait sketched in Fig. 2.
The phase portrait for the Hamiltonian system (6.2). The sign of \(u^{[j-1,r]}\) agrees with the sign of \(\phi ^{[j-1,r]}-\phi ^{[j-1]}\)
We now claim that the expressions under the square root in \(u^{[j-1,r]}\) and \(u^{[j,l]}\) are non-negative. We just provide the proof for the expression in \(u^{[j-1,r]}\). Let
Notice that \(F'(\phi )=f(\phi )\) and \(F''(\phi )=f'(\phi )\) where \(f(\phi )\) is defined in (6.4). Since \(f'(\phi )<0\), one has \(F(\phi )\) is concave down. Together with \(F'(\phi ^{[j-1,r]})=f(\phi ^{[j-1,r]})=0\), one has \(F(\phi ^{[j-1,r]})\) is the unique maximal value of \(F(\phi )\), and in particular, \(F(\phi ^{[j-1,r]})\ge F(\phi ^{[j-1]})=0.\)
Finally, we consider the transversal intersection of the stable manifold \(W^s(\mathcal {Z}_j)\) and \(B_{j-1}\) at points \(\big (\phi ^{[j-1]}, u^{[j-1,r]}, c_1^{[j-1]}, c_2^{[j-1]}, c_3^{[j-1]}, J_1, J_2, J_3, x_{j-1}\big ).\) From the above argument, they do intersect at the specified points, and one only need to verify the intersection is transversal. Since the stable manifold is completely characterized, one can compute its tangent space at each intersection point (via the complete set of first integrals obtained in Proposition 2.2) to verify the transversality of the intersection. It is slightly complicated but straightforward. We would like to omit the detail here. This completes the proof.
1.2 Proof of Proposition 2.8
Plugging (2.27) into (2.18), the zeroth-order system in \(Q_0\) reads
Recall that on \(\mathcal {Z}_j\), one has \(z_1c_1+z_2c_2+z_3c_3+Q_j=0\). Plugging (2.27) into it, the zeroth-order terms in \(Q_0\) gives
Plugging (6.6) into the first two equations of (6.5) gives
From (2.19), one then has
for \(k=1,2,3\), and further, from (6.5), we have
Adding \(J_{10},\ J_{20}\) and \(J_{30}\) in (6.7), together with the last equation in (6.7), one has
from which
which implies
and
It follows from the fifth equation in (6.7) that
Adding the first two equations in (6.7), one has
Equations (6.9), (6.10), (6.11), together with the fourth equation in (6.7) yield
It now follows that
From the first two equations and the penultimate equation in (6.7), one has
from which, one obtains the expressions of \(c_{10}^{[1]}, \ c_{20}^{[1]}, \ c_{10}^{[2]}\) and \(c_{20}^{[2]}\). The expressions for \(J_{10}\) and \(J_{20}\) then follow. This completes the proof.
1.3 Proof of Lemma 3.5
\(N>0\) follows from the fact that both M and \(\ln \frac{\omega (\beta )}{\omega (\alpha )}\) have the same sign with that of \(R-L\). Rewrite \(1-N\) as
One then can easily obtain \(\lim _{t\rightarrow 1}(1-N)=0\).
For the other statements, we just established statement (i) for \(t>1\), and those for \(t<1\) can be proved similarly. Direct computation yields \(\frac{\mathrm{d}(1-N)}{\mathrm{d} \beta }=\frac{g_{1}(\beta )}{(\beta -\alpha )^{2}(t-1)^{2}},\) where \(g_{1}(\beta )=-\omega ^{2}(\alpha )\ln t \ln \frac{\omega (\beta )}{\omega (\alpha )} +(\beta -\alpha )(t-1)^{2}\left( (\alpha -\gamma (t))\ln t-1\right) ,\) and further
It then follows that for \(t>1\), \(g_{1}(\beta )\) is concave upward. Furthermore, one has
which implies \(g_{1}(\beta )>0\) for \(\beta >\alpha \). Note that \(\displaystyle {\lim _{\beta \rightarrow \alpha }\frac{\mathrm{d}(1-N)}{\mathrm{d} \beta }=\ln \frac{t}{2}>0}\ \text{ for }\ t>1.\) We have \(\frac{\mathrm{d}(1-N)}{\mathrm{d} \beta }>0\) for \(\beta >\alpha \), and \(1-N\) is strictly increasing on \((\alpha ,+\infty )\). Additionally, since \(\displaystyle {\lim _{\beta \rightarrow \alpha }(1-N)=(\alpha -\gamma (t))\ln t,}\) one has, for \(t>1\),
-
(i1)
if \(\alpha \ge \gamma (t)\), then \(\frac{z}{z_{3}}<0<1-N\), which yields \(V_{1}<0<V_{2}\);
-
(i2)
For \(\alpha <\gamma (t)\), we first claim that there exists a unique \(\beta _{1}\in (\alpha ,1)\) such that \(1-N=0\) for \(\beta =\beta _{1}\). In fact, based on the facts that
$$\begin{aligned} \lim _{\beta \rightarrow \alpha }(1-N)=(\alpha -\gamma (t))\ln t<0\end{aligned}$$and \(1-N\) is strictly increasing on \((\alpha ,+\infty )\), one just need to show that \(1-N>0\) for \(\beta =1\), which is yielded by \(g(1)>0\). For convenience, for \(t>1\), we set
$$\begin{aligned} \begin{aligned} g_{2}(\alpha ):=g(1)=-\omega (\alpha )\ln t \ln \omega (\alpha )+(1-\alpha )(t-1)^{2}. \end{aligned} \end{aligned}$$Note that \(g_{2}''(\alpha )=-\frac{(1-t)^{2}\ln t}{\omega (\alpha )}<0\), which indicates that \(g_{2}(\alpha )\) is concave downward for \(t>1\). Note also that \(g_2(1)=0\). To show that \(g(1)>0\), we claim \(g_{2}(0)\ge 0\). To get started, we set
$$\begin{aligned} \begin{aligned} g_{3}(t):=g_{2}(0)=-t(\ln t)^{2}+(t-1)^{2}. \end{aligned} \end{aligned}$$Direct calculation gives \(g_{3}'(t)=-(\ln t)^{2}-2\ln t+2(t-1)\) and \(g_{3}''(t)=\frac{2}{t}(t-1-\ln t)>0\) for all \(t>1\). Together with \(g_{3}(1)=g_{3}'(1)=0\), one has \(g_{3}(t)=g_{2}(0)>0\).
If \(\alpha < \gamma (t)\) and \(\frac{z}{z_{3}}<(\alpha -\gamma (t))\ln t\), which is equivalent to \(\alpha< \gamma (t)<\alpha -\frac{z}{z_3\ln t}\), then, one has \(\frac{z}{z_{3}}<1-B\) for all \(\beta >\alpha \), and more specifically, \(\frac{z}{z_{3}}<1-N<0\), which implies \(V_{2}<V_{1}<0\) for \(\beta \in (\alpha ,\beta _{1})\); \(\frac{z}{z_{3}}<1-N=0\) for \(\beta =\beta _{1}\); \(\frac{z}{z_{3}}<0<1-N\), which indicates \(V_{1}<0<V_{2}\), for \(\beta \in (\beta _{1},1)\).
-
(i3)
if \( \gamma (t)>\alpha -\frac{z}{z_3\ln t}\), then, the straight line \(w=\frac{z}{z_{3}}\) and \(w=1-N\) have a unique intersection point \((\beta _{1}^{*}, w(\beta _{1}^{*}))\), which indicates that there exists a unique \(\beta _{1}^{*}\in (\alpha ,\beta _{1})\) such that \(1-N<\frac{z}{z_{3}}<0\), which suggests \(V_{1}<V_{2}<0\) for \(\beta \in (\alpha ,\beta _{1}^{*})\); \(1-N=\frac{z}{z_{3}}<0\) and further \(V_{2}=V_{1}<0\) for \(\beta =\beta _{1}^{*}\); \(\frac{z}{z_{3}}<1-N<0\), which yields \(V_{2}<V_{1}<0\) for \(\beta \in (\beta _{1}^{*},\beta _{1})\); \(\frac{z}{z_{3}}<1-N=0\) for \(\beta =\beta _{1}\); and \(\frac{z}{z_{3}}<0<1-N\), which indicates \(V_{1}<0<V_{2}\) for \(\beta \in (\beta _{1},1)\).
1.4 Proof of Theorem 3.18
where
It follows that
where \(g_{11}(V)=2\left( L_1-R_1e^{-zV}\right) +z\left( 2V-V_{1}-V_{2}\right) \left( L_1+R_1e^{-zV}\right) .\) For \(g_{11}(V)\), one has
From (6.13), we obtain a unique zero of \(g_{11}''(V)\) given by \(V_{0}=\frac{1}{2}\left( \frac{6}{z}+V_{1}+V_{2}\right) \), which is the minimum point of \(g_{11}'(V)\). Note that \(\displaystyle {\lim _{V\rightarrow +\infty }g_{11}'(V)=2zL_{1}>0}\) and \(\displaystyle {\lim _{V\rightarrow -\infty }g_{11}'(V)=+\infty .}\) If the minimal value \(g_{11}'(V_{0})=2z\left( L_{1}-R_{1}e^{-zV_{0}}\right) \ge 0\), i.e., \(V_{0}\le V_{3}\), then, \(g_{11}'(V)\le 0\) for all V. In this case, \(g_{11}(V)\) has a unique zero, since \(\displaystyle {\lim _{V\rightarrow +\infty }g_{11}(V)=+\infty } \) and \(\displaystyle {\lim _{V\rightarrow -\infty }g_{11}=-\infty .}\) If the minimal value \(g_{11}'(V_{0})=2z\left( L_{1}-R_{1}e^{-zV_{0}}\right) < 0\) i.e., \(V_{0}< V_{3}\), then \(g_{11}'(V)\) has two zeros. Suppose \(V_{e}\) is a zero point of \(g_{11}'(V)\), one has \(2V_{e}-V_{1}-V_{2}=\frac{4R_{1}+2L_{1}e^{zV_{e}}}{zR_{1}}\) and the extreme value of \(g_{11}(V)\) given by \(g_{11}(V_{e})=\frac{2}{R_{1}}\left( L_{1}^{2}e^{zV_{e}}+R_{1}^{2}e^{-zV_{e}} +4L_{1}R_{1}\right) >0,\) which indicates that \(g_{11}(V)\) has a unique zero point. Therefore, no matter \(V_{0}\le V_{3}\) or \(V_{0}< V_{3}\), \(g_{11}(V)\) always has a unique zero denoted by \(V_{z}\). Furthermore, \(f_{11}'(V)\) has two zeros \(V_{1}\) and \(V_{z}\). To determine the order of \(V_{1}\) and \(V_{z}\), one just need to determine the sign of \(g_{11}(V_{1})\). In fact, if \(g_{11}(V_{1})>0\), then \(V_{1}>V_{z}\), if \(g_{11}(V_{1})=0\), then \(V_{1}=V_{z}\), if \(g_{11}(V_{1})<0\), then \(V_{1}<V_{z}\).
Note that \(g_{11}(V_{1}) =\frac{1}{zL_{1}LR}\left[ C\frac{R_{1}}{L_{1}}+\frac{1}{(1-N)t}\Big (\frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)\Big )\right] ,\) where C is defined in (3.8) and the sign of the quantity C has been studied in Lemma 3.17. It then follows that , with \(\Delta =\frac{\frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)}{\frac{z}{z_{3}}\ln t-(\ln t+2)(1-N)},\)
-
for \(C>0\), one has \(g_{11}(V_{1})>0\) if \(\frac{R_1}{L_1}>-\frac{\Delta }{t}\), and \(g_{11}(V_{1})<0\) if \(\frac{R_1}{L_1}<-\frac{\Delta }{t}\).
-
for \(C<0\), one has \(g_{11}(V_{1})>0\) if \(\frac{R_1}{L_1}<-\frac{\Delta }{t}\), and \(g_{11}(V_{1})<0\) if \(\frac{R_1}{L_1}>-\frac{\Delta }{t}\).
-
for \(C=0\), one has \(g_{11}(V_{1})>0\).
In particular, \(g_{11}(V_{1})=0\) if \(\frac{R_1}{L_1}=-\frac{\Delta }{t}\) with \(C\ne 0\).
If \(V_{1}<V_{z}\), then \(f_{11}\) is increasing on \((-\infty , V_1)\), decreasing on \((V_{1},V_{2})\), and increasing on \((V_2,\infty )\). Note that \(f_{11}(V_{1})=0\), which is a local maximum of \(f_{11}\), \(\lim _{V\rightarrow -\infty }f_{11}=-\infty \) and \(\lim _{V\rightarrow \infty }f_{11}=\infty \), \(f_{11}\) has the other zero \(V_{11}^{1}\) with \(V_{11}^{1}>V_{1}\). Furthermore, \(\displaystyle {\lim _{V\rightarrow V_{1}}\frac{\mathrm{d}J_{11}}{\mathrm{d} V}=\frac{Mz_{3}(1-N)e^{zV_{1}}}{2(z-z_3)H(1)\left( \ln L-\ln R\right) ^{2}R}g_{11}(V_{1})<0,}\) since \(g_{11}(V_{1})<g_{11}(V_{z})=0\), which can be obtained from the fact that \(g_{11}\) is increasing on \((-\infty ,V_{z})\) and \(V_{1}<V_{z}\). Therefore, when \(V>V_{11}^{1}\), \(\frac{\mathrm{d}J_{11}}{\mathrm{d} V}>0\), and when \(V<V_{11}^{1}\), \(\frac{\mathrm{d}J_{11}}{\mathrm{d} V}<0\). This result also hold for the case when \(V_{1}\ge V_{z}\), which can be proved in a similar way. Consequently the statement (i) follows.
The statements for \(J_{21}\) and \(J_{31}\) can be proved similarly.
1.5 Proof of Theorem 4.6
We will just prove the first statement. Statement (ii) can be proved by a similar argument. For \(\frac{L_{2}}{L_{1}}<\frac{D_{1}}{D_{2}}<\frac{R_{2}}{R_{1}}\), one has
Direct calculation yields
and further
where \(f_{d3}(V)\) and \(g_{d3}(V)\) are given in (4.5).
For \(g_{d3}(V)\), we have
From (6.15), we obtain a unique zero of \(g_{d3}''(V)\) given by \(V_{0}=\frac{1}{2}\left( \frac{6}{z}+V_{1}+V_{2}\right) \), which actually is the maximum value point of \(g_{d3}'(V)\). Note that
and the maximal value \(g_{d3}'(V_{0})=2z\left( L_d^{-}-R_d^{-}e^{-zV_{0}}\right) > 0.\) Hence, \(g_{d3}'(V)\) has a unique zero denoted by \(V_{d3}\) and \(V_{d3}\) is actually the minimum value point of \(g_{d3}(V)\). From \(g_{d3}'(V)=0\), one immediately has \(2V_{d3}-V_{1}-V_{2}=\frac{4R_d^{-}+2L_d^{-}e^{zV_{d3}}}{zR_d^{-}}\) and the corresponding extreme value of \(g_{d3}(V)\), i.e., \(g_{d3}(V_{d3})=-\frac{2}{R_d^{-}}h(V_{d3})\). From lemma 4.5, \(g_{d3}(V_{d3})>0\) for \(V_{z}^{1}<V_{d3}<V_{z}^{2}\), \(g_{d3}(V_{d3})=0\) for \(V_{d3}=V_{z}^{1}\) or \(V_{d3}=V_{z}^{2}\), and \(g_{d3}(V_{d3})<0\) for \(V_{d3}<V_{z}^{1}\) or \(V_{d3}>V_{z}^{2}\).
If \(g_{d3}(V_{d3})>0\), then, \(g_{d3}(V)>0\) for all V. It follows that \(f_{d3}'(V)\) has a unique zero \(V_{1}\), \(f_{d3}'(V)>0\) for \(V>V_{1}\), and \(f_{d3}'(V)<0\) for \(V<V_{1}\). Therefore, the minimal value of \(f_{d3}(V)\) is \(f_{d3}(V_{1})=0\). Note that \(\displaystyle {\lim _{V\rightarrow V_{1}}\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}=\frac{Mz_{3}(1-N)g_{d3}(V_{1})}{2(z-z_3)H(1)\left( \ln L-\ln R\right) ^{2}L}>0.}\) Then, \(\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}>0\) follows, which yields \({{\mathcal {J}}}_{1,2}^1(V)\) always increases.
If \(g_{d3}(V_{d3})=0\), then \(g_{d3}(V)\) has the unique zero \(V_{d3}\). From (6.14), \(f_{d3}'(V)\) has two zeros \(V_{1}\) and \(V_{d3}\). To determine the position relation of \(V_{1}\) and \(V_{d3}\), one just need to determine the sign of \(g_{d3}'(V_{1})=2zR_d^{-}\bigg (\frac{L_d^{-}}{R_d^{-}}+\frac{t\big ((4+\ln t)(1-N)-\frac{z}{z_{3}}\ln t\big )}{2(1-N)}\bigg ).\) In fact, if \(g_{d3}'(V_{1})<0\), then \(V_{1}<V_{d3}\), if \(g_{d3}'(V_{1})=0\), then \(V_{1}=V_{d3}\), if \(g_{d3}'(V_{1})>0\), then \(V_{1}>V_{d3}\). However, no matter \(V_{1}<V_{d3}\) or \(V_{1}\ge V_{d3}\), from (6.14), one always has \(f_{d3}'\le 0\) for \(V<V_{1}\) and \(f_{d3}'\ge 0\) for \(V>V_{1}\). Hence, the minimal value of \(f_{d3}\) is \(f_{d3}(V_{1})=0\). Note that \(\displaystyle {\lim _{V\rightarrow V_{1}}\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}=\frac{Mz_{3}(1-N)g_{d3}(V_{1})}{2(z-z_3)H(1)\left( \ln L-\ln R\right) ^{2}L}>0.}\) Then, \(\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}>0\) follows, and hence, \({{\mathcal {J}}}_{1,2}^1(V)\) always increases.
If \(g_{d3}(V_{d3})<0\), then, \(g_{d3}(V)\) has two zeros denoted by \(V_{z}^{3}\) and \(V_{z}^{4}\) with \(V_{z}^{3}<V_{z}^{4}\), since \(\displaystyle {\lim _{V\rightarrow \pm \infty }g_{d3}=+\infty }\). It follows that \(f_{d3}'(V)\) has three zeros \(V_{1}\), \(V_{z}^{3}\) and \(V_{z}^{4}\). To determine the position relation of \(V_{1}\), \(V_{z}^{3}\) and \(V_{z}^{4}\), one just need to determine the sign of \(g_{d3}(V_{1})\) and \(g_{d3}'(V_{1})\). In fact, if \(g_{d3}(V_{1})<0\), then \(V_{z}^{3}<V_{1}<V_{z}^{4}\), if \(g_{d3}(V_{1})>0\) and \(g_{d3}'(V_{1})<0\), then \(V_{1}<V_{z}^{3}<V_{z}^{4}\), and if \(g_{d3}(V_{1})>0\) and \(g_{d3}'(V_{1})>0\), then \(V_{z}^{3}<V_{z}^{4}<V_{1}\).
Note that \(g_{d3}(V_{1})=\frac{\frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)}{(1-N)R_d^{-}}\bigg (\frac{L_d^{-}}{R_d^{-}}+\frac{1}{t\Delta }\bigg ).\) It follows that
-
For \(\frac{1}{1-N}\Big (\frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)\Big )>0\), one has \( g_{d3}(V_{1})>0\) (resp. \( g_{d3}(V_{1})<0\)) if \(\frac{L_d^{-}}{R_d^{-}}<-\frac{1}{t\Delta }\) (resp. \( \frac{L_d^{-}}{R_d^{-}}>-\frac{1}{t\Delta }\));
-
For \(\frac{1}{1-N}\left( \frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)\right) <0\), one has \(g_{d3}(V_{1})>0\) (resp. \(g_{d3}(V_{1})<0\)) if \(\frac{L_d^{-}}{R_d^{-}}>-\frac{1}{t\Delta }\) (resp. \(\frac{L_d^{-}}{R_d^{-}}<-\frac{1}{t\Delta }\));
-
For \(\frac{1}{1-N}\left( \frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)\right) \ne 0\), one has \(g_{d3}(V_{1})=0\) if \(\frac{L_d^{-}}{R_d^{-}}=-\frac{1}{t\Delta }\);
-
For \(\frac{1}{1-N}\left( \frac{z}{z_{3}}\ln t-(\ln t-2)(1-N)\right) =0\), one has \(g_{d3}(V_{1})>0\).
If \(V_{z}^{3}<V_{1}<V_{z}^{4}\), then, \(f_{d3}(V)\) decreases on \((-\infty , V_{z}^{3})\), increases on \((V_{z}^{3},V_{1})\), decreases on \((V_{1},V_{z}^{4})\), and increases on \((V_{z}^{4},\infty )\). Note that \(f_{d3}(V_{1})=0\), which is a local maximum of \(f_{d3}(V)\), one has \(f_{d3}(V_{z}^{3})<0\) and \(f_{d3}(V_{z}^{4})<0\). Since
\(\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}\) has two zeros denoted by \(V_{c}^{51}\) and \(V_{c}^{52}\) with \(V_{c}^{51}<V_{c}^{52}\) such that \(\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}>0\) for \(V<V_{c}^{51}\) or \(V>V_{c}^{52}\), and \(\frac{\mathrm{d}{{\mathcal {J}}}_{1,2}^1}{\mathrm{d} V}<0\) for \(V_{c}^{51}<V<V_{c}^{52}\), that is, \({{\mathcal {J}}}_{1,2}^1\) increases on \((-\infty , V_{c}^{51})\), decreases on \((V_{c}^{51},V_{c}^{52})\), and increases on \((V_{c}^{52},\infty )\).
Similar discussions can be applied to the cases with \(V_{1}<V_{z}^{3}<V_{z}^{4}\) and \(V_{z}^{3}<V_{z}^{4}<V_{1}\), respectively. This completes the proof of the first statement.
Rights and permissions
About this article
Cite this article
Bates, P.W., Wen, Z. & Zhang, M. Small Permanent Charge Effects on Individual Fluxes via Poisson–Nernst–Planck Models with Multiple Cations. J Nonlinear Sci 31, 55 (2021). https://doi.org/10.1007/s00332-021-09715-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-021-09715-3