Stability of Regular Polygonal Relative Equilibria on $\mathbf{}\mathbb S^2$

Abstract

For the regular polygonal relative equilibria on $\mathbb S^2$, we show that if all the particles are outside of the equator, then they are orbitally stable in a four-dimensional invariant symplectic manifold. For the stability in full space, if they are close to the north or south pole, then such relative equilibria are spectrally unstable. If they are close to the equator, then if the number of masses is odd, then they are orbitally stable; and if the number of masses is even, then they are spectrally unstable.

Appendix A. Positivity of \( \lambda _{ p + 1 } \)

This “Appendix” offers a numerical study of $\lambda _{ p+1 }$, supporting the claim that it is positive for all $n \ge 6$, n even. Recall that $\lambda _{ p + 1 }$ is given by (16), with $n = 2p + 2$. Thus, $\lambda _{ p + 1 } (\theta )$ is a continuous function of $\theta$ on the open interval $0< \theta < \pi / 2$.

Consider the family of algebraic functions $\mu _n (x)$, $x \in (0,1)$, defined by

$$\begin{aligned} \lambda _{ p + 1 } (\theta ) = \mu _{2(p+1)} (\cos ^2 \theta ) = \mu _n (\cos ^2 \theta ) \,. \end{aligned}$$

(That is to say, $\mu _n$ is obtained from the right-hand side of (16) substituting $\cos \theta$ with $\sqrt{x}$ and $\sin \theta$ with $\sqrt{1-x}$.) We want to determine the qualitative shape of $\mu _n (x)$. It turns out that $\mu _n (x)$ blows-up at the two ends of the interval (0, 1) ; indeed, $\mu _n (x)$ is $O(x ^{ -3/2 })$ near $x = 0$ and $O((1 - x) ^{ -3/2 })$ near $x = 1$. To see this, we start by discussing the limit $x \rightarrow 0$ (i.e., $\theta \rightarrow \pi / 2$), which is known to be $+\infty$ by Proposition 6.

Table 1 Coefficients $\mathfrak {b} _n$ refereed to in Proposition 15

Proposition 14

Near $x = 0$, $\mu _n (x) = x ^{ -3/2 } (\mathfrak {a} _n + \mu _n ^L (x))$, $\mathfrak {a}_n > 0$, for some continuous functions $\mu _n ^L$ defined on $[0, \epsilon )$, $0< \epsilon < 1$, satisfying $\mu _n ^L (0) = 0$.

Proof

It suffices to show that $\lim _{ x \rightarrow 0 } x ^{ 3/2 } \mu _n (x) =\mathfrak {a}_n> 0$. Recall that

$$\begin{aligned} \sin ^2 d_{nk}=\sin ^2\theta (1-\cos k\phi ) [2-\sin ^2 \theta (1-\cos k\phi )]. \end{aligned}$$

As $\theta \rightarrow \pi / 2$, $\sin ^2d_{nk}, k\ne n$ remains positive except for $k=\frac{n}{2}$. Thus, all the terms in the two summations on the right-hand-side of (16) remain bounded as $\theta \rightarrow \pi /2$ (i.e., $x \rightarrow 0$), except for the one term corresponding to $k=\frac{n}{2}$. Then, if $n = 4l$, $l \in \mathbb {N}$, we have

$$\begin{aligned} \lim _{ x \rightarrow 0 } x ^{ 3/2 } \mu _n (x) =&\lim _{ \theta \rightarrow \pi /2} \frac{ -24\cos 2\theta \cos ^5\theta \sin ^2\theta }{\sin ^5 d_{n,n/2}}\\ =&\lim _{ \theta \rightarrow \pi /2} \frac{ -24\cos 2\theta \cos ^5\theta \sin ^2\theta }{ 32 \cos ^5\theta \sin ^5\theta }=\frac{3}{4}. \end{aligned}$$

Similarly, $n = 4l+2$, $l \in \mathbb {N}$, we have $\lim _{ x \rightarrow 0 } x ^{ 3/2 } \mu _n (x) =\frac{1}{4}.$ Thus, the claim follows. $\square$

Proposition 15

Near $x = 1$, $\mu _n (x) = (1-x) ^{ -3/2 } (\mathfrak {b} _n + \mu _n ^R (x))$, for some continuous function $\mu _n ^R$ defined on $(1-\epsilon , 1]$, $0< \epsilon < 1$, with $\mu _n ^R (0) = 0$. Moreover, $\mathfrak {b} _4 < 0$ and $\mathfrak {b} _n > 0$ for all $n > 4$, $n \in 2 \mathbb {N}$.

Fig. 2

Shown in (a) are the minimum values of $\mu _n (x)$. Sample plots of $\mu _n (x)$ shown in (b), (c) and (d)

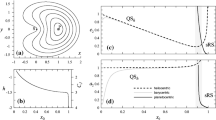
In lieu of a proof for Proposition 15, we offer the numerical evidence presented in Table 1, where we compute $\mathfrak {b} _n = \lim _{ x \rightarrow 1^{-} } (1-x) ^{ 3/2 } \mu _n (x)$ for $n = 4, 8, \ldots , 32$. Note that $\mathfrak {b} _4$ is the only negative number in the column.

It follows from Propositions 14 and 15, and the intermediate value theorem, that there is at least one root of $\mu _4 (x)$ on the interval (0, 1) . Using Mathematica’s numerical solver¹ (Wolfram Research, Inc. 2018), it is verified that there is exactly one root $x _4 ^*\in (0,1)$, $x _4 ^*\approx 0.70787$, (or $\theta \approx 0.571$, see Section 5.4). Thus, $\mu _4 (x) > 0$ for $x \in (0, x _4 ^*)$ and $\mu _4 (x) < 0$ for $x \in (x _4 ^*, 1)$. On the other hand,

Proposition 16

For $n > 4$, $n \in 2 \mathbb {N}$, $\mu _n (x)$ is strictly positive on the interval (0, 1) .

Again, in lieu of a proof, we offer the numerical evidence provided by Table 1. Using Mathematica’s numerical solver, we computed the critical points $x _n$ of $\mu _n (x)$ and verified that there is exactly one such critical point on the interval (0, 1) for each $n = 6, 8, \ldots , 32$. In the last column, we compute the corresponding critical values, all of them strictly positive. Propositions 14 and 15 then imply that such critical values are absolute minima on the interval (0, 1) . Note that these minima appear to be increasing as $n \rightarrow \infty$; the trend is shown in Fig. 2a for $n = 6, 8, \ldots , 64$. Figure 2b–d illustrate the graphs of $\mu _n (x)$ for $n = 4, 6, 12$.