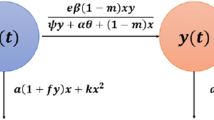Abstract
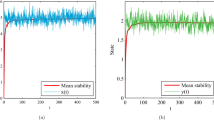
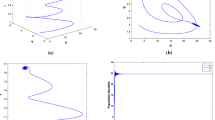
In this paper, we study a predator–prey reaction–diffusion model with seasonality and fear effect. In this model, the predator species reproduces only at a certain time of each year. We calculate the steady states of the system and study their stabilities, and then, we derive the conditions for Turing instability to occur. Numerical simulations show that (i) spatial patterns can emerge for Beddington–DeAngelis functional response, (ii) the system can have oscillatory behavior for both linear functional response and Beddington–DeAngelis functional response.



















Similar content being viewed by others
Availability of data and materials
The authors declare that the manuscript has no associated data.
References
Beddington, J.: Mutual interference between parasites or predators and its effect on searching efficiency. J. Anim. Ecol. 44, 331–340 (1975)
Casewell, H.: Matrix Population Models: Construction, Analysis and Interpretation. Sinauer Association, Sunderland, Masssachusetts (2001)
Creel, S., Christianson, D.: Relationships between direct predation and risk effects. Trends Ecol. Evol. 23(4), 194–201 (2008)
Cresswell, W.: Predation in bird populations. J. Ornithol. 152, 251–263 (2011)
DeAngelis, D., Goldstein, R., O’Neill, R.: A model for trophic interaction. Ecology 56, 881–892 (1975)
Fazly, M., Lewis, M., Wang, H.: On impulsive reaction-diffusion models in higher dimensions. SIAM J. Appl. Math. 77(1), 224–246 (2017)
Fazly, M., Lewis, M., Wang, H.: Analysis of propagation for impulsive reaction-diffusion models. SIAM J. Appl. Math. 80(1), 521–542 (2020)
Huang, Q., Wang, H., Lewis, M.: A hybrid continuous/discrete-time model for invasion dynamics of zebra mussels in rivers. SIAM J. Appl. Math. 77(3), 854–880 (2017)
Jiang, W., Cao, X., Wang, C.: Turing instability and pattern formations for reaction-diffusion systems on 2D bounded domain. Discrete Contin. Dyn. Syst. Ser. B 27(2), 1163–1178 (2022)
Kelley, W., Peterson, A.: Difference Equations: An Introduction with Applications, 2nd edn. Academic Press, San Diego (2001)
Kuznetsov, Y., Meijer, H.: Numerical Bifurcation Analysis of Maps: From Theory To Software. Cambridge University Press, Cambridge (2019)
Lewis, M., Li, B.: Spreading speed, traveling waves, and minimal domain size in impulsive reaction-diffusion models. Bull. Math. Biol. 74(10), 2383–2402 (2012)
Lima, S.: Nonlethal effects in the ecology of predator–prey interactions. Bioscience 48(1), 25–34 (1998)
Lima, S.: Predators and the breeding bird: behavioural and reproductive flexibility under the risk of predation. Biol. Rev. 84(3), 485–513 (2009)
Lin, Y., Wang, Q.: Spreading speed and traveling wave solutions in impulsive reactiondiffusion models. Commun. Nonlinear Sci. Numer. Simul. 23(1), 185–191 (2015)
Murray, J.: Mathematical biology II. Spatial Models and Biomedical Applications. Springer, New York (2001)
Ni, W., Tang, M.: Turing patterns in the Lengyel–Epstein system for the CIMA reaction. Trans. Am. Math. Soc. 357, 3953–3969 (2005)
Pachepsky, E., Nisbet, R., Murdoch, W.: Between discrete and continuous: consumer-resource dynamics with synchronized reproduction. Ecology 89, 280–288 (2008)
Peng, R., Yi, F., Zhao, X.: Spatiotemporal patterns in a reaction–diffusion model with the Degn–Harrison reaction scheme. J. Differ. Equ. 254, 2465–2498 (2013)
Shi, H., Ruan, S.: Spatial, temporal and spatiotemporal patterns of diffusive predator-prey models with mutual interference. IMA J. Appl. Math. 80, 1534–1568 (2015)
Singh, A., Nisbet, R.: Semi-discrete host-parasitoid models. J. Theor. Biol. 247(4), 733–742 (2007)
Turing, A.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B 237, 37–72 (1952)
Vasilyeva, O., Lutscher, F., Lewis, M.: Analysis of spread and persistence for stream insects with winged adult stages. J. Math. Biol. 72, 851–875 (2016)
Wang, X., Lutscher, F.: Turing patterns in a predator-prey model with seasonality. J. Math. Biol. 78, 711–737 (2019)
Wang, Z., Wang, H.: Persistence and propagation of a PDE and discrete-time map hybrid animal movement model with habitat shift driven by climate change. SIAM J. Appl. Math. 80(6), 2608–2630 (2020)
Wang, Z., Wang, H.: Bistable traveling waves in impulsive reaction-advection-diffusion models. J. Differ. Equ. 285, 17–39 (2021)
Wang, X., Zou, X.: Modeling the fear effect in predator-prey interactions with adaptive avoidance of predators. Bull. Math. Biol. 79, 1325–1359 (2017)
Wang, Y., Zou, X.: On a predator-prey system with digestion delay and anti-predation strategy. J. Nonlinear Sci. 30, 1579–1605 (2020)
Wang, J., Shi, J., Wei, J.: Dynamics and pattern formation in a diffusive predator-prey system with strong Allee effect in prey. J. Differ. Equ. 251, 1276–1304 (2011)
Wang, X., Zanette, L., Zou, X.: Modelling the fear effect in predator-prey interactions. J. Math. Biol. 73, 1179–1204 (2016)
Wang, Z., Salmaniw, Y., Wang, H.: Persistence and propagation of a discrete-time map and PDE hybrid model with strong Allee effct. Nonlinear Anal. Real World Appl. 61, 103336 (2021)
Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd edn. Springer-Verlag, New York (2003)
Wu, R., Zhao, X.: Spatial invasion of a birth pulse population with nonlocal dispersal. SIAM J. Appl. Math. 79(3), 1075–1097 (2019)
Yi, F., Wei, J., Shi, J.: Diffusion-driven instability and bifurcation in the Lengyel–Epstein system. Nonlinear Anal. Real World Appl. 9, 1038–1051 (2008)
Yi, F., Gaffney, E., Seirin-Lee, S.: The bifurcation analysis of Turing pattern formation induced by delay and diffusion in the Schnakenberg system. Discrete Contin. Dyn. Syst. Ser. B 22(2), 647–668 (2017)
Yi, F., Liu, S., Tuncer, N.: Spatiotemporal patterns of a reaction-diffusion substrate-inhibition Seelig model. J. Dyn. Differ. Equ. 29, 219–241 (2017)
Acknowledgements
The authors would like to thank Dr. Xiaoying Wang for sharing the numerical simulation data of paper (Wang and Lutscher 2019), which helped a lot in improving our numerical simulation codes. We thank the editors and the anonymous reviewers for their valuable comments, which helped to improve the presentation of this paper.
Funding
This research was supported by the National Natural Science Foundation of China (No. 12071491).
Author information
Authors and Affiliations
Contributions
TL contributed to writing—original draft. QW contributed to writing—review and editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interests.
Ethical Approval
Not applicable.
Additional information
Communicated by Anthony Bloch.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was supported by the National Natural Science Foundation of China (No. 12071491).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, T., Wang, Q. Turing Patterns in a Predator–Prey Reaction–Diffusion Model with Seasonality and Fear Effect. J Nonlinear Sci 33, 86 (2023). https://doi.org/10.1007/s00332-023-09938-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-023-09938-6
Keywords
- A predator–prey reaction–diffusion model
- Impulsive reproduction and fear effect
- Turing patterns
- Discrete systems