Abstract
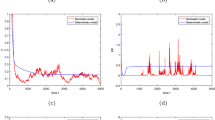
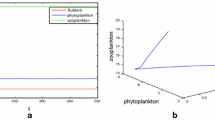
In this paper, we consider the stochastic nutrient–phytoplankton–zooplankton model with nutrient cycle. In order to take stochastic fluctuations into account, we add the stochastic increments to the variations of biomass of nutrition, phytoplankton and zooplankton during time interval \(\Delta t\), thus we obtain the corresponding stochastic model. Subsequently, we explore the existence, uniqueness and stochastically ultimate boundness of global positive solution. By constructing suitable Lyapunov function, we also obtain V-geometric ergodicity of this model. In addition, the sufficient conditions of exponential extinction and persistence in the mean of plankton are established. At last, we present some numerical simulations to validate theoretical results and analyze the impacts of some important parameters.
















Similar content being viewed by others
References
Arnold, L.: Stochastic differential equations: Theory and application (1972)
Arnold, E.M.: Aspects of a zooplankton, phytoplankton, phosphorus system. Ecol. Model. 5(4), 293–300 (1978)
Athreya, A., Kolba, T., Mattingly, J.: Propagating Lyapunov functions to prove noise-induced stabilization. Electron. J. Probab. 17, 1–38 (2012)
Bellet, L.R.: Ergodic properties of Markov processes. In: The Markovian Approach, Open Quantum Systems II, Springer (2006)
Cai, Y., Kang, Y., Wang, W.: A stochastic SIRS epidemic model with nonlinear incidence rate. Appl. Math. Comput. 305, 221–240 (2017)
Durrett, R.: Stochastic Calculus: A Practical Introduction, vol. 6. CRC Press (1996)
Hallam, T.G.: Structural sensitivity of grazing formulations in nutrient controlled plankton models. J. Math. Biol. 5(3), 269–280 (1978)
Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001)
Ikeda, N., Watanabe, S.: A comparison theorem for solutions of stochastic differential equations and its applications. Osaka J. Math. 14, 619–633 (1977)
Imhof, L., Walcher, S.: Exclusion and persistence in deterministic and stochastic chemostat models. J. Differ. Equ. 217(1), 26–53 (2005)
Jang, S.R.-J., Allen, E.J.: Deterministic and stochastic nutrient-phytoplankton-zooplankton models with periodic toxin producing phytoplankton. Appl. Math. Comput. 271, 52–67 (2015)
Ji, C., Jiang, D.: Threshold behaviour of a stochastic SIR model. Appl. Math. Model. 38(21–22), 5067–5079 (2014)
Mandal, P.S., Banerjee, M.: Deterministic and stochastic dynamics of a competitive phytoplankton model with allelopathy. Differ. Equ. Dyn. Syst. 21, 341–372 (2013)
Mao, X.: Stochastic Differential Equations and Applications. Elsevier (2007)
Mattingly, J.C., Stuart, A.M., Higham, D.J.: Ergodicity for SDEs and approximations: locally Lipschitz vector fields and degenerate noise. Stoch. Proc. Appl. 101(2), 185–232 (2002)
Riley, G.A., Stommel, H., Burrpus, D.P.: Qualitative ecology of the plankton of the western north atlantic. Bull. Bingham Oceanogr. Collect. 12, 1–169 (1949)
Ruan, S.: Persistence and coexistence in zooplankton-phytoplankton-nutrient models with instantaneous nutrient recycling. J. Math. Biol. 31, 633–654 (1993)
Rudnicki, R., Pichór, K., Tyran-Kamińska, M.: Markov semigroups and their applications. In: Dynamics of Dissipation, pp. 215–238. Springer (2002)
Smith, H.L., Waltman, P.: The Theory of the Chemostat: Dynamics of Microbial Competition, vol. 13. Cambridge University Press (1995)
Sun, S., Zhang, X.: Asymptotic behavior of a stochastic delayed chemostat model with nutrient storage. J. Biol. Syst. 26(02), 225–246 (2018)
Wang, L., Jiang, D.: Ergodic property of the chemostat: a stochastic model under regime switching and with general response function. Nonlinear Anal.-Hybri. 27, 341–352 (2018)
Wroblewski, J.S., Sarmiento, J.L., Flierl, G.R.: An ocean basin scale model of plankton dynamics in the north atlantic: 1. solutions for the climatological oceanographic conditions in may. Glob. Biogeochem. Cy. 2(3), 199–218 (1988)
Xu, C., Yuan, S.: Competition in the chemostat: a stochastic multi-species model and its asymptotic behavior. Math. Biosci. 280, 1–9 (2016)
Yu, X., Yuan, S., Zhang, T.: Asymptotic properties of stochastic nutrient-plankton food chain models with nutrient recycling. Nonlinear Anal-Hybri. 34, 209–225 (2019)
Zhang, X.: A stochastic non-autonomous chemostat model with mean-reverting Ornstein-Uhlenbeck process on the washout rate. J. Dyn. Differ. Equ. (2020). https://doi.org/10.1016/j.amc.2020.125833
Zhang, X., Yuan, R.: A stochastic chemostat model with mean-reverting Ornstein-Uhlenbeck process and Monod-Haldane response function. Appl. Math. Comput. 394, 125833 (2021)
Zhao, Q., Liu, S., Niu, X.: Stationary distribution and extinction of a stochastic nutrient-phytoplankton-zooplankton model with cell size. Math. Method. Appl. Sci. 43(7), 3886–3902 (2020)
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 12171039).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Kevin Painter.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, P., Zhang, X. & Yuan, R. Asymptotic Behavior of a Stochastic Generalized Nutrient–Phytoplankton–Zooplankton Model. J Nonlinear Sci 34, 94 (2024). https://doi.org/10.1007/s00332-024-10070-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-024-10070-2
Keywords
- Stochastic nutrient–phytoplankton–zooplankton model
- V-geometric ergodicity
- Exponential extinction
- Persistence in the mean
- Nutrient cycle