Abstract
The welfare state provides social insurance for lifetime risks. In that framework welfare stigma in form of a social norm against living off (net-)transfers is introduced, and the impact of welfare stigma on self-insurance and social insurance that works through redistributive taxation is analyzed. It turns out that introducing welfare stigma reduces the socially optimal self-insurance and raises the socially optimal social insurance. It may be efficient for the society to operate at a point on its opportunity frontier where an increase in risk taking decreases mean post-tax income and welfare stigma. In the presence of moral hazard self-insurance efforts are invariant with respect to welfare stigma whereas social insurance increases upon introducing welfare stigma. Furthermore, it is shown that self-insurance and social insurance are inefficiently low or high depending on the preference intensity of the social norm.

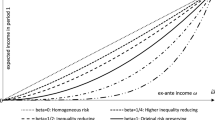
Efficient risk taking in dependence of the social norm









Similar content being viewed by others
Notes
Eichner and Wagener (2004) extend the analysis by welfare costs (administrative costs or shadow costs for public funds) and background risks. Within these extensions the efficient tax rate may be less than one.
Gong et al. (2009) analyze the case of group cooperation under uncertainty which is clearly related to social norms. However, we abstract from considering group settings.
The model at hand satisfies the location-scale condition of Meyer (1987) and Sinn (1973) and hence expected utility becomes a function of mean and variance. However, we do not assume that mean-variance preferences and expected utility need to be consistent and follow Ormiston and Schlee (2001) and Eichner (2008) and take the mean-variance framework as an approach that stands on its own.
The other case that welfare stigma increases in the share of net-transfer recipients is also analyzed.
It deserves to be mentioned that in Lindbeck et al. (1999) redistributive taxation is determined by majority voting.
We abstract from non-market income. Introducing non-market income would blow up the model without changing results and providing new insights.
Individuals are ex ante identical. After the veil of ignorance has lifted they differ with respect to income losses and incomes. Applying the law of large numbers the distribution of \(Y\) is then the ex post realized income distribution.
One might argue that living on welfare is a matter of luck in our setting and is therefore not subject to feelings of stigma. However, Lindbeck et al. (1999) considers productivity differences, reflected by a wage distribution, which constitute the share of transfer recipients in society. From an ex ante perspective, the revelation of this distribution could then also be interpreted as a matter of luck. Nevertheless, the question of how responsible and irresponsible factors shape stigma preferences is an interesting question but not subject to our analysis.
The specific functional form in (12) can be microfounded as follows. Suppose the individual is expected utility maximizer and let \(\breve{u}\) denote the von Neumann-Morgenstern utility function of income \(y\). The utility under certainty is given by
$$\begin{aligned} u(y) = \left\{ \begin{array}{lll} \breve{u}(y) &{} \text{ for } &{} \theta \le \hat{\theta },\\ \breve{u}(y) - a \breve{\Phi }(s) &{} \text{ for } &{} \theta > \hat{\theta }, \end{array}\right. \end{aligned}$$where \(\breve{\Phi }(s)\) represents welfare stigma. Then we obtain the expected utility
$$\begin{aligned} \mathbf E u(y) = (1-s) \mathbf E \breve{u}(y) + s \left[ \mathbf E \breve{u}(y)- a \breve{\Phi }(s) \right] = \mathbf E \breve{u}(y) - a s \breve{\Phi }(s). \end{aligned}$$The identities \(\mathbf E \breve{u}(y) \equiv U(\mu _Y, \sigma _Y)\) and \(\Phi (s) \equiv s \breve{\Phi }(s)\) establish (12).
Self-insurance affects \(\mathbf E \breve{u}(y) - a s \breve{\Phi }(s)\) from footnote 12 through \(s\) in two ways. It affects the ex-ante probability of getting a net-transfer reflected by the \(s\) before the stigma function \( \breve{\Phi }(s)\), and it changes the ex-post share of net-transfer recipients captured by \(s\) as argument of the stigma function \( \breve{\Phi }(s)\). In Sect. 2–5 we assume that the ex-post share effect overcompensates the ex-ante probability effect. This assumption goes back to the heart of the concept of welfare stigma (see Lindbeck et al. 1999 or Aronsson and Sjögren 2010). In view of expected utility in footnote 12 the ex-post share effect dominates, if and only if \(\Phi '(s)=\breve{\Phi }(s) +s \breve{\Phi }'(s)<0 \). The other case \(\Phi '(s) > 0\), where the ex-ante probability effect overompensates the ex-post stigma effect, is discussed in Sect. 6.
In our model expected utility and mean-standard deviation preferences are perfect substitutes. Since the interaction between individual’s choice (self-insurance or pre-tax standard deviation) and the source of uncertainty is linear, the model satisfies the location-scale property (Meyer 1987; Sinn 1983) such that all income distributions differ only by mean \(\mu _Y\) and standard deviation \(\sigma _Y\) of post-tax incomes.
More information about second-order conditions can be found in the Appendix.
Observe that each summand in the curly brackets is positive and that \(\frac{\partial \sigma ^*_X}{\partial a} > 0\).
This is line with the literature on welfare stigma. Lindbeck et al. (1999) employ a similar model structure. When individuals decide on working or not they treat the tax and transfer and therefore the share of transfer recipients in society as exogenously given. In a balanced-budget equilibrium a relationship between the tax and transfer system and the share of transfer recipients is established.
The derivation of (24) can be found in the Appendix 2.
It is worth mentioning that \(i_{\mu } =0\) is sufficient but not necessary for \( \frac{\partial \tilde{\sigma }_X}{\partial \tau }>0\).
Hence the economy is in a redistributive equilibrium.
The program for simulations is available from the authors upon request.
Given the highly stylized nature of our model the numerical example is not based on empirical data. Nevertheless, concerning the parameter \(c\) reflecting the operating costs we have chosen a value from the literature. OECD (2013) reports that administrative costs for tax administration as percentage of tax revenues range from 0.5 - 3 %. Evanc (2008) refers to different studies that estimate the compliance costs of income taxation between 2 % and 10 % of tax revenues. In the numerical example we have set the operating costs (as sum of administrative costs and compliance costs) \(c=0.075\) which amounts to 7.5 % and is in the middle of the range identified by Evanc (2008) and OECD (2013).
Observe that \(\tilde{\sigma }_X\) is independent of the norm parameter \(a\).
The sign of the indirect income effect is ambiguous.
In this case, the model could be extended by a different norm type similar to the work hours norm of Aronsson and Sjögren (2010) which focuses on the decisions at the intensive margin of labor supply.
The value \(\theta _{\mathrm {min}} = 0.3\) constitutes a lower boundary for the feasibility of the optimization problems. However, we can increase the minimum income loss to \(\theta _{\mathrm {min}} = 0.5\) without changing our results.
References
Andersen TM (2013) Incentive and insurance effects of income taxation. Bull Econ Res, in press
Andersen TM (2008) Unemployment insurance and taxation: incentives vs. insurance, discussion paper. Sept 2008
Aronsson T, Sjögren T (2010) Optimal income taxation and social norms in the labor market. Int Tax Public Financ 17(1):67–89
Besley T, Coate S (1992) Understanding welfare stigma: taxpayer resentment and statistical discrimination. J Public Econ 48(2):165–183
Bird EJ (2001) Does the welfare state induce risk-taking? J Public Econ 80:357–383
Clark AE (2003) Unemployment as a social norm: psychological evidence from panel data. J Labor Econ 21(2):323–351
Conlin M, Lynn M, O’Donoghue T (2003) The norm of restaurant tipping. J Econ Behav Org 52(3):297–321
Dufwenberg M, Lundholm M (2001) Social norms and moral hazard. Econ J 111(473):506–525
Eaton J, Rosen HS (1980a) Optimal redistributive taxation and uncertainty. Quart J Econ 95(2):357–364
Eaton J, Rosen HS (1980b) Taxation, human capital, and uncertainty. Am Econ Rev 70(4):705–715
Eaton J, Rosen HS (1980c) Labor supply, uncertainty and efficient taxation. J Public Econ 14(3):365–374
Ehrlich I, Becker GS (1972) Market insurance, self-insurance, and self-protection. J Polit Econ 80(4):623–648
Eichner T (2008) Mean variance vulnerability. Manag Sci 54(3):586–593
Eichner T, Wagener A (2004) The Welfare State in a Changing Environment. International Tax and Public Finance 11(3):313–331
Elster J (1989) Social norms and economic theory. J Econ Perspect 3(4):99–117
Evanc C (2008) Taxation compliance and administrative costs an overview. In: Lang M, Obermair C, Schuch J, Staringer C, Wenninger P (eds) Tax compliance costs in an enlarged European community. Vienna and Kluwer Law International, Linde Verlag, London, pp 447–468
Fehr E, Fischbacher U, Gächter S (2002) Strong reciprocity, human cooperation, and the enforcement of social norms. Human Nature 13(1):1–25
Gong M, Baron J, Kunreuther H (2009) Group cooperation under uncertainty. J Risk Uncertain 39(3):251–270
Homans GC (1974) Social behavior: its elementary form. Harcourt, Brace and World, New York
Lajeri-Chaherli F (2003) Partial derivatives, comparative risk behavior and concavity of utility functions. Math Soc Sci 46:81–99
Lajeri F, Nielsen LT (2000) Parametric characterizations of risk aversion. Econ Theory 15:469–475
Lindbeck A (1995) Hazardous welfare-state dynamics. Am Econ Rev 85(2):9–15
Lindbeck A, Nyberg S, Weibull JW (1999) Social norms and economic incentives in the welfare state. Q J Econ 114(1):1–35
Lindbeck A, Nyberg S, Weibull JW (2003) Social norms and welfare state dynamics. J Eur Econ Assoc 1(2–3):533–542
Lindbeck A, Nyberg S (2006) Raising children to work hard: altruism, work norms, and social insurance. Q J Econ 121(4):1473–1503
Linde J, Sonnemans J (2012) Social comparison and risky choices. J Risk Uncertain 44(1):45–72
Maccheroni F, Marinacci M, Rustichini A, Taboga M (2009) Portfolio selection with monotone mean-variance preferences. Math Financ 19(3):487–521
Markowitz H (1952) Portfolio selection. J Financ 7(1):77–91
Meltzer AH, Richard SF (1981) A rational theory of the size of government. J Polit Econ 89(5):914–927
Meyer J (1987) Two-moment decision models and expected utility maximization. Am Econ Rev 77(3):421–430
Mirrlees JA (1971) An exploration in the theory of optimum income taxation. Rev Econ Stud 38(2):175–208
Moffitt R (1983) An economic model of welfare stigma. Am Econ Rev 73(5):1023–1035
OECD (2013) Tax administration 2013: Comparative information on OECD and other advanced emerging economies. OECD Publishing
Ormiston MB, Schlee EE (2001) Mean-variance preferences and investor behaviour. Econ J 111(474):849–861
Rege M (2004) Social norms and private provision of public goods. J Public Econ Theory 6(1):65–77
Rege M, Telle K (2004) The impact of social approval and framing on cooperation in public good situations. J Public Econ 88(7):1625–1644
Roberts K (1977) Voting over income tax schedules. J Public Econ 8(3):329–340
Sherif M (1936) The psychology of social norms. Harper and Brothers, New York
Sinn H-W (1983) Economic decisions under uncertainty. North Holland, Amsterdam
Sinn H-W (1995) A theory of the welfare state. Scand J Econ 97(4):495–526
Sinn H-W (1996) Social insurance, incentives and risk taking. Int Tax Public Financ 3(3):259–280
Stutzer A, Lalive R (2004) The role of social work norms in job searching and subjective well-being. J Eur Econ Assoc 2(4):696–719
Traxler C (2010) Social norms and conditional cooperative taxpayers. Eur J Polit Econ 26(1):89–103
Varian HR (1980) Redistributive taxation as social insurance. J Public Econ 14(1):49–68
Wenzel M (2004) An analysis of norm processes in tax compliance. J Econ Psychol 25(2):213–228
Yamamura E (2008) Impact of formal and informal deterrents on driving behavior. J Socio-Econ 37(6):2505–2512
Yamamura E (2011) Effects of social norms and fractionalization on voting behaviour in Japan. Appl Econ 43(11):1385–1398
Author information
Authors and Affiliations
Corresponding author
Additional information
Helpful comments from two anonymous referees are gratefully acknowledged. Remaining errors are the authors’ sole responsibility.
Appendix
Appendix
1.1 Appendix 1: Derivation of (18) and (21)
Differentiation of the first-order condition for \(\sigma ^*_X\)
yields
The second equality in (34) follows from making use of the fist-order condition (33), (14) and \(i_{\mu } = - \frac{U_{\sigma \mu } U_{\mu } - U_{\sigma } U_{\mu \mu }}{U_{\mu }^2} = - \frac{1}{U_{\mu }} (U_{\sigma \mu } + i U_{\mu \mu })\). Observe that the first three summands in (34) are negative. Then a sufficient (but not necessary) condition for the second-oder condition being satisfied, formally \(A_{\sigma _X} < 0\), is \(U_{\mu \mu } <0\) (which displays risk aversion if expected utility approach and mean-variance approach are compatible) and
Note that \(F'\) is strictly positive while \(F''\) can be positive or negative. If \(F''<0\), then a sufficient condition for \(\frac{\partial ^2 s}{\partial \sigma ^2_X}<0\) might be \(F'' > - \frac{2 \sigma _X F'}{m c \sigma _{\theta }}\) as the bracket term in (37) must be positive. Then, (18) follows from \({\mathrm {sign}} \,\frac{\partial \sigma ^*_X}{\partial _a} = - {\mathrm {sign}} \,\frac{A_a}{A_{\sigma _X}} = {\mathrm {sign}} \,A_a\).
Next, differentiation of the first-order condition for \(\tau ^*\)
leads to
Observe that the second-order condition \(B_{\tau } + B_{\sigma _X} \frac{\partial \sigma ^*_X}{\partial \tau }<0\) is satisfied if \(\frac{\partial \sigma ^*_X}{\partial \tau } = -\frac{A_\tau }{A_{\sigma _X}} >0\). Under this presupposition
establishes (21).
1.2 Appendix 2: Derivation of (24)
Differentiating the first-order condition for \(\tilde{\sigma }_X\)
subject to \(\mu _Y = \bar{\mu } (\sigma _X) - c \tau (m-k \sigma _X)\) and \(\sigma _Y = (1-\tau ) \sigma _X\) we obtain
The comparative static effect (24) follows immediately from \(\frac{ \partial \tilde{\sigma }_X}{\partial \tau } = - \frac{C_\tau }{C_{\sigma _X}}\).
1.3 Appendix 3: Robustness check
In order to examine the robustness of the results in Sect. 5 we run further examples with different parameter values. We do so in Table 1 where we have changed the parameter \(c\) in row 1–6 all else equal as in the example of Sect. 5, \(\beta \) in row 7–12 all else equal as in the example of Sect. 5, and \(m\) in row 13–18 all else equal as in the example of Sect. 5. For each parameter constellation we have taken three different parameter values of \(a\). For a low value of \(a\), \(\tilde{\sigma }_X\) is inefficiently high and \(\tilde{\tau }\) is inefficiently low. For a middle value of \(a\), \(\tilde{\sigma }_X\) and \(\tilde{\tau }\) are approximately efficient, and for a high value of \(a\), \(\tilde{\sigma }_X\) is inefficiently low and \(\tilde{\tau }\) is inefficiently high. This does not only hold for \(c=0.01\) and \(c=0.13\) as shown in rows 1–6, but also for all \(c \in [0.01, 0.13]\). In addition, the Figs. 3, 4, 5, 6, 7, 8 9, and 10 remain qualitatively unchanged. For \(c \notin [0.01,0.03]\) we obtain corner solutions. Either one of the pre-tax standard deviations is negative or one of the tax rate is outside of the interval \([0, 1]\). Analogous arguments apply to variations in \(\beta \) and \(m\).Footnote 30
Rights and permissions
About this article
Cite this article
Eichner, T., Weinreich, D. Welfare stigma and risk taking in the welfare state. Soc Choice Welf 44, 319–348 (2015). https://doi.org/10.1007/s00355-014-0836-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-014-0836-5