A Hurwicz type result in a model with public good production

Abstract

A classic result in the theory of incentive compatibility is Hurwicz (Decision and organization: a volume in honor of Jacob Marschak, 1972). The paper showed that strategy-proof (SP), Pareto-efficient and individually rational social choice functions do not exist in two-good, two-agent exchange economies. This result has been extended in several ways, for instance, to arbitrary numbers of agents and goods and to restricted domains. In this paper, we extend the result to economies with production. We consider a two-good economy with a single public good that can be produced from a private good according to a convex cost function. Agents have initial endowments of the private good. We show that SP, Pareto-efficient, individually-rational and continuous social choice functions do not exist in this environment. Pareto-efficiency, individual rationality and continuity axioms apply only to a “small” domain of preferences parametrized by a real number.

Appendix

We provide a formal proof of Lemma 3.

Proof

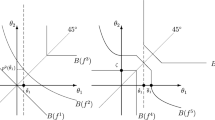
Let $(x_i^{\prime },y^{\prime }),(x_i^{\prime \prime },y^{\prime \prime })\in \mathfrak {R}_+^{2}$ and $\theta _i,\theta _i^{\prime }$ be specified in accordance with the statement of Lemma 3. Assume without loss of generality, $x_i^{\prime }<x_i^{\prime \prime }$ and $y^{\prime }>y^{\prime \prime }$. We note that $\theta _i<\theta _i^{\prime }$, in all the sections where Lemma 3 is used.

In Fig. 9, the points $(x_i^{\prime },y^{\prime })$ and $(x_i^{\prime \prime },y^{\prime \prime })$ are denoted by $a$ and $b$ respectively. Let $L(a,b)$ denote the line joining $a$ and $b$. The point of intersection of $L(a,b)$ and the $y$ axis is denoted by $c$. In view of our hypothesis, $IC(\theta _i,a)$ is not tangential to $L(a,b)$ at $a$, i.e it must intersect $L(a,b)$ at $a$.

Choose $\tilde{\theta }$ such that $\tilde{\theta }> \theta _i^{\prime }$. A direct computation of slopes at $a$ reveals that $IC(\tilde{\theta },a)$ cuts $IC(\theta _i,a)$ from above at $a$. Also, $IC(\tilde{\theta },b)$ cuts $IC(\theta _i^{\prime },b)$ from above at $b$.¹⁴

We denote the absolute value of the slope of $L(a,b)$ by $\bar{c}$. In view of our hypothesis, specifically condition (iv) we have,

$$\begin{aligned} \frac{\theta _i}{2\sqrt{x_i^{\prime \prime }}}> \bar{c} \implies \theta _i>2\bar{c}\sqrt{x_i^{\prime \prime }}. \end{aligned}$$

Thus we can choose $\hat{\theta }$ such that $\theta _i>\hat{\theta }>2\bar{c}\sqrt{x_i^{\prime \prime }}$. It follows from our construction that $IC(\hat{\theta },b)$ cuts $L(a,b)$ from above at $b$.

Fig. 9

Construction of a common concavified preference

The parameters $\tilde{\theta }$ and $\hat{\theta }$ chosen above can be used to construct a preference $R_i$ which is a concavification of $\theta _i$ at $(x_i^{\prime },y^{\prime })$ and $\theta _i^{\prime }$ at $(x_i^{\prime \prime },y^{\prime \prime })$. The regions $G_1$ and $G_2$ are indicated in Fig. 10. An additional parameter $t$ is computed as follows.

Fig. 10

Construction of a common concavified preference

Pick an arbitrary $(x_i,y)\in G_1$. Let $h= (x_i(h),y(h))$ be such that

• (i) $\tilde{\theta }\sqrt{x_i}+y=\tilde{\theta }\sqrt{x_i(h)}+y(h)$ and

• (ii) $[(x_i(h)<x_i^{\prime \prime }, y(h)>y^{\prime \prime })\ \text {and} (x_i(h),y(h))\ \text {lies on}\ L(c,b)]$ or $[x_i(h)\ge x_i^{\prime \prime }, y(h)=y^{\prime '}]$.

Let $t=\frac{x_i(h)}{x_i^{\prime }}$. The preference ordering $R_i$ is defined below.

$$\begin{aligned} R_i(x_i,y)= {\left\{ \begin{array}{ll} \tilde{\theta }\sqrt{x_i}+y-\sqrt{tx_i^{\prime }}(\tilde{\theta }-\hat{\theta }), &{} \text {if }\,(x_i,y)\in G_1 \\ \hat{\theta }\sqrt{x_i}+y, &{} \text {if }\,(x_i,y)\in G_2. \end{array}\right. } \end{aligned}$$

We omit the verification of the following facts.

• (i) $R_i$ is a classical preference.

• (ii) It concavifies $\theta _i$ at $(x_i^{\prime },y^{\prime })$ and $\theta _i^{\prime }$ at $(x_i^{\prime \prime },y^{\prime \prime })$.

Requirement (iv) in the statement of Lemma 3 ensures that the indifference curves for $R_i$ do not intersect each other. $\square$