Abstract
In this paper, we show that in pure exchange economies, any Pareto-efficient and strategy-proof allocation mechanism is alternately dictatorial; that is, it always allocates the total endowment to a single agent even if the receivers vary. While many studies have shown that such an allocation mechanism is dictatorial in two-agent economies, it has long remained an open question whether such a characterization can be obtained in many-agent economies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Following the seminal work of Hurwicz (1972), the manipulability and efficiency of allocation mechanisms in pure exchange economies have been studied intensively. In particular, Zhou (1991) established that any Pareto-efficient and strategy-proof allocation mechanism is dictatorial in exchange economies with two agents having classical (i.e., continuous, strictly monotonic, and strictly convex) preferences, and the dictatorship result in two-agent economies has been strengthened by being proved in restricted preference domains.Footnote 1
Compared with the result in two-agent economies, it has long been an open question whether such a characterization of Pareto-efficient and strategy-proof allocation mechanisms can be obtained in economies with many agents. From the perspective of assigning scare resources to the members of a society, it would be more natural to investigate the problem with many agents than just two agents.
In many-agent economies, there actually exist Pareto-efficient, strategy-proof, and non-dictatorial allocation mechanisms. Satterthwaite and Sonnenschein (1981) constructed such a mechanism, relying on the reverse dictator’s preference, to select one agent among the remaining agents, who is allocated the total endowment. Kato and Ohseto (2002) constructed a mechanism in economies with four or more agents, such that all agents have the opportunity to be allocated the total endowment. A specific feature shared by all known Pareto-efficient and strategy-proof allocation mechanisms is that a single agent receives all the goods even if the receivers vary. Such a mechanism is called alternately dictatorial. It has been conjectured but not proved that a Pareto-efficient and strategy-proof allocation mechanism is alternately dictatorial. This is what we prove in this paper.
Although the conjecture has remained an open question in its general form, some researchers have dealt with many-agent economies with additional conditions.
Some studies have shown the incompatibility of Pareto efficiency and strategy-proofness with allocation restrictions. Serizawa (2002) showed the incompatibility with the individual rationality restriction, where agents originally possess their initial endowments and a mechanism is assumed to allocate consumption that benefits all agents. Serizawa and Weymark (2003) showed the incompatibility with the minimum consumption guarantee restriction, where the consumption of each agent is assumed to be away from zero by some minimum distance. Momi (2013b) showed the incompatibility with a simple positivity restriction, where a mechanism is assumed to allocate positive consumption to all agents. On the contrary, Barberà and Jackson (1995) discarded Pareto efficiency and characterized strategy-proof mechanisms satisfying the individual rationality restriction. These allocation restrictions are so strong that they exclude any mechanism wherein some agents receive zero consumption. In particular, alternately dictatorial allocations violate these restrictions.
The non-bossiness condition has also been investigated. A mechanism is called non-bossy if a change in the preference of an agent does not affect the allocation as long as it does not affect the agent’s own consumption. Momi (2013b) showed that any Pareto-efficient, strategy-proof, and non-bossy mechanism is dictatorial. Goswami et al. (2014) showed that any Pareto-efficient, strategy-proof, non-bossy, and continuous mechanism is dictatorial even in the restricted domain of quasi-linear preferences. See Hatfield (2009) for a study of Pareto-efficient, strategy-proof, and non-bossy mechanisms in the context of allocating indivisible goods. The non-bossiness condition almost immediately implies that an alternately dictatorial mechanism is dictatorial; that is, it excludes a mechanism where the receivers of the total endowment vary.
Momi (2017) restricted the number of agents and proved that any Pareto-efficient and strategy-proof mechanism is alternately dictatorial when the number of agents is equal to or less than the number of goods. In this paper, we extend this approach to show the result without such a restriction on the numbers of agents and goods.
Here, we briefly explain the approach used in this paper. First, we recall the difference between economies with two agents and many agents. A crucial property of two-agent economies is the determinacy of allocation; that is, the consumption bundle assigned to one agent simultaneously determines the other agent’s consumption bundle because the sum of these consumption bundles equals the total endowment as long as the allocation is Pareto efficient. Then, we can change the preferences of agents and check the compatibility of the resulting allocations with strategy-proofness. To obtain the dictatorship result in a two-agent economy, starting from an allocation where both agents receive positive consumption, we can change the agents’ preferences and find two allocations that violate strategy-proofness.
Although such determinacy of allocation does not generally hold in many-agent economies, Momi (2017) focused on a situation in which the directions of the consumption of agents are linearly independent. A Pareto-efficient allocation uniquely determines the supporting price, and the supporting price vector uniquely determines the direction of possible consumption, which we call the consumption-direction vector, of each agent with a homothetic preference. If the consumption-direction vectors are independent among agents, there is a unique way to scale these vectors so that they sum to the total endowment. That is, under the independence of the consumption-direction vectors, the determinacy of allocation holds: the consumption bundle of an agent uniquely determines the other agents’ consumption bundles. This enables us to change agents’ preferences and check the compatibility of the resulting allocations with strategy-proofness. It is clear that the consumption-direction vectors cannot be independent in the commodity space when the number of agents exceeds the number of goods. For this reason, Momi (2017) needed to restrict the numbers of agents and goods.
How should we deal with many-agent economies without such a restriction? To obtain the alternate dictatorship result, we start from a non-alternately dictatorial allocation, under which at least two agents receive positive consumption and want to find allocations that violate strategy-proofness. As shown in Momi’s (2017) proof or as obviously observed in the case of two-agent economies, all we need is the determinacy of consumption among two agents, not the determinacy of all agents’ consumption.
Thus, we focus on the situation in which two agents, who receive positive consumption, have different consumption-direction vectors and all the other agents have the same consumption-direction vector that is different from those of the two agents. For example, let agents 1 and 2 receive positive consumption. We focus on the situation in which agents 1, 2, and 3 have different consumption-direction vectors and the consumption-direction vector of any other agent equals that of agent 3. The determinacy of consumption holds among agents 1 and 2. The consumption bundle of agent 1 uniquely determines agent 2’s consumption bundle and the sum of the other agents’ consumption bundles because agent 2’s and agent 3’s consumption-direction vectors should be uniquely scaled up so that they sum to the total endowments minus agent 1’s consumption bundle. In the same manner, agent 2’s consumption bundle determines agent 1’s uniquely.
Now, our problem is how we can reach the situation explained above, starting from a preference profile where the allocation is not dictatorial. If two agents have the same preference, then they always have the same consumption-direction vectors. However, it seems impossible to replace the preferences of all agents except two agents with the same preference. In this paper, we consider preferences that are partially identical. We say that two preferences are partially identical when their indifference sets coincide in a subset of the commodity space. We replace all agents’ preferences with preferences that are partially identical and change the preferences of two agents who receive positive consumption so that the other agents’ consumption-direction vectors coincide in the identical part of the preferences, and the three consumption-direction vectors, namely those of the two agents and the other agents, are different. In Sect. 3, we explain more in detail why we cannot replace agents’ preferences with the same preference and how we replace them with partially identical preferences.
The rest of the paper is organized as follows. Section 2 describes the model and results. Section 3 defines partially identical preferences and explains why we need them. Section 4 reveals that the option set in our setup is the smooth surface of a strictly convex set, as Momi (2017) proved under the independence of the consumption-direction vectors. Sections 5 and 6 provide the proofs of the results in Sect. 2. Section 7 contains concluding remarks. The Appendix contains the proofs for the properties of the option set given in Sect. 4.
2 Model and results
We consider an economy with N agents, indexed by \(i=1,\ldots , N\), where \(N\ge 2\), and L goods, indexed by \(l=1,\ldots , L\), where \(L\ge 2\). The consumption set for each agent is \(R_{+}^L\). A consumption bundle for agent i is a vector \(x^i=(x_1^i,\ldots ,x_L^i)\in R_+^L\). The total endowment of goods for the economy is \(\Omega =(\Omega _1,\ldots ,\Omega _L)\in R_{++}^L\). An allocation is a vector \(\mathbf{x }=(x^1,\ldots ,x^N)\in R_{+}^{LN}\). Thus, the set of feasible allocations for the economy with N agents and L goods is
A preference R is a complete, reflexive, and transitive binary relation on \(R_{+}^L\). The corresponding strict preference \(P_R\) and indifference \(I_R\) are defined in the usual way. For any x and \(x'\) in \(R_+^L\), \(xP_R x'\) implies that \(xRx'\) and not \(x'Rx\), and \(xI_Rx'\) implies that \(xRx'\) and \(x'Rx\). Given a preference R and a consumption bundle \(x\in R_+^L\), the upper contour set of R at x is \(UC(x; R)=\{x'\in R_+^L:x'Rx\}\) and the lower contour set of R at x is \(LC(x; R)=\{x'\in R_+^L:xRx'\}\). We let \(I(x;R)=\{x'\in R_+^L:x'I_Rx\}\) denote the indifference set of R at x, and \(P(x; R)=\{x'\in R_+^L:x'P_Rx\}\) denotes the strictly preferred set of R at x.
A preference R is continuous if UC(x; R) and LC(x; R) are both closed for any \(x\in R_+^L\). A preference R is strictly convex on \(R_{++}^L\) if UC(x; R) is a strictly convex set in \(R^L\) for any \(x\in R_{++}^L\). A preference R is monotonic if for any x and \(x'\) in \(R_{+}^L\), \(x>x'\) implies that \(xRx'\).Footnote 2 A preference R is strictly monotonic on \(R_{++}^L\) if for any x and \(x'\) in \(R_{++}^L\), \(x>x'\) implies that \(xP_Rx'\).Footnote 3 A preference R is homothetic if for any x and \(x'\) in \(R_+^L\) and any \(t>0\), \(xRx'\) implies that \((tx)R(tx')\). A preference R is smooth if for any \(x\in R_{++}^L\), there exists a unique vector \(p\in S_{+}^{L-1}\equiv \{x\in R_{+}^L:\parallel x\parallel =1\}\) such that p is the normal of a supporting hyperplane to UC(x; R) at x, where \(\parallel \cdot \parallel\) denotes the Euclid norm in \(R^L\). We call the vector p the gradient vector of R at x, and write \(p=p(R,x)\). If R is smooth, strictly convex on \(R_{++}^L\), and strictly monotonic on \(R_{++}^L\), then the gradient vector is positive in the positive orthant: \(p(R,x)\in S_{++}^{L-1}\equiv \{x\in R_{++}^L:\parallel x\parallel =1\}\) for any \(x\in R^L_{++}\).
We call a preference classical when it is continuous, strictly convex on \(R_{++}^L\), and strictly monotonic on \(R_{++}^L\), and let \({\mathcal{R}}_C\) denote the set of classical preferences. Furthermore, we let \({\mathcal{R}}\) denote the set of classical, smooth, and homothetic preferences. In this paper, we prove the main result in the restricted domain \({\mathcal{R}}\) and extend it to \({\mathcal{R}}_C\) as a corollary.
A preference profile is an N-tuple \(\mathbf{R } =(R^1,\ldots ,R^N)\in{{\mathcal{R}}}^N\). We write the subprofile obtained by removing \(R^i\) from \(\mathbf{R }\) as \(\mathbf{R }^{-i}=(R^1,\ldots ,R^{i-1},R^{i+1},\ldots ,R^N)\) and write the profile \((R^1,\ldots ,R^{i-1},\bar{R}^i,R^{i+1},\ldots , R^N)\) as \((\bar{R}^i,\mathbf{R }^{-i})\). We also write \(\mathbf{R }^{-\{i,j\}}\) to denote the subprofile obtained by removing \(R^i\) and \(R^j\) from \(\mathbf{R }\).
A social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) assigns a feasible allocation to each preference profile in \({{\mathcal{R}}}^N\). For a preference profile \(\mathbf{R }\in{{\mathcal{R}}}^N\), the outcome chosen can be written as \(f(\mathbf{R })=(f^1(\mathbf{R }),\ldots ,f^N(\mathbf{R }))\), where \(f^i(\mathbf{R })\) is the consumption bundle allocated to agent i by f. The efficiency, strategy-proofness, and dictatorship of f is defined as follows.
Definition 1
A social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is strategy-proof if \(f^i(\mathbf{R }) R^if^i(\bar{R}^i,\mathbf{R }^{-i})\) for any \(i=1,\ldots , N\), any \(\mathbf{R }\in{{\mathcal{R}}}^N\), and any \(\bar{R}^i\in{{\mathcal{R}}}\).
A feasible allocation is Pareto efficient if no other feasible allocation would benefit someone without making anyone else worse off. That is, \(\mathbf{x }\in X\) is Pareto efficient for the preference profile \(\mathbf{R }\) if there exists no \(\bar{\mathbf{x }}\in X\) such that \(\bar{x}^iR^ix^i\) for any agent \(i=1,\ldots , N\) and \(\bar{x}^jP_{R^j}x^j\) for some agent \(j\in \{1,\ldots ,N\}\). A social choice function is Pareto efficient if it always assigns a Pareto-efficient allocation.
Definition 2
A social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is Pareto efficient if \(f(\mathbf{R })\) is Pareto efficient for any \(\mathbf{R }\in{{\mathcal{R}}}^N\).
A social choice function is dictatorial if there exists an agent who is always allocated the total endowment.
Definition 3
A social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is dictatorial if there exists \(i\in \{1,\ldots , N\}\) such that \(f^i(\mathbf{R })=\Omega\) for any \(\mathbf{R }\in{{\mathcal{R}}}^N\).
We say that a social choice function is alternately dictatorial if it always allocates the total endowment to some single agent. Under an alternately dictatorial social choice function, the identity of the receiver of the total endowment may vary depending on the preference profiles.
Definition 4
A social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is alternately dictatorial if for any \(\mathbf{R }\in{{\mathcal{R}}}^N\), there exists \(i_\mathbf{R }\in \{1,\ldots ,N\}\) such that \(f^{i_\mathbf{R }}(\mathbf{R })=\Omega\).
This paper’s main result is as follows.
Theorem
Any Pareto-efficient and strategy-proof social choice function\(f:{{\mathcal{R}}}^N\rightarrow X\)is alternately dictatorial.
This is proved in the preference domain \({\mathcal{R}}\). Let \(\bar{{\mathcal{R}}}\) be a preference domain such that \({\mathcal{R}}\subset \bar{{\mathcal{R}}}\subset{{\mathcal{R}}}_C\), and let us extend Definitions 1–4 to \(\bar{{\mathcal{R}}}\).
Corollary
Any Pareto-efficient and strategy-proof social choice function\(f:\bar{{\mathcal{R}}}^N\rightarrow X\)is alternately dictatorial.
Before we end this section, we explain some additional setups we need. We say that a social choice function is pseudo-efficient if it allocates a Pareto-efficient allocation or allocates zero consumption to all agents.
Definition 5
A social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is pseudo-efficient if for any \(\mathbf{R }\in{{\mathcal{R}}}^N\), \(f(\mathbf{R })\) is Pareto efficient or \(f^i(\mathbf{R })=0\) for any \(i=1,\ldots ,N\).
If a social choice function is Pareto efficient, then it is also pseudo-efficient. Until the proof of the corollary provided in Sect. 6, we prove all the results with a pseudo-efficient social choice function rather than with a Pareto-efficient social choice function. This is because, in the proof of the corollary, we apply the results to a subeconomy with \(N'(<N)\) agents and we should consider the case in which all agents in the subeconomy receive zero consumption. Pseudo-efficiency in such a subeconomy does not contradict Pareto efficiency in the whole economy.
We often consider a social choice function f that satisfies efficiency and strategy-proofness only on a subset \({\mathcal{A}}=\Pi _{i=1}^N{\mathcal{A}}^i\subset{{\mathcal{R}}}^N\), where \({\mathcal{A}}^i\subset{{\mathcal{R}}}\). We say that a social choice function f is strategy-proof on \({\mathcal{A}}\) if \(f^i(\mathbf{R }) R^if^i(\bar{R}^i,\mathbf{R }^{-i})\) for any \(i=1,\ldots , N\), any \(\mathbf{R }\in{\mathcal{A}}\), and any \(\bar{R}^i\in{\mathcal{A}}^i\). We say a social choice function f is Pareto efficient on \({\mathcal{A}}\) if \(f(\mathbf{R })\) is Pareto efficient for any \(\mathbf{R }\in{\mathcal{A}}\). We say a social choice function f is pseudo-efficient on \({\mathcal{A}}\) if for any \(\mathbf{R }\in{\mathcal{A}}\), \(f(\mathbf{R })\) is Pareto efficient or \(f^i(\mathbf{R })=0\) for any \(i=1,\ldots ,N\).
We let A denote the feasible consumption set for an agent:
It is straightforward to observe that if \(f(\mathbf{R })\) is a Pareto-efficient allocation, then \(f^i(\mathbf{R })\) is not on the boundary of A except zero and \(\Omega\); that is, \(f^i(\mathbf{R })\in int A\bigcup \{0,\Omega \}\), where intA denotes the interior of A. See Momi (2017) for the formal proof. To establish the alternate dictatorship result, we assume \(f^i(\mathbf{R })\in int A\) at a preference profile \(\mathbf{R }\) and show a contradiction.
As in previous studies including Serizawa (2002) and Momi (2017), we discuss the continuity in \({\mathcal{R}}\) with respect to the Kannai metric. For \(x\in R_+^L\setminus \{0\}\), [x] denotes the ray starting from zero and passing through x: \([x]=\{y\in R^L_+:y=tx, t\ge 0\}\). We define \(\mathbf{1 }\equiv (1,\ldots ,1)\in R_+^L\) so that \([\mathbf{1 }]\) denotes the principal diagonal of \(R_+^L\). Using these definitions, the Kannai metric \(d(R,R')\) for continuous and monotonic preferences R and \(R'\) is defined as
With the Kannai metric, \({\mathcal{R}}\) is a metric space. See Kannai (1970) for the details. In this paper, we write \({\mathcal{B}}_\epsilon (\bar{R})\subset{{\mathcal{R}}}\) to denote the open ball set of preferences in \({{\mathcal{R}}}\) with center \(\bar{R}\) and radius \(\epsilon\): \({\mathcal{B}}_\epsilon (\bar{R}) =\{R\in{{\mathcal{R}}}:d(R,\bar{R})<\epsilon \}\).
For a preference \(R\in{{\mathcal{R}}}\) and a consumption bundle \(x\in R_+^L\), a preference \(\bar{R}\) is called a Maskin monotonic transformation (MMT, hereafter) of R at x if \(\bar{x}\in UC(x; \bar{R})\) and \(\bar{x}\ne x\) implies that \(\bar{x}P_Rx\). It is well known that if an agent receives x at a preference profile \(\mathbf{R }\), strategy-proofness implies that this agent receives the same consumption bundle x when the agent’s preference is subject to an MMT at x. As shown by Momi (2013b, Lemma 4), for a preference \(R\in{{\mathcal{R}}}\) and a consumption bundle \(x\in R_{++}^L\), there exists a preference that is an MMT of R at x in any neighborhood of R.
For any subset \(B\subset R^L\) we let \(\overline{B}\) denote the closure of B and \(\partial B\) denote the boundary of B. For any subsets B and C in \(R^L\), we write \(B+C=\{b+c\in R^L: b\in B, c\in C\}\) and \(B-C=\{b-c\in R^L: b\in B, c\in C\}\). For a price vector \(p\in S^{L-1}_{++}\) and a consumption vector \(y\in R^{L}_+\), \(p^\perp =\{x\in R^L:px=0\}\) denotes the hyperplane perpendicular to p passing through the origin and \(y+p^\perp\) denotes the hyperplane perpendicular to p passing through y. In this paper, we write \(D_\epsilon (\bar{x})\subset R^L\) to denote the open ball in \(R^L\) with center \(\bar{x}\) and radius \(\epsilon\): \(D_\epsilon (\bar{x})=\{x\in R^L:\parallel x-\bar{x} \parallel <\epsilon \}\) and write \(\bar{D}_\epsilon (\bar{x})\subset R^L\) to denote the closed ball with center \(\bar{x}\) and radius \(\epsilon\): \(\bar{D}_\epsilon (\bar{x})=\{x\in R^L:\parallel x-\bar{x}\parallel \le \epsilon \}\).
3 Partially identical preferences
If a social choice function f is Pareto efficient, all agents share the same gradient vector at their consumption \(f^i(\mathbf{R })\) as long as the consumption is positive and the gradient vector is well defined. We call this vector the price vector at the allocation \(f(\mathbf{R })\) and write \(p(\mathbf{R }, f)\in S_{++}^{L-1}\).
On the contrary, for a preference \(R\in{{\mathcal{R}}}\) and a price vector \(p\in S_{++}^{L-1}\), we let \(g(R,p)\in S_{++}^{L-1}\) denote the normalized consumption vector where the gradient vector of R is p. The normalized consumption vector is a continuous function of p because a preference R is smooth and strictly convex in \(R_{++}^L\).
As mentioned above, the price vector depends on the social choice function: \(p=p(\mathbf{R }, f)\). We call \(g^i(\mathbf{R },f)\equiv g(R^i,p(\mathbf{R },f))\) agent i’s consumption-direction vector at the preference profile \(\mathbf{R }\) under f because the agent’s consumption \(f^i(\mathbf{R })\) should be on the ray \([g^i(\mathbf{R },f)]\). Note that the consumption-direction vector \(g^i(\mathbf{R },f)\) is defined even if the agent is given zero consumption \(f^i(\mathbf{R })=0\). We can write \(f^i(\mathbf{R })=\parallel f^i(\mathbf{R })\parallel g^i(\mathbf{R },f)\).
Under the assumption of \(N\le L\), Momi (2017) focused on a preference profile \(\bar{\mathbf{R }}\) where the consumption-direction vectors are independent. The role of this independence should be clear. Consumption vectors \(f^i(\bar{\mathbf{R }})\), \(i=1,\ldots ,N\), are on the rays \([g^i(\bar{\mathbf{R }},f)]\), \(i=1,\ldots ,N\), respectively, and they sum to the total endowment \(\Omega\). Therefore, an agent’s positive consumption \(f^i(\bar{\mathbf{R }})\) determines the price vector as the agent’s gradient vector \(p(\bar{\mathbf{R }},f)=p(\bar{R}^i, f^i(\bar{\mathbf{R }}))\), and the price vector determines all agents’ consumption-direction vectors \(g^i(\bar{\mathbf{R }},f)\), and then all agents’ consumption bundles are determined uniquely to sum to the total endowment \(\Omega\). That is, the determinacy of consumption holds among all agents: an agent’s consumption bundle determines other agents’ consumption bundles. Thus, Momi (2017) showed that if two agents receive positive consumption, then an agent’s preference changes determine not only the changes of the agent’s consumption bundle but also the other agent’s, which could induce allocations contradicting the strategy-proofness of f.
It is clear that the consumption-direction vectors of N agents cannot be independent in \(R^L\) when there are many agents \(N>L\). In this paper, we focus on a preference profile where all agents except two have the same consumption-direction vectors. Without loss of generality, we assume agents \(i\ge 3\) are such agents. Let \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\) be a preference profile such that \(g^i(\bar{\mathbf{R }}, f)=g^3(\bar{\mathbf{R }}, f)\) for \(i\ge 3\). We suppose that the three consumption-direction vectors \(g^i(\bar{\mathbf{R }}, f)\)\(i=1,2,3\), are all different: \(g^i(\bar{\mathbf{R }},f)\ne g^j(\bar{\mathbf{R }},f)\) for any \(i,j\in \{1,2,3\}\) such that \(i\ne j\). Agents 1 and 2’s consumption bundles are on the rays \([g^1(\bar{\mathbf{R }}, f)]\) and \([g^2(\bar{\mathbf{R }}, f)]\), respectively and the sum of the other agents’ consumption bundles is on the ray \([g^3(\bar{\mathbf{R }}, f)]\). That is, the determinacy of consumption holds among agents 1 and 2: agent 1’s (resp. 2’s) consumption bundle determines agent 2’s (resp. 1’s) consumption bundle. Thus, if agents 1 and 2 receive positive consumption, then an agent’s preference changes determine the changes of the other agent’s consumption, which would induce allocations contradicting the strategy-proofness of f.
How can we reach such a preference profile where the determinacy of consumption among two agents holds, starting from a preference profile \(( R^1,\ldots , R^N)\) where two agents are given positive consumption? This can be easily achieved if an agent, say agent 1, is ensured to always have positive consumption different from the total endowment. Then, we simply replace each of the other agents’ preferences \(\bar{R}^i\), \(i\ne 1\), with a preference \(R^{*}\). Then, at the preference profile \((\bar{R}^1,R^{*},\ldots , R^{*})\), agent 1 still has positive consumption different from the total endowment because of the assumption. Since there exists another agent, say agent 2, who receives positive consumption at the preference profile \(( R^1,R^{*},\ldots , R^{*})\), we replace the agent’s preference \(R^{*}\) with a slightly different preference \(\hat{R}^2\) so that its consumption-direction vector differs from those for \(R^{*}\) and \(R^1\). Then, at the preference profile \((R^1, \hat{R}^2, R^{*}, \ldots ,R^{*})\), agents 1 and 2 have positive consumption and the other agents \(i\ge 3\) have the same consumption-direction vector as we desired.
Without such an assumption of positive consumption, we immediately face difficulties. First, we cannot replace an agent’s preference \(R^i\) with \(R^{*}\) when the agent’s consumption is zero. When we replace the preference of an agent receiving zero consumption, any resulting allocation is compatible with strategy-proofness as long as the agent’s resulting consumption is still zero. In particular, if one of the other agents receives the total endowment as a result of the replacement, such an allocation is compatible with Pareto efficiency and strategy-proofness, and hence we cannot proceed any more toward the aforementioned preference profile that would induce a contradiction. Therefore, we can only replace the preference of an agent receiving positive consumption. Can we repeat such replacements until we reach the desired preference profile? Such an attempt would fail, as described next. Suppose we have completed the replacement of the preferences of K agents, say agents \(3,\ldots , K+2\)’s, with \(R^{*}\)’s, agents 1 and 2 have positive consumption at the preference profile \(( R^1, R^2, R^{*},\ldots ,R^{*}, R^{K+3},\ldots , R^N)\), and the consumption-direction vectors of agents 1, 2, and 3 are different. The non-existence of an agent \(i\ge K+3\) receiving positive consumption induces a contradiction in the economy that consists of agents \(1,\ldots ,K+2\), where all agents but agents 1 and 2 have the same gradient vector, and hence the determinacy of consumption holds among agents 1 and 2. Therefore, there exists another agent, say agent \(K+3\), who receives positive consumption. One problem is that the replacement of agent \(K+3\)’s preference \(R^{K+3}\) with \(R^{*}\) might cause either agent 1 or agent 2 to receive zero consumption. For example, let agent 2 receive zero consumption. Then, we have to replace the preference of an agent among agents \(3,\ldots , K+3\) who have positive consumption so that its consumption-direction vector is different from that for \(R^{*}\) to ensure the determinacy of consumption among agent 1 and this agent. For example, we replace agent \(K+3\)’s preference \(R^{*}\) with \(\hat{R}^{K+3}\) so that its consumption-direction vector is slightly different from that for \(R^{*}\). As a result, at the preference profile \(( R^1, R^2, R^{*},\ldots ,R^{*}, \hat{R}^{K+3}, R^{N+4},\ldots , R^N)\), agents 1 and \(K+3\) have positive consumption and the consumption-direction vectors for \(R^1\), \(\hat{R}^{K+3}\), \(R^{*}\) are different. However, the number of agents who have the preference \(R^{*}\) is still K. We cannot increase the number of such agents.
To overcome this difficulty, we replace all agents’ preferences including those of agents 1 and 2 in the above discussion with preferences \(\tilde{R}^1,\ldots ,\tilde{R}^N\) that are “partially” identical. We say preferences are partially identical when their indifference sets coincide in a subset of the commodity space. Then, their consumption-direction vectors are the same as long as the vectors are in the subset in which the indifference sets coincide.
Parallel to the above discussion, suppose that we have completed the replacement of agents \(1,\ldots ,K+2\)’s preferences with partially identical preferences and agents 1, 2, and \(K+3\) receive positive consumption at the preference profile \((\tilde{R}^1,\ldots , \tilde{R}^{K+2}, R^{K+3},\ldots , R^{N})\). Suppose the replacement of agent \(K+3\)’s preference \(R^{K+3}\) with \(\tilde{R}^{K+3}\) causes agent 2 to receive zero consumption. We assume the consumption-direction vectors for agents \(2,\ldots K+3\) are the same because they are in the identical part of the preferences by slightly changing agent 1’s preference if needed. We replace the preference of an agent among agents \(3,\ldots , K+3\) who have positive consumption so that the agent’s consumption-direction vector differs from the others’. For example, we replace agent \(K+3\)’s preference \(\tilde{R}^{K+3}\) with \(\hat{R}^{K+3}\) so that the agent’s consumption-direction vector is slightly different from the others’ and agents \(2,\ldots ,K+2\)’s consumption-direction vector is the same. As a result, at the preference profile \((\tilde{R}^1,\ldots ,\tilde{R}^{K+2},\hat{R}^{K+3}, R^{N+4},\ldots , R^N)\), agents 1 and \(K+3\) have positive consumption, agents \(2,\ldots , K+2\) have the same consumption-direction vector even if agent 2 has zero consumption, and this consumption-direction vector, agent 1’s and \(K+3\)’s are different as desired. Note that the number of agents who have the same consumption-direction vector is \(K+1\). Furthermore, we can take the preference \(\hat{R}^{K+3}\) close to \(\tilde{R}^{K+3}\) so that \(\tilde{R}^1,\ldots ,\tilde{R}^{K+2}\) and \(\hat{R}^{K+3}\) are still identical in a probably smaller subset of the commodity space. By repeating this argument, we reach the preference profile where two agents receive positive consumption and the other agents have the same consumption-direction vector, which is in the identical part of their preferences. This intuitive explanation is formally stated in Proposition 3.
Formally, we define the partial identity of preferences as follows. We say that preferences R and \(R'\) are identical in a set \(B\subset R_{+}^L\) if their indifference sets coincide in B.
Definition 6
For any set \(B\subset R_{+}^L\), preferences R and \(R'\) in \({{\mathcal{R}}}\) are identical in B when \(I(x;R)\bigcap B=I(x;R')\bigcap B\) for any \(x\in B\).
In this paper, we consider preferences that are identical in or outside a cone. For an open convex set C in the simplex \(\{x\in R_{+}^L:\sum _{l=1}^Lx_l=1\}\), we call the union of rays passing through \(x\in C\), \(\bigcup _{x\in C}[x]\), a cone. We let \({\mathcal{Q}}\) denote the set of such cones. For a preference \(R\in{{\mathcal{R}}}\) and a cone \(Q\in{\mathcal{Q}}\), we define \({{\mathcal{R}}}(R, Q)\) as the set of preferences identical to R in Q and \({{\mathcal{R}}}(R, Q^c)\) as the set of preferences identical to R in \(Q^c\equiv R_{+}^L\setminus Q\); that is, identical to R outside Q. As we deal with homothetic preferences, if \(I(x;R)\bigcap Q=I(x;R')\bigcap Q\) for a vector x in a cone Q, then R and \(R'\) are identical in Q.
Fix a preference \(\bar{R}\), a cone Q, and a smaller cone \(Q'\) strictly included in Q: \(\overline{Q'}\setminus \{0\}\subset Q\). When a preference R is sufficiently close to \(\bar{R}\), it would not be difficult to imagine a preference that is identical to \(\bar{R}\) outside Q and identical to R in \(Q'\).
Lemma 1
Consider two preferences\(\bar{R}\)andRin\({{\mathcal{R}}}\)and two cones\(Q'\)andQin\({\mathcal{Q}}\)such that\(\overline{Q'}\setminus \{0\}\subset Q\). If\(\bar{R}\)andRare sufficiently close, then there exists a preference\(\hat{R}\in{{\mathcal{R}}}\)that is identical toRin\(Q'\)and identical to\(\bar{R}\)in\(Q^c\).
See Appendix for the proof of Lemma 1.
Suppose a preference \(\bar{R}\in{{\mathcal{R}}}\), a consumption vector \(x\in R_{++}^L\), and a cone \(Q\in{\mathcal{Q}}\) such that \(x\in Q\) are given. For a preference R sufficiently close to \(\bar{R}\), we often consider a preference \(\hat{R}\) that is identical to R in a neighborhood of x and identical to \(\bar{R}\) outside Q. That is, \(\hat{R}\in{{\mathcal{R}}}(\bar{R},Q^c)\) and the binary relation of \(\hat{R}\) is given by R in a neighborhood of x. The existence of such a preference \(\hat{R}\) is clear from Lemma 1 because there exists a cone \(Q'\) such that \(x\in Q'\) and \(\overline{Q'}\setminus \{0\}\subset Q\).
4 Option set
In this section, we review the option set and its topological properties. For agent i, when the other agents’ preferences \(\bar{\mathbf{R }}^{-i}\) are fixed, the option set is generally defined as the union of the agent’s consumption bundles given by f over his preferences \(R^i\) in \({{\mathcal{R}}}\):
If f is strategy-proof, \(f^i(R^i,\bar{\mathbf{R }}^{-i})\) should be the most preferred consumption bundle in the option set with respect to \(R^i\). Thus the option set tells us how the consumption given by f changes when the agent’s preferences change.
If a social choice function is alternately dictatorial, then the option set is a single element set \(\{0\}\) or \(\{\Omega \}\). To prove the alternate dictatorship result, we assume \(f^i(\mathbf{R })\in intA\) and study the option set in a neighborhood of the consumption \(f^i(\mathbf{R })\) to induce a contradiction. We also study the option set under the assumption that the social choice function is efficient and strategy-proof on a subset of the preference set \({{\mathcal{R}}}^N\).
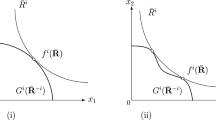
Momi (2017) proved that if a social choice function f is pseudo-efficient and strategy-proof in a neighborhood of a preference profile \(\bar{\mathbf{R }}\), if the consumption-direction vectors of agents \(g^i(\bar{\mathbf{R }}, f)\), \(i=1,\ldots , N\), are independent, and if \(f^i(\bar{\mathbf{R }})\in int A\), then agent i’s option set is the \(L-1\)-dimensional smooth surface of a strictly convex set in a neighborhood of \(f^i(\bar{\mathbf{R }})\) as illustrated in Fig. 1.
Instead of the independence of the consumption-direction vectors that is impossible when \(N>L\), we focus on a preference profile where all agents except two agents have partially identical preferences and they have the same consumption-direction vector. Without loss of generality, we assume agents \(i\ge 3\) are such agents. Let \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\) be a preference profile such that \(\bar{R}^i\), \(i\ge 3\), are identical in a cone Q and their consumption bundles \(f^i(\bar{\mathbf{R }})\), \(i\ge 3\), assigned by f are in Q or zero. Therefore they have the same consumption-direction vector \(g^3(\bar{\mathbf{R }},f)\) in Q. We suppose that the three consumption-direction vectors \(g^i(\bar{\mathbf{R }}, f)\), \(i=1,2,3\), are all different: \(g^i(\bar{\mathbf{R }},f)\ne g^j(\bar{\mathbf{R }},f)\) for any \(i,j\in \{1,2,3\}\) such that \(i\ne j\). We fix the preference of agent \(i\ge 3\) as \(\bar{R}^i\). We let \(Q^1\) and \(Q^2\) be cones in \({\mathcal{Q}}\) such that \(g^i(\bar{\mathbf{R }}, f)\in Q^i\), \(i=1,2\), respectively, and suppose that the social choice function f is pseudo-efficient and strategy-proof on \({{\mathcal{R}}}(\bar{R}^1, Q^{1c})\times{{\mathcal{R}}}(\bar{R}^2, Q^{2c})\times \{\bar{R}^3\}\times \cdots \times \{\bar{R}^N\}\). In this paper, we study the option set for agent \(i=1,2\), defined as
The fact that we omit the domain \({{\mathcal{R}}}(\bar{R}^i, Q^{ic})\) in the notation of \(G^i(\bar{\mathbf{R }}^{-i})\) should not cause any confusion. We are interested in the option set in a neighborhood of the consumption bundle \(f^i(\bar{\mathbf{R }})\), and the option set around the consumption bundle does not depend on the domain as long as the targeted preference profile \(\bar{\mathbf{R }}\) is included in \({{\mathcal{R}}}(\bar{R}^1, Q^{1c})\times{{\mathcal{R}}}(\bar{R}^2, Q^{2c})\times \{\bar{R}^3\}\times \cdots \times \{\bar{R}^N\}\).
We assume \(f^i(\bar{\mathbf{R }})\in int A\) for both \(i=1,2\). Under these assumptions, we can show that the option set is the \(L-1\)-dimensional smooth surface of a strictly convex set, as illustrated in Fig. 1, in a neighborhood of the consumption bundle \(f^i(\bar{\mathbf{R }})\) for \(i=1,2\).
Proposition 1
Let\(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\)be a preference profile such that\(\bar{R}^i\), \(i\ge 3\), are identical to\(\bar{R}^3\)in a cone\(Q\in{\mathcal{Q}}\)and\(g^3(\bar{\mathbf{R }},f)\in Q\). Let\(Q^i\in{\mathcal{Q}}\), \(i=1,2\), be cones such that\(g^i(\bar{\mathbf{R }},f)\in Q^i\)andfbe a social choice function that is pseudo-efficient and strategy-proof on\({{\mathcal{R}}}(\bar{R}^1, Q^{1 c})\times{{\mathcal{R}}} (\bar{R}^2,Q^{2c})\times \{\bar{R}^3\}\times \cdots \times \{\bar{R}^N\}\). Suppose that the consumption-direction vectors\(g^i(\bar{\mathbf{R }},f)\), \(i=1,2,3\), are different and\(f^i(\bar{\mathbf{R }})\in int A\)for both\(i=1,2\). Then, for\(i=1,2\), in a neighborhood of\(f^i(\bar{\mathbf{R }})\), the option set\(G^i(\bar{\mathbf{R }})\)is the\(L-1\)-dimensional smooth surface of a strictly convex set.
See Appendix for the proof of Proposition 1. The proof is essentially the same as that in Momi (2017) that established the same result for agent i’s option set, who receives consumption in intA, under the assumption that a social choice function is pseudo-efficient and strategy-proof in a neighborhood of \(\bar{\mathbf{R }}\) and the consumption-direction vectors are independent at \(\bar{\mathbf{R }}\). The following two points should be noted.
First, although the independence of the consumption-direction vectors ensures the determinacy of allocation, Momi (2017) needed only the determinacy of consumption among two agents who receive positive consumption to prove the topological property of the option set. In Proposition 1, the determinacy of consumption among agents 1 and 2 is ensured by the difference of consumption-direction vectors among agents 1, 2, and 3 and the equality of them for agents \(i\ge 3\).
Second, when Momi (2017) changed the preferences in a neighborhood of \(\bar{R}^i\) for agents \(i=1,2\), what mattered was the binary relations of the preferences in a neighborhood of the consumption bundle \(f^i(\bar{\mathbf{R }})\). As in Lemma 1, for any preference \(R^i\) sufficiently close to \(\bar{R}^i\), we can construct a preference \(\hat{R}^i\) that is identical to \(R^i\) in a neighborhood of \(f^i(\bar{\mathbf{R }})\) and identical to \(\bar{R}^i\) outside \(Q^{i}\). Thus, we can transform all the preferences in Momi’s proof into preferences in our domain \({{\mathcal{R}}}(\bar{R}^i,Q^i)\) without affecting the results.
5 Proof of the theorem
Based on the topological property of the option set, we can show that agent 1 or agent 2 should receive zero consumption. This result is a counterpart of Proposition 6 in Momi (2017) that proved that all agents except one agent receive zero consumption under the assumption of independent consumption-direction vectors.
Proposition 2
Let\(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\)be a preference profile such that\(\bar{R}^i\), \(i\ge 3\), are identical to\(\bar{R}^3\)in a cone\(Q\in{\mathcal{Q}}\)and\(g^3(\bar{\mathbf{R }},f)\in Q\). Let\(Q^i\in{\mathcal{Q}}\), \(i=1,2\), be cones such that\(g^i(\bar{\mathbf{R }},f)\in Q^i\)andfbe a social choice function that is pseudo-efficient and strategy-proof on\({{\mathcal{R}}}(\bar{R}^1, Q^{1 c})\times{{\mathcal{R}}} (\bar{R}^2,Q^{2c})\times \{\bar{R}^3\}\times \cdots \times \{\bar{R}^N\}\). Suppose the consumption-direction vectors\(g^i(\bar{\mathbf{R }},f)\), \(i=1,2,3\), are different. Then, \(f^1(\bar{\mathbf{R }}) \in \{0,\Omega \}\) or \(f^2(\bar{\mathbf{R }})\in \{0,\Omega \}\).
Proof
Apply the proof of Momi (2017, Proposition 6) directly. Momi (2017) proved that the fact that the option set is the \(L-1\)-dimensional smooth surface of a strictly convex set in a neighborhood of \(f^i(\bar{\mathbf{R } })\) for agents \(i=1,2\), who receive positive consumption at \(\bar{\mathbf{R }}\), contradicts that f is pseudo-efficient and strategy-proof on \({\mathcal{B}} (\bar{R}^1)\times{\mathcal{B}}(\bar{R}^2)\times \{\bar{R}^3\} \times \cdots \times \{\bar{R}^N\}\), where \({\mathcal{B}} (\bar{R}^i)\subset{{\mathcal{R}}}\) is a neighborhood of \(\bar{R}^i\).
We take the neighborhood \({\mathcal{B}}^i(\bar{R}^i)\) to be sufficiently small and transform each preference \(R^i\in{\mathcal{B}}(\bar{R}^i)\), \(i=1,2\), used in Momi’s proof to a preference \(\hat{R}^i\) that is identical to \(R^i\) in a neighborhood of \(f^i(\bar{\mathbf{R }})\) and identical to \(\bar{R}^i\) in \(Q^{ic}\), as shown in Lemma 1. For the preferences in Momi’s proof, what matters is their binary relations in a neighborhood of \(f^i(\bar{\mathbf{R }})\). Therefore, the transformations do not affect the result of the proof. That is, the contradiction is induced using agents 1 and 2’s preferences identical to \(\bar{R}^1\) and \(\bar{R}^2\) in \(Q^{1c}\) and \(Q^{2c}\), respectively.
This establishes that in the present proposition, the fact that the option set \(G^i(\bar{\mathbf{R }})\) is the \(L-1\) dimensional smooth surface of a strictly convex set in a neighborhood of \(f^i(\bar{\mathbf{R }})\) for agent \(i=1,2\) contradicts that f is pseudo-efficient and strategy-proof on \({{\mathcal{R}}}(\bar{R}^1, Q^{1 c})\times{{\mathcal{R}}}(\bar{R}^2,Q^{2c})\times \{\bar{R}^3\} \times \cdots \times \{\bar{R}^N\}\). \(\square\)
We consider a pair of a preference \(R^{*}\in{{\mathcal{R}}}\) and a cone \(Q^{*}\in \mathcal{Q}\) such that
where \(\bar{p}\) is the gradient vector of \(R^{*}\) at y: \(\bar{p}=p(R^{*},y)\). Figure 2 describes a pair of \(R^{*}\) and \(Q^{*}\) satisfying this condition. The existence of such a pair is observed as follows. Fix any \(R^{*}\) and pick a positive vector y on the ray \([\Omega ]\): \(y\in [\Omega ]\). Then \(\Omega -[y]\) equals \([\Omega ]\) in A and it intersects with \(\Omega /N+\bar{p}^\perp\) at \(\Omega /N\), which is in intA, The property holds for any vector \(y'\) in a neighborhood of y, and hence we have a desired cone \(Q^{*}\) as the union of such rays \([y']\). Note that if \(R^{*}\) and \(Q^{*}\) satisfies (1), then the preference \(R^{*}\) and any smaller cone \(Q'\subset Q^{*}\) also satisfies the condition.
Here, we explain what the condition (1) means. We consider a preference profile \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots , \bar{R}^N)\), where every preference \(\bar{R}^i\) is identical to \(R^{*}\) in \(Q^{*}\) and replace an agent’s preference with a linear preference that is represented by a linear utility function \(u(x)=\bar{p}x\). Such a linear preference is not an element of \({\mathcal{R}}\), and in the formal proof we use a preference in \({{\mathcal{R}}}\) whose upper contour set is sufficiently close to the upper contour set of the linear preference in \(R_+^L\). For an explanatory purpose, suppose that f is defined for the linear preference as a Pareto-efficient and strategy-proof social choice function.
Since \(\bar{p}\) is the gradient vector of \(R^{*}\) at \(y\in Q^{*}\) and all preferences are identical to \(R^{*}\) in \(Q^{*}\), the consumption of other agents at a Pareto-efficient allocation after one agent’s preference is replaced with the linear preference should be on the ray [y] or on the boundary of A. That is, the consumption of the agent whose preference is replaced should be on \(\Omega -[y]\) or on the boundary of A, which is shown as a bold segment in Fig. 2. As \(\sum _{i=1}^N f^i(\bar{\mathbf{R }})=\Omega\), there exists an agent whose original consumption \(f^i(\bar{\mathbf{R }})\) is on the upper right-hand side of the hyperplane \(\Omega /N+\bar{p}^\perp\). We replace this agent’s preference with the linear preference. Then, the agent’s new consumption should be on the upper right-hand side of the hyperplane \(f^i(\bar{\mathbf{R }})+\bar{p}^\perp\) because of the strategy-proofness of f. Therefore, the condition (1) ensures that the agent’s new consumption is on \(\Omega -[y]\), not on the boundary of A except the case in which he receives \(\Omega\) before and after the preference replacement.
The next proposition is the core of the proof of the theorem. It shows that we can increase the number of agents whose preferences are partially identical while one of them receives positive consumption.
Proposition 3
Let\(f:{{\mathcal{R}}}^N\rightarrow X\)be a pseudo-efficient and strategy-proof social choice function and\(R^{*} \in{{\mathcal{R}}}\)and\(Q^{*}\in{\mathcal{Q}}\)be a pair of a preference and a cone satisfying (1). Suppose that there exist a preference profile\(\bar{\mathbf{R }}=(\bar{R}^1, \ldots ,\bar{R}^N)\)andKagents, \(i_1,\ldots , i_K\), where\(K<N\), such that\(\bar{R}^{i_k}\in{{\mathcal{R}}}(R^{*}, Q^{*})\), \(k=1,\ldots ,K\), and\(f^{i_{k'}}(\bar{\mathbf{R }})\in int A\)for some\(k'\le K\). Then, there exist a preference profile\(\tilde{\mathbf{R }}=(\tilde{R}^1,\ldots ,\tilde{R}^N)\), \(K+1\)agents, \(j_1,\ldots , j_{K+1}\), and a cone\(\tilde{Q}\subset Q^{*}\)such that\(\tilde{R}^{j_k}\in{{\mathcal{R}}} (R^{*},\tilde{Q})\), \(k=1,\ldots ,K+1\), and\(f^{j_{k'}}(\tilde{\mathbf{R }})\in int A\)for some\(k'\le K+1\).
Proof
We suppose that there exist a preference profile \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\) and K agents, \(i_1,\ldots , i_K\), where \(K<N\), such that \(\bar{R}^{i_k}\in{{\mathcal{R}}}(R^{*},Q^{*})\), \(k=1,\ldots ,K\), and \(f^{i_{k'}}(\bar{\mathbf{R }})\in int A\) for some \(k'\le K\). Let \(Q'\) be a smaller cone included in \(Q^{*}\): \(Q'\subset Q^{*}\). If \(R'\in{{\mathcal{R}}}(R, Q^{*})\) for preferences \(R'\) and R, then \(R'\in{{\mathcal{R}}}(R, Q')\). Moreover, the pair of \(R^{*}\) and \(Q'\) satisfies (1). Therefore, without loss of generality, we assume \(\overline{Q^{*}}\) does not include \([\Omega ]\setminus \{0\}\) by taking \(Q^{*}\) smaller if needed.
If there exists an agent \(j\notin \{i_1,\ldots ,i_K\}\) such that \(f^j(\bar{\mathbf{R }})\in int A\), then let \(j=i_{K+1}\) and replace the agent’s preference \(\bar{R}^{i_{K+1}}\) with any preference \(R^{i_{K+1}}\) that is identical to \(R^{*}\) in \(Q^{*}\).Footnote 4 Then, \(f^{i_{K+1}}( R^{i_{K+1}},\bar{\mathbf{R }}^{-i_{K+1}})\in int A\) because of the strategy-proofness of f, and \(K+1\) agents’ preferences \(\bar{R}^{i_1},\ldots , \bar{R}^{i_K}\), and \(R^{i_{K+1}}\) are all identical to \(R^{*}\) in \(Q^{*}\). Thus, we have the desired result. Therefore, we assume \(f^j(\bar{\mathbf{R }})=0\) for any \(j\notin \{i_1,\ldots ,i_K\}\); that is, \(\sum _{k=1}^Kf^{i_k}(\bar{\mathbf{R }})=\Omega\).
We pick a vector \(y\in Q^{*}\) and let \(\bar{p}\) denote the gradient vector of \(R^{*}\) at y: \(\bar{p}=p( R^{*},y)\). Since the preferences \(\bar{R}^{i_k}\), \(k=1,\ldots ,K,\) are all identical to \(R^{*}\) in \(Q^{*}\), \(\bar{p}\) is the gradient vector at y for any \(\bar{R}^{i_k}\), \(k=1,\ldots , K\). To put it conversely, for any preferences \(\bar{R}^{i_k}\), \(k=1,\ldots , K\), the consumption-direction vectors for the price vector \(\bar{p}\) are the same and the vector is on the ray [y].
Since \(\sum _{k=1}^Kf^{i_k}(\bar{\mathbf{R }})=\Omega\), there exists an agent \(i_{k}\) whose consumption, \(f^{i_k}(\bar{\mathbf{R }})\), is in the upper right-hand side of the hyperplane \(\Omega /K+\bar{p}^\perp\). Without loss of generality, we assume \(i_1\) is such an agent. We construct agent \(i_1\)’s preference \(R^{i_1}_n\), whose upper contour sets converge to the upper contour sets of the linear preference represented by the linear utility function \(u(x)=\bar{p}x\) in \(R_{+}^L\) as \(n\rightarrow \infty\), as follows using the technique that Momi (2017) used and we use repeatedly in this proof.
We define \(E=\{x\in R_+^L: \bar{p}x\ge \bar{p}f^{i_1}(\bar{\mathbf{R }})\}\), which is the upper contour set of the linear preference at \(f^{i_1}(\bar{\mathbf{R }})\). This cannot be an upper contour set of a preference in \({{\mathcal{R}}}\). First, we modify it into a smooth set. Let \(\bar{D}_{1/n}\) denote a closed ball in \(R_+^L\) with radius 1/n and define \(E_n\) as the union of such closed balls included in E: \(E_n=\bigcup _{\bar{D}_{1/n} \subset E} \bar{D}_{1/n}\). \(E_n\) is not a strictly convex set. We modify \(\partial E_n\) into the surface of a strictly convex set so that it is an indifference set of a preference in \({{\mathcal{R}}}\). We let \(L'(z)\) denote the half line starting from z and extending in the direction of \(\bar{p}\): \(L'(z)=\{x\in R^L: x=z+t\bar{p}, t\ge 0\}\). We pick any preference \(\dot{R}\in{{\mathcal{R}}}\) whose gradient vector at \(f^{i_1}(\bar{\mathbf{R }})\) is \(\bar{p}\) and define
We define \(R_n^{i_1}\in{{\mathcal{R}}}\) as the preference that has \(I_n\) as its indifference set. See Lemmas A1 and A2 in Momi (2017) for the proof that \(I_n\) is well defined as an indifference set. From the construction, \(I_n\) converges to the boundary of E as \(n\rightarrow \infty\).
We replace \(\bar{R}^{i_1}\) with \(R_n^{i_1}\) and increase n. Because of the compactness of the feasible allocation set, there exists a convergent subsequence \(\{f^{i_1}(R^{i_1}_{n_h}, \bar{\mathbf{R }}^{-i_1})\}_{h=0}^\infty\) of agent \(i_1\)’s consumption, where \(n_h\rightarrow \infty\) as \(h\rightarrow \infty\). We let \(\bar{y}\) denote the limit of this convergent sequence: \(\bar{y} =\lim _{h\rightarrow \infty }f^{i_1}(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\). We consider two cases \(\bar{y}\in int A\) and \(\bar{y}\in \partial A\) separately.
Case 1. We consider the case \(\bar{y}\in int A\). Then, \(\bar{p}\) is the limit of the price vector: \(\bar{p}=\lim _{h\rightarrow \infty }p((R^{i_1}_{n_k},\bar{\mathbf{R }}^{-i_1}),f)\).
We construct agent \(i_1\)’s new preference \(\hat{R}^{i_1}\in{{\mathcal{R}}}\) and a cone \(\hat{Q} \subset Q^{*}\) such that \(p(\hat{R}^{i_1},\bar{y})=\bar{p}\), \(\hat{R}^{i_1}\in{{\mathcal{R}}}(\bar{R}^{i_1},\hat{Q})\), and the ratio of the distance between y and \(\hat{Q}\) to the distance between \(\hat{Q}\) and \(\partial Q^{*}\) measured on the hyperplane \(y+\bar{p}^\perp\) defined as
is arbitrarily small. As the denominator of (2) is bounded above, the condition requires that \(\hat{Q}\) can be arbitrarily close to y, while it is away from the boundary of \(Q^{*}\) with some distance. Keep in mind that \(\hat{R}^{i_1}\in{{\mathcal{R}}}(\bar{R}^{i_1},\hat{Q})\) means \(\hat{R}^{i_1}\in{{\mathcal{R}}}(R^{*},\hat{Q})\) because \(\bar{R}^{i_1}\in{{\mathcal{R}}}(R^{*},Q^{*})\) and \(\hat{Q}\subset Q^{*}\).
For example, such a preference and a cone are obtained as follows. Figure 3 depicts the construction. We let \(\tilde{y}\in [y]\) be the vector that is most preferred on the hyperplane \(\bar{y}+\bar{p}^\perp\) with respect to \(\bar{R}^{i_1}\); that is, \(UC(\tilde{y};\bar{R}^{i_1})\bigcap (\bar{y}+\bar{p}^\perp )=\tilde{y}\). Because of the strict convexity of the preference, we can pick \(\hat{y}\in I(\tilde{y};\bar{R}^{i_1})\) arbitrarily close to \(\tilde{y}\) such that \(\hat{y}\in Q^{*}\) and \(\bar{y}\) is in the upper right-hand side of the hyperplane \(\hat{y}+\hat{p}^\perp\), where \(\hat{p}\) is the gradient vector of \(\bar{R}^{i_1}\) at \(\hat{y}\): \(\hat{p}=p(\bar{R}^{i_1},\hat{y})\). We let \(\bar{D}_\epsilon (\bar{y})\subset R^L_{++}\) denote the closed ball with center \(\bar{y}\) and radius \(\epsilon\) and define K as the convex hull of the union of this ball and the upper contour set of \(\bar{R}^{i_1}\) at \(\tilde{y}\):
We fix the radius \(\epsilon\) so small that the ball \(\bar{D}_\epsilon (\bar{y})\) is in the upper right-hand side of the hyperplane \(\hat{y}+\hat{p}^\perp\), and hence \(\hat{y}\) is on the surface of K. We slightly modify \(\partial K\) into the surface of a strictly convex set. We pick any positive vector \(\alpha \in R_{++}^L\) and consider the hyperplane \(\alpha ^\perp\) passing through the origin and perpendicular to the vector \(\alpha\). We let L(z) denote the half line starting from z and extending in the direction of \(\alpha\): \(L(z)=\{x\in R^L: x=z+t\alpha , t\ge 0\}\). With a sufficiently small positive scalar s, we define
and we fix s so small that the intersection between \([\bar{y}]\) and I is strictly in the lower left-hand side of \(\bar{y}+\bar{p}^\perp\): \(\parallel [\bar{y}]\bigcap I\parallel <\parallel \bar{y}\parallel\). Note that we have \(\hat{y}\) on the set I because \(\hat{y}\) is on both \(I(\tilde{y};\bar{R}^{i_1})\) and \(\partial K\). We let \(R\in{{\mathcal{R}}}\) be the preference that has I as its indifference set. See Lemmas A1 and A3 in Momi (2017) for the proof that the set I is well defined as an indifference set.
Then, we pick \(\check{y}\) on \([\bar{y}]\) between \([\bar{y}]\bigcap I\) and \(\bar{y}\): \(\parallel [\bar{y}]\bigcap I\parallel<\parallel \check{y}\parallel <\parallel \bar{y}\parallel\). We let \(\check{R}\in{{\mathcal{R}}}\) be a preference that has the gradient vector \(\bar{p}\) at \(\check{y}\): \(p(\check{R}, \check{y})=\bar{p}\), and \(\hat{y}\) is strictly preferred to \(\check{y}\) with respect to \(\check{R}\). Then, \(\check{y}\in P(\hat{y};R)\) and \(\hat{y}\in P(\check{y}; \check{R})\).
The union set \(UC(\hat{y};R)\bigcap UC(\check{y}; \check{R})\) is not smooth. We modify it into a smooth set as follows. We let \(\bar{D}_\epsilon\) denote a closed ball with sufficiently small radius \(\epsilon\) and define F as the union of such closed balls included in the union set: \(F=\bigcup _{\bar{D}_\epsilon \subset UC(\hat{y};R)\bigcap UC(\check{y}; \check{R})}\bar{D}_\epsilon\). We define \(\hat{R}^{i_1}\) as the preference that has F as its upper contour set. See Lemma A2 in Momi (2017) for the proof that F is well defined as an upper contour set.
From the construction, \(\check{y}\) and \(\hat{y}\) are on the surface of F, and hence \(\hat{R}^{i_1}\) is identical to \(\check{R}\) in a neighborhood of \(\check{y}\) and identical to R in a neighborhood of \(\hat{y}\). We fix a cone \(Q'\) such that \(\{y,\hat{y}\} \subset Q'\subset Q^{*}\) and \(\overline{Q'}\setminus \{0\}\subset Q^{*}\), and chose a cone \(\hat{Q}\) satisfying \(\hat{y}\in \hat{Q}\subset Q'\) such that \(\hat{R}^{i_1}\) and \(\bar{R}^{i_1}\) are identical in \(\hat{Q}\). The distance between \(\hat{Q}\) and \(\partial Q^{*}\) measured on \(y+\bar{p}^\perp\) is larger than the fixed distance between \(Q'\) and \(\partial Q^{*}\) measured on \(y+\bar{p}^\perp\). As \(\hat{y}\) can be taken arbitrarily close to \(\tilde{y}\), the cone \(\hat{Q}\) constructed as explained above can be arbitrarily close to y. Thus, the ratio (2) can be arbitrarily small. This ends the construction of the desired \(\hat{R}^{i_1}\) and \(\hat{Q}\).
Now, at the preference profile \((\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})\), it holds that \(f^{i_1}(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})=\bar{y}\) and \(p((\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1}),f)=\bar{p}\). Then, \(g^{i_k}((\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1}),f)\in Q^{*}\) for \(k=2,\ldots , K\), and agents \(i_2,\ldots ,i_k\) have the same consumption-direction vector. If there exists an agent \(j\notin \{i_1,\ldots ,i_K\}\) such that \(f^j(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})\in int A\), then we have the desired result by letting \(j=i_{K+1}\) and replacing his preference \(\bar{R}^{i_{K+1}}\) with any preference identical to \(R^{*}\) in \(\hat{Q}\). Therefore, we assume there is no such agent; that is, \(\sum _{k=1}^Kf^{i_k}(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})=\Omega\). As \(f^{i_1}(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})=\bar{y}\in int A\), there exists another agent who receives positive consumption. Without loss of generality, we assume agent \(i_2\) is such an agent: \(f^{i_2}(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})\in int A\). We write \(\bar{y}^2=f^{i_2}(\hat{R}^{i_1},\bar{\mathbf{R }}^{i_2})\). Note that \(\bar{y}^2\) is on the ray [y].
We construct agent \(i_2\)’s new preference \(\hat{R}^{i_2}\) satisfying the following properties. When \(\bar{R}^{i_2}\) is replaced with another preference \(\hat{R}^{i_2}\), the agent’s consumption \(f^{i_2}(\hat{R}^{i_1},\hat{R}^{i_2},\bar{\mathbf{R }}^{-\{i_1,i_2\}})\) should be preferred to \(\bar{y}^2\) with respect to \(\hat{R}^{i_2}\) and should not be strictly preferred to \(\bar{y}^2\) with respect to \(\bar{R}^{i_2}\) because of the strategy-proofness of f. That is, the agent’s new consumption bundle should be in \(UC(\bar{y}^2;\hat{R}^{i_2})\bigcap LC(\bar{y}^2;\bar{R}^{i_2})\). We construct agent \(i_2\)’s new preference \(\hat{R}^{i_2}\) such that (i) \(\hat{R}^{i_2}\in{{\mathcal{R}}}(\bar{R}^{i_2},\hat{Q})\), (ii) \(g(\hat{R}^{i_2},x)\ne g(\bar{R}^{i_2},x)\) for any \(x\notin \overline{\hat{Q}}\), (iii) \(UC(\bar{y}^2;\hat{R}^{i_2})\bigcap LC(\bar{y}^2;\bar{R}^{i_2})\subset Q^{*}\), and (iv) for any gradient vector of \(\hat{R}^{i_2}\) at \(x\in UC(\bar{y}^2;\hat{R}^{i_2})\bigcap LC(\bar{y}^2;\bar{R}^{i_2})\), the corresponding consumption-direction vector of \(\bar{R}^{i_2}\) is in \(Q^{*}\): \(g(\bar{R}^{i_2}, p(\hat{R}^{i_2},x))\in Q^{*}\) for any \(x\in UC(\bar{y}^2;\hat{R}^{i_2})\bigcap LC(\bar{y}^2;\bar{R}^{i_2})\). Keep in mind \(\hat{R}^{i_2}\in{{\mathcal{R}}}(\bar{R}^{i_2},\hat{Q})\) means \(\hat{R}^{i_2}\in{{\mathcal{R}}}(R^{*}, \hat{Q})\).
For example, such a preference \(\hat{R}^{i_2}\) can be constructed as depicted in Fig. 4. We let \(\bar{D}_\epsilon\) denote a closed ball with radius \(\epsilon\) and F denote the union of such balls included in \(UC(\bar{y}^2;\bar{R}^{i_2})\) and tangent to \(I(\bar{y}^2;\bar{R}^{i_2})\bigcap \overline{\hat{Q}}\). We let \(F'=F+R^L_+\). We construct a new preference as before. We pick any positive vector \(\alpha \in R_{++}^L\) and consider the hyperplane \(\alpha ^\perp\) passing through the origin and perpendicular to the vector \(\alpha\) and the half line starting from z and extending in the direction of \(\alpha\): \(L(z)=\{x\in R^L: x=z+t\alpha , t\ge 0\}\). With a sufficiently small positive scalar s, we define
and we let \(\hat{R}^{i_2}\in{{\mathcal{R}}}\) be the preference that has \(I'\) as its indifference set. Observe that \(\hat{R}^{i_2}\) satisfies (i)–(iv). It is clear from the construction that (i) and (ii) hold. When the ratio (2) is sufficiently small, \(\hat{Q}\) is sufficiently close to \(\bar{y}^2\), while it is away from the boundary \(\partial Q^{*}\) measured on some hyperplane. Then, \(UC(\bar{y}^2;\hat{R}^{i_2})\bigcap LC(\bar{y}^2;\bar{R}^{i_2})\) is sufficiently close to \(I(\bar{y}^2;\bar{R}^{i_2})\bigcap \overline{\hat{Q}}\) and away from the boundary \(\partial Q^{*}\), and hence (iii) and (iv) hold. This ends the construction of the desired \(\hat{R}^{i_2}\).
We write \(\hat{\mathbf{R }}=(\hat{R}^{i_1},\hat{R}^{i_2}, \bar{\mathbf{R }}^{-\{i_1,i_2\}})\) and let \(\hat{p}\) denote the price vector at this preference profile: \(\hat{p}=p(\hat{\mathbf{R }},f)\). If there exists an agent \(j\notin \{i_1,\ldots ,i_K\}\) such that \(f^j(\hat{\mathbf{R }})\in int A\), then we have the desired result by letting \(j=i_{K+1}\) and by replacing his preference \(\bar{R}^{i_{K+1}}\) with any preference identical to \(R^{*}\) in \(\hat{Q}\). Therefore, we assume there is no such agent; that is, \(\sum _{k=1}^Kf^{i_k}(\hat{\mathbf{R }})=\Omega\).
We observe that \(f^{i_1}(\hat{\mathbf{R }})\in int A\), \(f^{i_2}(\hat{\mathbf{R }})\in int A\), \(g^{i_k}(\hat{\mathbf{R }},f)\), \(k=1,2,3\), are different, and \(g^{i_k}(\hat{\mathbf{R }},f) =g^{i_3}(\hat{\mathbf{R }},f)\) for \(k\ge 3\).
First, as \(f^{i_2}(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1}) =\bar{y}^2\in int A\), we have \(f^{i_2}(\hat{\mathbf{R }})\in int A\) by the strategy-proofness of f with respect to agent \(i_2\). Furthermore, the strategy-proofness implies that \(f^{i_2}(\hat{\mathbf{R }})\in UC(\bar{y}^2;\hat{R}^{i_2})\bigcap LC(\bar{y}^2;\bar{R}^{i_2})\). Then, \(g(\bar{R}^{i_2},\hat{p})\in Q^{*}\) by (iv). Since \(\bar{R}^{i_2},\ldots , \bar{R}^{i_K}\) are all identical to \(R^{*}\) in \(Q^{*}\), their consumption-direction vectors for \(\hat{p}\) are the same. Therefore, \(g^{i_k}(\hat{\mathbf{R }} ,f)=g^{i_3}(\hat{\mathbf{R }},f)\in Q^{*}\) for \(k\ge 3\).
If \(g^{i_2}(\hat{\mathbf{R }},f)\) equals \(g^{i_3}(\hat{\mathbf{R }},f)\), then the consumption-direction vector is in \(\hat{Q}\) by (ii). As agents \(i_1\) and \(i_2\)’s preferences \(\hat{R}^{i_1}\) and \(\hat{R}^{i_2}\) are both identical to \(R^{*}\) in \(\hat{Q}\), this implies that all agents \(i_1,\ldots , i_K\) have the same consumption-direction vector in \(\hat{Q}\). As \([\Omega ]\setminus \{0\}\) is not in \(\hat{Q}\), this contradicts \(\sum _{i_1}^Kf^{i_k}(\hat{\mathbf{R }})=\Omega\). Therefore, \(g^{i_2}(\hat{\mathbf{R }},f)\ne g^{i_3}(\hat{\mathbf{R }},f)\).
Finally, recall that both consumption-direction vectors \(g^{i_2}(\hat{\mathbf{R }},f)\) and \(g^{i_3}(\hat{\mathbf{R }},f)\) are in \(Q^{*}\). As \([\Omega ]\setminus \{0\}\) is not in \(Q^{*}\), we cannot scale up \(g^{i_2}(\hat{\mathbf{R }},f)\) and \(g^{i_3}(\hat{\mathbf{R }},f)\) so that their sum equals \(\Omega\), This implies that \(f^{i_1}(\hat{\mathbf{R }})\ne 0\) and \(g^{i_1}(\hat{\mathbf{R }},f)\) is different from either \(g^{i_2}(\hat{\mathbf{R }},f)\) or \(g^{i_3}(\hat{\mathbf{R }},f)\) as desired.
We let \(Q^{i_1}\) and \(Q^{i_2}\) be sufficiently small cones such that \(f^{i_1}(\hat{\mathbf{R }})\in Q^{i_1}\) and \(f^{i_2}(\hat{\mathbf{R }})\in Q^{i_2}\), and consider replacing \(\hat{R}^{i_1}\) and \(\hat{R}^{i_2}\) with preferences in \({{\mathcal{R}}}(\hat{R}^{i_1}, Q^{i_1c})\) and \({{\mathcal{R}}}(\hat{R}^{i_2}, Q^{i_2c})\), respectively.
There exists \(\tilde{R}^{i_1}\in{{\mathcal{R}}}(\hat{R}^{i_1}, Q^{i_1c})\) and \(\tilde{R}^{i_2}\in{{\mathcal{R}} }(\hat{R}^{i_2}, Q^{i_2c})\) such that there exists an agent \(j\notin \{i_1,\ldots ,i_K\}\) who receives positive consumption at the preference profile \((\tilde{R}^{i_1},\tilde{R}^{i_2}, \bar{\mathbf{R }}^{-\{i_1,i_2\}})\): \(f^j(\tilde{R}^{i_1},\tilde{R}^{i_2},\bar{\mathbf{R }}^{-\{i_1,i_2\}})\in int A\). If there is no such pair of preferences, let \(\hat{f}\) denote the restriction of f to agents \(i_1,\ldots , i_K\) with the other agents’ preferences fixed at \(\bar{R}^j\), \(j\notin \{i_1,\ldots ,i_K\}\). Then, \(\hat{f}\) is a social choice function in the K-agent economy that is pseudo-efficient and strategy-proof on \({{\mathcal{R}}}(\hat{R}^{i_1},Q^{i_1c}) \times{{\mathcal{R}}}(\hat{R}^{i_2},Q^{i_2c})\times \{\bar{R}^{i_3}\}\times \cdots \times \{\bar{R}^{i_K}\}\) and at the preference profile \(\hat{\mathbf{R }}'=(\hat{R}^{i_1},\hat{R}^{i_2}, \bar{R}^{i_3},\ldots ,\bar{R}^{i_K})\), \(g^{i_k}(\hat{\mathbf{R }}', \hat{f})=g^{i_3}(\hat{\mathbf{R }}',\hat{f})\) for \(k\ge 3\), \(g^{i_k}(\hat{\mathbf{R }}',\hat{f})\), \(k=1,2,3\), are different, and \(\hat{f}^{i_k}(\hat{\mathbf{R }}')\ne 0\) for both \(k=1,2\). This contradicts Proposition 2.
Since \(Q^{i_1}\) and \(Q^{i_2}\) are sufficiently small, there exists a cone \(\tilde{Q}\subset \hat{Q}\bigcap Q^{i_1c}\bigcap Q^{i_2c}\). Now, we have the desired result by letting \(j=i_{K+1}\) and replacing \(\bar{R}^{i_{K+1}}\) with any preference that is identical to \(R^{*}\) in \(\tilde{Q}\).
Case 2. We consider the case \(\bar{y}\in \partial A\). We let h be sufficiently large so that \(y_h\equiv f^{i_1}(R^{i_1}_{n_h}, \bar{\mathbf{R }}^{-i_1})\) is sufficiently close to the boundary \(\partial A\).
We observe that there exists an agent \(j\notin \{i_1,\ldots , i_K\}\) such that \(f^j(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\in int A\). We suppose \(\sum _{k=1}^Kf^i(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1}) =\Omega\), and show a contradiction. Recall Fig. 2 and the explanation of the condition (1) following the figure.
Because of the strategy-proofness of f, \(y_h\) is in \(UC(f^{i_1}(\bar{\mathbf{R }});R^{i_1}_{n_h})\), and \(UC(f^{i_1}(\bar{\mathbf{R }});R^{i_1}_{n_h})\) is in the upper right-hand side of \(f^{i_1}(\bar{\mathbf{R }})+\bar{p}^\perp\) from the construction of \(R^{i_1}_{n}\). Since \(f^{i_1}(\bar{\mathbf{R }})\) is in the upper right-hand side of \(\Omega /N+\bar{p}\), (1) ensures that \(I(y^h;R^{i_1}_{n_h} )\bigcap (\Omega -[y])\in int A\). Thus, \(y_h\), which is sufficiently close to \(\partial A\) is not on \(\Omega -[y]\).
We define \(x_h^{i_k}=(f^{i_k}(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_k}) +\bar{p}^\perp )\bigcap [ y]\) for \(k=2,\ldots , K\), and \(\hat{x}_h^{i_1}=(y_h+\bar{p}^\perp )\bigcap (\Omega -[y])\). On the one hand, since \(\bar{p}\) is the gradient vector of \(\bar{R}^{i_k}\) at y, \(x^{i_k}_h\) is preferred to \(f^{i_k}(R^{i_1}_{n_h}, \bar{\mathbf{R }}^{-i_1})\) with respect to \(\bar{R}^{i_k}\) for any \(k=2,\ldots , K\), where the indifference holds if and only if \(f^{i_k}(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\) is on [y]. However, \(f^{i_k}(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\in [y]\) for some k implies \(f^{i_k}(R^{i_1}_{n_h}, \bar{\mathbf{R }}^{-i_1})\in [y]\) for any \(k=2,\ldots , K\) because all preferences have the same gradient vector \(\bar{p}\) at y. Then, \(y_h=f^{i_1}(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\) should be on \(\Omega -[y]\), which is a contradiction. Therefore, \(x^{i_k}_h\) is strictly preferred to \(f^{i_k}(R^{i_1}_{n_h}, \bar{\mathbf{R }}^{-i_1})\) with respect to \(\bar{R}^{i_k}\) for any \(k=2,\ldots , K\). On the other hand, for a sufficiently large h, the indifference set \(I(y_h; R^{i_1}_{n_h})\) is sufficiently close to the boundary of E. Therefore, \(\hat{x}^{i_1}\) is strictly preferred to \(y_h\) with respect to \(R^{i_1}_{n_h}\).
The allocation where agent \(i_1\) receives \(\hat{x}_h^{i_1}\), agent \(i_k\) receives \(x^{i_2}_{n_h}\), \(k=2,\ldots , K\), and the other agents receive nothing is feasible and this contradicts that \(f(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\) is a Pareto-efficient allocation. Thus, there exists an agent \(j\notin \{i_1,\ldots , i_K\}\) such that \(f^j(R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\in int A\)
We construct agent \(i_1\)’s new preference \(\hat{R}^{i_1}\) and a cone \(\hat{Q}\subset Q^{*}\) such that \(\hat{R}^{i_1}\) is an MMT of \(R^{i_1}_{n_h}\) at \(y_h\) and \(\hat{R}^{i_1}\in{{\mathcal{R}}} (\bar{R}^{i_1},\hat{Q})\) as we did in Case 1.
We let \(\tilde{y}\) denote the most preferred consumption bundle in \(I(y_h;R^{i_1}_{n_h})\) with respect to \(\bar{R}^{i_1}\). As \(I(y_h;R^{i_1}_{n_h})\) is sufficiently close to the boundary of E, \(\tilde{y}\) is determined uniquely and \(\tilde{y}\) is sufficiently close to [y] because \(p(\bar{R}^{i_1},y)=\bar{p}\). Because of the strict convexity of the preference \(\bar{R}^{i_1}\), we can pick \(\hat{y}\in I(\tilde{y};\bar{R}^{i_1})\) such that \(\hat{y}\in Q^{*}\) and \(y_h\) is in the upper right-hand side of the hyperplane \(\hat{y}+\hat{p}^\perp\), where \(\hat{p}\) is the gradient vector of \(\bar{R}^{i_1}\) at \(\hat{y}\). We let \(\bar{D}_\epsilon (y_h)\subset R_{++}^L\) denote the closed ball with center \(y_h\) and radius \(\epsilon\) and define K as the convex hull of the union of this closed ball and the upper contour set of \(\bar{R}^{i_1}\) at \(\tilde{y}\):
We fix the radius \(\epsilon\) so small that \(\hat{y}\) is on the surface of K. We modify \(\partial K\) into the surface of a strictly convex set. We pick any positive vector \(\alpha \in R_{++}^L\) and consider the hyperplane \(\alpha ^\perp\) passing through the origin and perpendicular to the vector \(\alpha\). We let L(z) denote the half line starting from z and extending in the direction of \(\alpha\): \(L(z)=\{x\in R^L: x=z+t\alpha , t\ge 0\}\). With a sufficiently small positive scalar s, we define
and we fix s so small that the intersection between \([y_h]\) and I is in the outside of \(UC(y_h;R^{i_1}_{n_h})\): \(\parallel [y_h]\bigcap I\parallel <\parallel y_h\parallel\). Note that we have \(\hat{y}\) on the set I because \(\hat{y}\) is on both \(I(\tilde{y};\bar{R}^{i_1})\) and \(\partial K\). We let \(R\in{{\mathcal{R}}}\) be a preference that has I as its indifference set.
We pick a preference \(\check{R}\in{{\mathcal{R}}}\) such that \(\check{R}\) is an MMT of \(R^{i_1}_{n_h}\) at \(y_h\), \(\check{R}\) is sufficiently close to \(R^{i_1}_{n_h}\), and \(\hat{y}\) is strictly preferred to \(y_h\) with respect to \(\check{R}\). Then, \(y_h\in P(\hat{y};R)\) and \(\hat{y}\in P(y_h;\check{R})\).
The union set \(UC(\hat{y};R)\bigcap UC(y_h;\check{R})\) is not smooth. We modify it into a smooth set. We let \(\bar{D}_\epsilon\) denote a closed ball with sufficiently small radius \(\epsilon\) and define F as the union of such closed balls included in the union set: \(F=\bigcup _{\bar{D}_\epsilon \subset UC(\hat{y};R)\bigcap UC(y_h;\check{R})}\bar{D}_\epsilon\). We define \(\hat{R}^{i_1}\) as the preference that has F as its upper contour set.
From the construction, \(\check{y}\) and \(\hat{y}\) are on the surface of F, and hence \(\hat{R}^{i_1}\) is identical to \(\check{R}\) in a neighborhood of \(y_h\) and identical to R in a neighborhood of \(\hat{y}\). Since \(\check{R}\) is an MMT of \(R^{i_1}_{n_h}\) at \(y_h\), \(\hat{R}^{i_1}\) is also an MMT of \(R^{i_1}_{n_h}\) at \(y_h\). We pick a cone \(\hat{Q}\subset Q^{*}\) so that \(\hat{y}\in \hat{Q}\). This end the construction of the desired \(\hat{R}^{i_1}\) and \(\hat{Q}\).
We observe that there exists an agent \(j\notin \{i_1,\ldots ,i_K\}\) who receive positive consumption at the preference profile \((\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})\): \(f^j(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})\in int A\). As \(\hat{R}^{i_1}\) is an MMT of \(R^{i_1}_{n_h}\) at \(y_h\), we have \(f^{i_1}(\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1})=f^{i_1} (R^{i_1}_{n_h},\bar{\mathbf{R }}^{-i_1})\equiv y_h\) and \(p((\hat{R}^{i_1},\bar{\mathbf{R }}^{-i_1}),f) =p((R_{n_h}^{i_1},\bar{\mathbf{R }}^{-i_1}),f)\). An allocation is Pareto efficient if and only if the consumption assigned to agents sum to the total endowment and the gradient vectors of agents receiving positive consumption coincide. Thus, a Pareto-efficient allocation is Pareto efficient in the economy without agents receiving zero consumption. We assume \(f^j(\hat{R}^{i_1}, \bar{\mathbf{R }}^{-i_1})=0\) for any agent \(j\notin \{i_1, \ldots ,i_K\}\). Then, \((f^{i_1}(\hat{R}^{i_1}, \bar{\mathbf{R }}^{-i_1}),\ldots , f^{i_K}(\hat{R}^{i_1}, \bar{\mathbf{R }}^{-i_1}))\) is a Pareto-efficient allocation at the preference profile \((\hat{R}^{i_1},\bar{R}^{i_2},\ldots , \bar{R}^{i_K})\) in the K-agent economy consisting of agents \(i_1,\ldots , i_K\) . Then, this allocation is also Pareto efficient in the K-agent economy for the preference profile \((R^{i_1}_{n_h},\bar{R}^{i_1},\ldots , \bar{R}^{i_K})\). However, this contradicts the fact we proved: at an allocation \(f(R^{i_1}_{n_h},\bar{\mathbf{R }}^{i_1})\), where \(y_h\equiv f^{i_1}(R^{i_1}_{n_h},\bar{\mathbf{R }}^{i_1})\) is sufficiently close to \(\partial A\), there should exist an agent \(j\notin \{i_1,\ldots ,i_K\}\) such that \(f^j(R_{n_h}^{i_1}, \bar{\mathbf{R }}^{-i_1})\in int A\). Therefore, there exists an agent \(j\notin \{i_1,\ldots ,i_K\}\) such that \(f^j(\hat{R}^{i_1}, \bar{\mathbf{R }}^{-i_1})\in int A\)
We have the desired result of the proposition by letting \(j=i_{K+1}\) and replacing the agent’s preference \(\bar{R}^{i_{K+1}}\) with any preference \(R^{i_{K+1}}\) that is identical to \(R^{*}\) in \(\hat{Q}\). \(\square\)
We now prove the theorem. We prove that if a social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is pseudo-efficient and strategy-proof, then \(f^i(\mathbf{R })\in \{0,\Omega \}\) for any agent i and any \(\mathbf{R }\in{{\mathcal{R}}}^N\). We suppose that two agents receive positive consumption at a preference profile \((R^1,\ldots , R^N)\), and show a contradiction. We fix a pair of a preference \(R^{*}\in{{\mathcal{R}}}\) and a cone \(Q\in{{\mathcal{R}}}\) satisfying (1). First, we replace the preference of an agent who receives positive consumption with \(R^{*}\). Then, we increase the number of agents whose preferences are partially identical to \(R^{*}\) in a (smaller) cone in Q by applying Proposition 3 repeatedly. Thus, we finally reach a preference profile \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\) and a cone \(Q^{*}\subset{\mathcal{Q}}\) such that \(R^i\in{{\mathcal{R}}}(R^{*}, Q^{*})\), \(i=1,\ldots , N\), and some agent receives consumption in intA. We apply the discussion in the proof of Proposition 3 one final time.
Since \(\sum _{i=1}^Nf^i(\bar{\mathbf{R }})=\Omega\), there exists an agent i whose consumption, \(f^{i}(\bar{\mathbf{R }})\), is in the upper right-hand side of the hyperplane \(\Omega /N+\bar{p}^\perp\). Without loss of generality, we assume agent 1 is such an agent.
We pick a vector \(y\in Q^{*}\) such that \(y\notin [\Omega ]\) and let \(\bar{p}\) be the gradient vector of \(R^{1}\) at y: \(\bar{p}=p(\bar{R}^{1},y)\). Since the preferences \(\bar{R}^{i}\), \(i=1,\ldots ,N\), are all identical in Q, \(\bar{p}\) is the gradient vector at y for any \(\bar{R}^{i}\), \(i=1,\ldots , N\).
We construct agent 1’s preference \(R^{1}_n\) whose upper contour sets converge to the upper contour sets of the linear preference represented by the linear utility function \(u(x)=\bar{p}x\) in \(R_{+}^L\) as \(n\rightarrow \infty\) as we did in the proof of Proposition 3. Because of the compactness of the feasible allocation set, there exists a convergent subsequence \(\{f^{1}(R^{1}_{n_h},\bar{\mathbf{R }}^{-i_1})\}_{h=0}^\infty\) of agent 1’s consumption. We let \(\bar{y}\) denote the limit of this convergent sequence: \(\bar{y}=\lim _{h\rightarrow \infty }f^{1}(R^{1}_{n_h},\bar{\mathbf{R }}^{-1})\).
When \(\bar{y}\in \partial A\), \(f^1(R^1_{n_h},\bar{\mathbf{R }}^{-1})\) is sufficiently close to the boundary \(\partial A\). However, such allocation cannot be Pareto efficient among the N agents as we observed for K agents in Case 2 in the proof of Proposition 3.
We consider the case in which \(\bar{y}\in int A\). Then, \(\bar{p}\) is the limit of the price vector: \(\bar{p}=\lim _{h\rightarrow \infty }p((R^{1}_{n_k}, \bar{\mathbf{R }}^{-1}),f)\). We proceed as we did in Case 1 in the proof of Proposition 3.
We construct agent 1’s new preference \(\hat{R}^{1}\) and a cone \(\hat{Q} \subset Q^{*}\) such that \(p(\hat{R}^{1},\bar{y}) =\bar{p}\), \(\hat{R}^{1}\in{{\mathcal{R}}}(\bar{R}^{1},\hat{Q})\), and the ratio of the distance between y and \(\hat{Q}\) to the distance between \(\hat{Q}\) and \(\partial Q^{*}\) measured on the hyperplane \(y+\bar{p}^\perp\) is sufficiently small.
Then, \(f^{1}(\hat{R}^{1},\bar{\mathbf{R }}^{-1})=\bar{y}\), \(p((\hat{R}^{1},\bar{\mathbf{R }}^{-1}),f)=\bar{p}\), and hence \(g^{i}((\hat{R}^{1},\bar{\mathbf{R }}^{-1}),f)\in Q^{*}\) for \(i=2,\ldots , N\). Without loss of generality, we assume \(f^{2}(\hat{R}^{1},\bar{\mathbf{R }}^{-1})\in int A\). We write \(\bar{y}^2= f^{2}(\hat{R}^{1},\bar{\mathbf{R }}^{-1})\).
We construct agent 2’s new preference \(\hat{R}^{2}\) such that (i) \(\hat{R}^{2}\in{{\mathcal{R}}}(\bar{R}^{2},\hat{Q})\), (ii) \(g(\hat{R}^{2},x)\ne g(\bar{R}^{2},x)\) for any \(x\notin \overline{\hat{Q}}\), (iii) \(UC(\bar{y}^2;\hat{R}^{2})\bigcap LC(\bar{y}^2;\bar{R}^{2})\subset Q^{*}\), and (iv) for any gradient vector of \(\hat{R}^{2}\) at \(x\in UC(\bar{y}^2; \hat{R}^{2})\bigcap LC(\bar{y}^2;\bar{R}^{2})\), the corresponding consumption-direction vector of \(\bar{R}^{2}\) is in \(Q^{*}\): \(g(\bar{R}^{2}, p(\hat{R}^{2},x))\in Q^{*}\) for any \(x\in UC(\bar{y}^2;\hat{R}^{2})\bigcap LC(\bar{y}^2;\bar{R}^{2})\).
We write \(\hat{\mathbf{R }}=(\hat{R}^1,\hat{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})\). We have \(f^{1}(\hat{\mathbf{R }})\in int A\), \(f^{2}(\hat{\mathbf{R }})\in int A\), \(g^{i} (\hat{\mathbf{R }},f)\), \(i=1,2,3\), are different, and \(g^{i}(\hat{\mathbf{R }},f)=g^{3}(\hat{\mathbf{R }},f)\) for \(i\ge 3\) as we observed in the proof of Proposition 3. This contradicts Proposition 2. This ends the proof of the theorem.
6 Proof of the corollary
In the proof of the theorem, we established that if a social choice function \(f:{{\mathcal{R}}}^N\rightarrow X\) is pseudo-efficient and strategy-proof, then \(f^i(\mathbf{R })\in \{0,\Omega \}\) for any agent \(i=1,\ldots ,N\) and any \(\mathbf{R }\in{{\mathcal{R}}}^N\). As Pareto efficiency implies pseudo-efficiency, this result is slightly stronger than the statement of the theorem. We prove the corollary by repeatedly applying this result.
We let \(f:\bar{{\mathcal{R}}}^N\rightarrow X\) be a Pareto-efficient and strategy-proof social choice function defined on a domain \(\bar{{\mathcal{R}}}^N\) where \({{\mathcal{R}}}\subset \bar{{\mathcal{R}}}\subset{{\mathcal{R}}}_C\). As in the case of \(\mathbf{R }\in{{\mathcal{R}}}^N\), as mentioned in Sect. 3, \(f^i(\mathbf{R })\in int A\bigcup \{0,\Omega \}\) for any agent i and any preference profile \(\mathbf{R }\in \bar{{\mathcal{R}}}^N\). Therefore, all we have to prove is that \(f^i(\mathbf{R })\notin int A\) for any agent i and any \(\mathbf{R }\in \bar{{\mathcal{R}}}^N\). We suppose that \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\in \bar{{\mathcal{R}}}^N\) is a preference profile where an agent receives consumption in intA, and show a contradiction.
We let \(\mathbf{R }^{*}=(R^{1*},\ldots ,R^{N*}) \in{{\mathcal{R}}}^N\) be a preference profile in \({{\mathcal{R}}}^N\). We repeat the replacement of the preferences of agents who receive positive consumption as follows. We first pick an agent \(i_1\) who receives consumption in intA at \(\bar{\mathbf{R }}\). We replace his preference with \(R^{i_1*}\). Let \({\mathbf{R }}'=(R^{1\prime },\ldots ,R^{N\prime })\) denote the new preference profile after this replacement: \(R^{i_1\prime } =R^{i_1*}\) and \(R^{i\prime }=\bar{R}^i\) for \(i\ne i_1\). As agent \(i_1\)’s consumption at \(\mathbf{R }'\) is neither 0 nor \(\Omega\), there exists another agent \(i_2\) who receives positive consumption in intA at \(\mathbf{R }'\). We replace this agent’s preference with \(R^{i_2*}\) and let \(\mathbf{R }^{\prime \prime }\) denote the preference profile after this replacement. Note that agent \(i_2\)’s consumption at \(\mathbf{R }''\) is neither 0 nor \(\Omega\).
Then, we consider the replacement of agent \(i_1\)’s and agent \(i_2\)’s preferences with any preferences in \({{\mathcal{R}}}\). As a result of the replacement, there should exist a preference profile \(\tilde{\mathbf{R }}''=(\tilde{R}^{1\prime \prime },\ldots , \tilde{R}^{N\prime \prime })\) where \(\tilde{R}^{i_1\prime \prime }\in{{\mathcal{R}}}\), \(\tilde{R}^{i_2\prime \prime }\in{{\mathcal{R}}}\), \(\tilde{R}^{i\prime \prime }=\bar{R}^i\) for \(i\notin \{i_1,i_2\}\), and there exists another agent \(i_3\), different from \(i_1\) and \(i_2\), receiving positive consumption in intA at \(\tilde{\mathbf{R }}''\). If such a preference profile does not exist, then let \(f''\) be the social choice function f restricted to agents \(i_1\) and \(i_2\), with the other agents’ preferences fixed to \(\bar{R}^i\), \(i\notin \{i_1,i_2\}\). Then, \(f''\) is a social choice function in the two-agent economy of agents \(i_1\) and \(i_2\) that is Pareto efficient and strategy-proof on \({{\mathcal{R}}}\times{{\mathcal{R}}}\) and allocates consumption in intA to both agents at \((R^{i_1*},R^{i_2*})\). This contradicts the alternate dictatorship result mentioned in the first paragraph of this section.
Now, we replace agent \(i_3\)’s preference with \(R^{i_3*}\) and let \(\mathbf{R }^{\prime \prime \prime }\) denote the preference profile after the replacement: \(R^{i_1\prime \prime \prime } =\tilde{R}^{i_1\prime \prime }\), \(R^{i_2\prime \prime \prime } =\tilde{R}^{i_1\prime \prime }\), \(R^{i_3\prime \prime \prime } =R^{i_3*}\), and \(R^{i\prime \prime \prime }=\bar{R}^i\) for \(i\notin \{i_1,i_2,i_3\}\). Note that agent \(i_3\)’s consumption at \(\mathbf{R }^{\prime \prime \prime }\) is neither 0 nor \(\Omega\). Then, we consider the replacement of the preferences of agents \(i_1\), \(i_2\), and \(i_3\) with any preferences in \({{\mathcal{R}}}\). As a result of the replacement, there exists a preference profile \(\tilde{\mathbf{R }}^{\prime \prime \prime }\) where \(\tilde{R}^{i\prime \prime \prime }\in{{\mathcal{R}}}\) for \(i\in \{i_1,i_2,i_3\}\), \(\tilde{R}^{i\prime \prime \prime }=\bar{R}^i\) for \(i\notin \{i_1,i_2,i_3\}\), and there exists a fourth agent \(i_4\notin \{i_1,i_2,i_3\}\) who receives consumption in intA at \(\tilde{\mathbf{R }}^{\prime \prime \prime }\). If such a preference profile does not exist, then let \(f'''\) be the social choice function f restricted to agents \(i_1\), \(i_2\), and \(i_3\), with the other agents’ preferences fixed to \(\bar{R}^i\), \(i\notin \{i_1,i_2,i_3\}\). Then, \(f'''\) is a social choice function in the three-agent economy of agents \(i_1\), \(i_2\), and \(i_3\) that is pseudo-efficient and strategy-proof on \({{\mathcal{R}}} \times{{\mathcal{R}}}\times{{\mathcal{R}}}\) and allocates positive consumption in intA to at least two agents at the preference profile \((R^{i_1\prime \prime \prime }, R^{i_2\prime \prime \prime }, R^{i_3\prime \prime \prime })\).Footnote 5 This contradicts the alternate dictatorship result mentioned in the first paragraph of this section.
We replace the fourth agent’s preference with \(R^{i_4*}\) and consider the replacement of these four agents’ preferences with any preferences in \({\mathcal{R}}\). Repeating this process, we finally obtain a preference profile in \({{\mathcal{R}}}^N\) where at least two agents have consumption in intA. This contradicts the theorem. This ends the proof of the corollary.
7 Concluding remarks
In this paper, we proved that a Pareto-efficient and strategy-proof social choice function is alternately dictatorial. This was conjectured for many-agent economies as a counterpart of the dictatorship result in two-agent economies. We clarified that the determinacy of consumption among two agents is sufficient for us to investigate the compatibility of allocations with the efficiency and strategy-proofness of the social choice function. As a preference profile where the determinacy holds, we focused on a preference profile where all agents except two agents have the same consumption-direction vector and this vector and the two agents’ consumption-direction vectors are different. We increased the number of such agents who have the same consumption-direction vector by replacing the agents’ preferences with partially identical preferences.
The alternately dictatorial result was proved for the set of classical, homothetic and smooth preferences and extended to a larger set of classical preferences. This is the strongest result thus far obtained for such a preference domain. In particular, alternate dictatorship, where all agents except one receiver of the total endowment have zero consumption, implies the incompatibility of Pareto efficiency and strategy-proofness with allocation restrictions by Serizawa (2002), Serizawa and Weymark (2003), and Momi (2013b).
In two-agent economies, the dictatorship result has been proved for domains of restricted preferences. In particular, Hashimoto (2008) and Momi (2013a) proved the result for the domain of Cobb–Douglas preferences. Whether the alternate dictatorship result holds for domains of restricted preferences in many-agent economies remains an open question. Note that MMTs play crucial roles throughout the proofs presented in this paper. If preferences are restricted to the Cobb–Douglas type, for example, then there is no such richness in the preference domain: no preference has an MMT in the domain. It would thus be an interesting and challenging question to ask whether we would have Pareto-efficient, strategy-proof and non-alternately dictatorial mechanisms in many-agent economies with such a “thin” preference domain.
Notes
For the vectors x and \(x'\) in \(R^L\), \(x>x'\) denote that \(x_l\ge x'_l\) for any \(l=1,\ldots , L\) and \(x\ne x'\).
Therefore, if R is continuous, strictly convex on \(R_{++}^L\), and strictly monotonic on \(R_{++}^L\), then \(UC(x;R)\subset R_{++}^L\) for any \(x\in R^L_{++}\) and the boundary \(\partial R_{+}^L\) is an indifference set.
When \(K=1\), there exists such an agent j because \(f^{i_1}(\bar{\mathbf{R }})\in int A\) implies that there exists another agent who receives positive consumption.
For example, suppose that \(f^{i_1}(\mathbf{R }^{\prime \prime \prime })\in int A\), \(f^{i_2}(\mathbf{R }^{\prime \prime \prime })=0\), \(f^{i_3}(\mathbf{R }^{\prime \prime \prime })\in int A\), and \(f^{i}(\mathbf{R }^{\prime \prime \prime })=0\), for \(i\notin \{i_1,i_2,i_3\}\). Then, agents \(i_1\), \(i_2\), and \(i_3\) may receive zero consumption without violating the strategy-proofness and Pareto efficiency of the social choice function f when agent \(i_2\)’s preference is replaced. To deal with this case, we proved the result so far with a pseudo-efficient social choice function.
For compact subsets A and B, the metric is defined as \(\max _{a\in A,b\in B}\parallel a-b\parallel\).
As in the proof of Lemma A2, if there exists an \(x\in \overline{G^1 (\bar{\mathbf{R }}^{-1})}\) that is strictly preferred to \(\bar{x}\) with respect to \(\bar{R}^1\), then there exists a \(\hat{x}\in G^1(\bar{\mathbf{R }}^{-1})\) that is strictly preferred to \(\bar{x}\) with respect to \(\bar{R}^1\).
Here, the proof differs from that of Lemma 4 in Momi (2017). When \(\bar{x}^1\) is indifferent to \(\tilde{x}^1\) with respect to \(R^1\), there exists another agent j such that \(\tilde{x}^j\) is strictly preferred to \(\tilde{x}^j\) with respect to \(\bar{R}^j\). Momi (2017, Lemma 4) could set \(j=2\) without loss of generality because all agents were symmetric. In the present proof, agent 2 and the other agents \(i\ge 3\) are asymmetric and the agent j might not be agent 2. What we can insist for agent 2 is only that \(\bar{x}^2\) is not indifferent to \(\tilde{x}^2\), as we will observe soon. Thus, as seen in the proof, we must consider Case 2, \(\bar{x}^2\) is strictly preferred to \(\tilde{x}^2\), as well as Case 1, \(\tilde{x}^2\) is strictly preferred to \(\bar{x}^2\), that Momi (2017) studied.
\(\overline{G^2(\hat{R}^1_\epsilon , \bar{\mathbf{R }}^{-\{1,2\}})}\) may have an edge at \(\hat{x}_\epsilon ^2\), and \(\check{x}_{\epsilon ,\epsilon '}\) may be \(\hat{x}_\epsilon ^2\).
\(\overline{G^2 (\bar{\mathbf{R }}^{-2})}\) may also have an edge at \(\bar{x}^2\) and \(x_n^{2\prime }\) may be \(\bar{x}^2\).
References
Barberà S, Jackson M (1995) Strategy-proof exchange. Econometrica 63:51–87
Goswami MP, Mitra M, Sen A (2014) Strategy-proofness and Pareto-efficiency in quasi-linear exchange economies. Theor Econ 9:361–381
Hashimoto K (2008) Strategy-proofness versus efficiency on the Cobb–Douglas domain of exchange economies. Soc Choice Welf 31:457–473
Hatfield JW (2009) Strategy-proof, efficient, and nonbossy quota allocations. Soc Choice Welf 33:505–515
Hurwicz L (1972) On informationally decentralized systems. In: McGuire C, Radner R (eds) Decision and organization. North-Holland, Amsterdam, pp 297–336
Ju B-G (2003) Strategy-proofness versus efficiency in exchange economies: general domain properties and applications. Soc Choice Welf 21:73–93
Kannai Y (1970) Continuity properties of the core of a market. Econometrica 38:791–815
Kato M, Ohseto S (2002) Toward general impossibility theorems in pure exchange economies. Soc Choice Welf 19:659–664
Momi T (2013a) Note on social choice allocation in exchange economies with Cobb–Douglas preferences. Soc Choice Welf 40:787–792
Momi T (2013b) Note on social choice allocation in exchange economies with many agents. J Econ Theory 148:1237–1254
Momi T (2017) Efficient and strategy-proof allocation mechanisms in economies with many goods. Theor Econ 12:1267–1306
Nicolò A (2004) Efficiency and truthfulness with Leontief preferences. A note on two-agent two-good economies. Rev Econ Des 8:373–382
Satterthwaite MA, Sonnenschein H (1981) Strategy-proof allocation mechanism at differentiable points. Rev Econ Stud 48:587–597
Schummer J (1997) Strategy-proofness versus efficiency on restricted domains of exchange economies. Soc Choice Welf 14:47–56
Serizawa S (2002) Inefficiency of strategy-proof rules for pure exchange economies. J Econ Theory 106:219–241
Serizawa S, Weymark JA (2003) Efficient strategy-proof exchange and minimum consumption guarantees. J Econ Theory 109:246–263
Zhou L (1991) Inefficiency of strategy proof allocation mechanisms in pure exchange economies. Soc Choice Welf 8:247–254
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by JSPS KAKENHI Grant Number JP26380250.
Appendix
Appendix
1.1 Proof of Lemma 1
For example, we construct \(\hat{R}\) as follows. Figure 5 depicts the construction. Fix a vector \(\bar{x}\in Q'\). For each \(y\in \partial Q\bigcap I(\bar{x};\bar{R})\), we consider the hyperplane \(y+p(\bar{R},y)^\perp\) that supports the upper contour set \(UC(\bar{x};\bar{R})\) at y and the space \(y+p(\bar{R},y)^\perp -R_{++}^L\) strictly on the lower left-hand side of the hyperplane. We define V as
That is, V is \(U(\bar{x};\bar{R})\bigcup Q\) whose subsets in the lower left-hand sides of the hyperplanes \(y+p(\bar{R};y)^\perp\) for \(y\in \partial Q\bigcap I(\bar{x};\bar{R})\) are cut off. Note that \(\partial V\) equals \(I(\bar{x};\bar{R})\) outside of Q. Further, \(\partial V\bigcap Q'\) is away from \(UC(\bar{x};\bar{R})\); that is, they have no intersection.
Proof of Lemma 1
We modify V into a smooth set by truncating its edge as follows. We let \(\bar{D}_\epsilon\) denote a closed ball with sufficiently small radius \(\epsilon\) and define \(V'\) as the union of such closed balls included in V:
See Lemma A2 in Momi (2017) for the proof that \(V'\) is a smooth set as desired. Clearly, \(\partial V'\) equals \(\partial V\) outside Q
However, \(V'\) is not a strictly convex set. We modify \(\partial V'\) into the surface of a strictly convex set so that it is an indifference set of a preference in \({{\mathcal{R}}}\). We pick any positive vector \(\alpha \in R_{++}^L\) and consider the hyperplane \(\alpha ^\perp\) passing through the origin and perpendicular to the vector \(\alpha\). We let L(z) denote the half line starting from z and extending in the direction of \(\alpha\): \(L(z)=\{x\in R^L: x=z+t\alpha , t\ge 0\}\). With a sufficiently small positive scalar s, we define
We let \(\tilde{R}\in{{\mathcal{R}}}\) be the preference that has I as its indifference set. See Lemma A1 in Momi (2017) for the proof that I is well defined as an indifference set. As \(I(\bar{x};\bar{R})\) equals \(\partial V'\) outside Q, I equals \(I(\bar{x};\bar{R})\) outside Q. In addition, \(I\bigcap \overline{Q'}\) is away from \(UC(\bar{x};\bar{R})\). We fix a vector \(\tilde{x}\in I\).
We pick \(\hat{x}=t\bar{x}\), where \(t<1\), so that \(I\bigcap \overline{Q'}\) has no intersection with \(UC(\hat{x};\bar{R})\). Clearly, we can pick such \(\hat{x}\) with t sufficiently close to 1 because \(I(\hat{x};\bar{R})\bigcap \overline{Q'}\) converges to \(I(\bar{x};\bar{R})\bigcap \overline{Q'}\) as \(t\rightarrow 1\) with respect to the standard metric introduced into the set of compact subsets of \(R^L\).Footnote 6
When a preference R is sufficiently close to \(\bar{R}\), \(I(\hat{x};R)\bigcap K\) is sufficiently close to \(I(\hat{x}; \bar{R})\bigcap K\) with any compact set K. Therefore, we set the preference R so close to \(\bar{R}\) that \(I(\hat{x}, R)\bigcap \overline{Q}\) has no intersection with \(UC(\bar{x};\bar{R})\) and \(I\bigcap \overline{Q'}\) has no intersection with \(UC(\hat{x};R)\).
We define
We observe W in Q and outside Q separately. In Q, W equals \(UC(\hat{x};R)\bigcap UC(\tilde{x};\tilde{R})\). In particular, \(I=I(\tilde{x}; \tilde{R})\) is away from \(UC(\hat{x}; R)\) in \(Q'\). Therefore, \(\partial W\) equals \(I(\hat{x};R)\) in \(Q'\); that is \(\partial W\bigcap Q'=I(\hat{x}; R)\bigcap Q'\). Outside Q, W equals \(UC(\tilde{x};\tilde{R})\). Therefore, \(\partial W\) equals \(I(\tilde{x};\tilde{R})\) outside Q. Thus, we have \(\partial W\bigcap Q^c=I(\tilde{x};\tilde{R})\bigcap Q^c=I(\bar{x};\bar{R})\bigcap Q^c\).
As this set W has the edge at the intersection of \(I(\hat{x}; R)\) and \(I(\tilde{x},\tilde{R})\) in \(Q\setminus Q'\), we slightly modify it into a smooth set by truncating the edge as we did for V. We let \(\bar{D}_\epsilon\) denote a closed ball with sufficiently small radius \(\epsilon\) and define \(W'\) as the union of such closed balls included in W:
We let \(\hat{R}\in{{\mathcal{R}}}\) be a preference that has \(W'\) as its upper contour set. When \(\epsilon\) is sufficiently small, \(W'\) equals W in \(Q'\bigcup Q^c\), and hence \(W'\) has the above-mentioned properties of W: \(\partial W'\bigcap Q'=I(\tilde{x};\tilde{R})\bigcap Q'\) and \(\partial W'\bigcap Q^c=I(\bar{x};\bar{R})\bigcap Q^c\). Thus, \(\hat{R}\) is identical to R in \(Q'\) and identical to \(\bar{R}\) in \(Q^c\) as desired.
1.2 Proof of Proposition 1
The proof is essentially the same as the proof in Momi (2017, Section 4). Although a slight logical difference is only in the proof of Lemma A3, we rewrite the whole proof. As explained after the statement of Proposition 1, we focus on the determinacy of consumption among agents 1 and 2, and transform the preferences in Momi’s proof into preferences in our domains using Lemma 1.
Throughout this section, we suppose the following conditions of the proposition: \(\bar{\mathbf{R }}=(\bar{R}^1,\ldots ,\bar{R}^N)\) is a preference profile such that \(\bar{R}^i\), \(i\ge 3\), are identical to \(\bar{R}^3\) in a cone \(Q\in{\mathcal{Q}}\); \(g^3(\bar{\mathbf{R }}, f)\in Q\); \(Q^i\in{\mathcal{Q}}\), \(i=1,2\), are cones such that \(g^i(\bar{\mathbf{R }},f)\in Q^i\); f is a social choice function pseudo-efficient and strategy-proof on \({{\mathcal{R}}}(\bar{R}^1, Q^{1 c})\times{{\mathcal{R}}}(\bar{R}^2,Q^{2c})\times \{\bar{R}^3\} \times \cdots \times \{\bar{R}^N\}\); the consumption-direction vectors \(g^i(\bar{\mathbf{R }},f)\), \(i=1,2,3\), are different; and \(f^i(\bar{\mathbf{R }})\in int A\) for both \(i=1,2\).
The next lemma, which is a counterpart of Lemma 2 in Momi (2017), is an immediate consequence of the difference of consumption-direction vectors.
Lemma A1
Consider preferences\(\tilde{R}^i, R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\), \(i=1,2\). Suppose\(g^i(\tilde{R}^1,\tilde{R}^2,\bar{\mathbf{R }}^{-\{1,2\}})\), \(i=1,2,3\), are different and\(g^i(\tilde{R}^1,\tilde{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})=g^3(\tilde{R}^1,\tilde{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})\)for\(i\ge 3\). For\(i,j \in \{1,2\}\), if\(f^i(\tilde{R}^1,\tilde{R}^2, \bar{\mathbf{R }}^{-\{1,2\}}) =f^i(\hat{R}^1,\hat{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})\ne 0\)and\(\tilde{R}^i\)and\(\hat{R}^i\)have the same gradient vector at the consumption bundle, then\(f^j(\tilde{R}^1,\tilde{R}^2, \bar{\mathbf{R }}^{-\{1,2\}}) =f^j(\hat{R}^1,\hat{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})\).
Proof
Without loss of generality, we let \(i=1\) and \(j=2\). For simplicity, we write \(\tilde{\mathbf{R }}=(\tilde{R}^1,\tilde{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})\) and \(\hat{\mathbf{R }} =(\hat{R}^1,\hat{R}^2,\bar{\mathbf{R }}^{-\{1,2\}})\). As \(f^1(\tilde{\mathbf{R }})=f^1(\hat{\mathbf{R }})\ne 0\), and \(\tilde{R}^1\) and \(\hat{R}^1\) have the same gradient vector at the consumption bundle, we have \(g^i(\tilde{\mathbf{R }},f) =g^i(\hat{\mathbf{R }},f)\) for all agents.
As the consumption of all agents at the preference profiles \(\tilde{\mathbf{R }}\) and \(\hat{\mathbf{R }}\), respectively, sum to \(\Omega\), we have \(\sum _{i=1}^Nf^i(\tilde{\mathbf{R }}) =\sum _{i=1}^N\parallel f^i(\tilde{\mathbf{R }})\parallel g^i(\tilde{\mathbf{R }},f)=\Omega\) and \(\sum _{i=1}^Nf^i (\hat{\mathbf{R }})=\sum _{i=1}^N\parallel f^i(\hat{\mathbf{R }}) \parallel g^i(\hat{\mathbf{R }},f)=\Omega\). Considering the difference between these equations, we have \((\parallel f^2(\tilde{\mathbf{R }})\parallel -\parallel f^2(\tilde{\mathbf{R }})\parallel )g^2(\tilde{\mathbf{R }},f)+(\sum _{i=3}^N\parallel f^i(\tilde{\mathbf{R }})\parallel -\sum _{i=3}^N\parallel f^i(\hat{\mathbf{R }})\parallel )g^3(\tilde{\mathbf{R }},f)=0\) because \(f^1(\tilde{\mathbf{R }})=f^1(\hat{\mathbf{R }})\), \(g^2(\tilde{\mathbf{R }},f)=g^2(\hat{\mathbf{R }},f)\) and \(g^i(\tilde{\mathbf{R }},f)=g^i(\tilde{\mathbf{R }},f)=g^3(\tilde{\mathbf{R }},f)\) for \(i\ge 3\). As the consumption-direction vectors of agents 2 and 3 are independent, we have \(\parallel f^2(\tilde{\mathbf{R }}) \parallel = \parallel f^2(\hat{\mathbf{R }})\parallel\), and hence \(f^2(\tilde{\mathbf{R }})=f^2(\hat{\mathbf{R }})\). \(\square\)
By the definition of the option set, \(f^i(\bar{\mathbf{R }})\) is the most preferred consumption bundle in the option set \(G^i(\bar{\mathbf{R }}^{-i})\) with respect to \(\bar{R}^i\) for \(i=1,2\). We want to establish the reverse: the most preferred consumption bundle in \(G^i(\bar{\mathbf{R }}^{-i})\) with respect to \(\bar{R}^i\) is \(f^i(\bar{\mathbf{R }})\). For tractability, we initially work with the closure of the option set, \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\). By considering the closure, we ensure the existence of the most preferred consumption vector in \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) with respect to any preference \(R^i\). The next lemma, which is a counterpart of Lemma 3 in Momi (2017), shows that if a consumption bundle is the most preferred in the closure of the option set with respect to some preference, then the consumption bundle is actually an element of the option set.
Lemma A2
For\(i=1,2\), if\(x\in Q^i\)is the most preferred consumption bundle in\(\overline{G^i(\bar{\mathbf{R }}^{-i})}\)with respect to\(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\), then\(x\in G^i(\bar{\mathbf{R }}^{-i})\).
Proof
We let \(\hat{R}^i\) be an MMT of \(R^i\) at x sufficiently close to \(R^i\). See Momi (2013b, Lemma 4) for the existence of such an MMT. Then, by applying Lemma 1, we let \(\check{R}^i\) be a preference that is identical to \(\hat{R}^i\) in a neighborhood of x and identical to \(R^i\) outside \(Q^i\). Thus, \(\check{R}^i\) is an MMT of \(R^i\) at x and an element of \({{\mathcal{R}}}(\bar{R}^i,Q^{ic})\). We show \(x=f^i(\check{R}^i, \bar{\mathbf{R }}^{-i})\). Since \(\check{R}^i\) is an MMT of \(R^i\) at x, \(UC(x;\check{R}^i)\setminus x\subset P(x;R^i)\). Therefore, x is the unique most preferred consumption bundle in \(\overline{G^i(\mathbf{R }^{-i})}\) with respect to \(\check{R}^i\).
As \(x\in \overline{G^i(\bar{\mathbf{R }}^{-i})}\), there exists a \(\hat{x}\in G^i(\bar{\mathbf{R }}^{-i})\) arbitrarily close to x. Therefore, if x is strictly preferred to \(f^i(\check{R}^i,\bar{\mathbf{R }}^{-i})\) with respect to \(\check{R}^i\), then \(\hat{x}\) is strictly preferred to \(f^i(\check{R}^i,\bar{\mathbf{R }}^{-i})\). This contradicts the strategy-proofness of f. Therefore, \(f^i(\check{R}^i, \bar{\mathbf{R }}^{-i})\in UC(x;\check{R}^i)\). Then, \(f^i(\check{R}^i,\bar{\mathbf{R }}^{-i})\ne x\) contradicts that x is the most preferred consumption bundle in \(\overline{G^i(\mathbf{R }^{-i})}\) with respect to \(\check{R}^i\). Hence, \(x=f^i(\check{R}^i,\bar{\mathbf{R }}^{-i})\in G^i(\bar{\mathbf{R }}^{-i})\). \(\square\)
An immediate consequence of Lemma A2 is that if x is the unique most preferred consumption bundle in \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) with respect to \(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\) for \(i=1,2\), then \(x=f^i(R^i,\bar{\mathbf{R }}^{-i})\). The next lemma, which is a counterpart of Lemma 4 in Momi (2017), shows that the most preferred consumption bundle is actually unique in a neighborhood of \(f^i(\bar{\mathbf{R }})\). Thus, for any preference \(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\), the most preferred consumption bundle in \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) with respect to the preference is unique, and it is exactly the consumption bundle \(f^i(R^i, \bar{\mathbf{R }}^{-i})\) allocated to the agent for the preference by the social choice function f.
Lemma A3
For\(i=1,2\), in a neighborhood of\(f^i (\bar{\mathbf{R }})\), \(f^i(\bar{\mathbf{R }})\)is the unique most preferred consumption bundle in\(\overline{G^i (\bar{\mathbf{R }}^{-i})}\)with respect to\(\bar{R}^i\).
Proof of Lemma A3: Case 1
Proof of Lemma A3: Case 2
Proof
The proof is slightly different from the proof of Lemma 4 in Momi (2017). Without loss of generality, we prove the statement for agent 1. We write \(f(\bar{\mathbf{R }})=\bar{\mathbf{x }} =(\bar{x}^1,\ldots ,\bar{x}^N)\) and \(\bar{p}=p(\bar{\mathbf{R }},f)\). From the definitions, \(\bar{x}^1\) is (one of) the most preferred consumption bundles in \(G^1(\bar{\mathbf{R }}^{-1})\) with respect to \(\bar{R}^1\), and no consumption bundle in \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) is strictly preferred to \(\bar{x}^1\) with respect to \(\bar{R}^1\).Footnote 7 We suppose that there exists another consumption bundle \(\tilde{x}^1\) in \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) that is indifferent to \(\bar{x}^1\) with respect to \(\bar{R}^1\), and show a contradiction. We define the gradient vector of \(\bar{R}^1\) at \(\tilde{x}^1\) as \(\tilde{p}\): \(\tilde{p}=p(\bar{R}^1, \tilde{x}^1)\).
Since we are interested in a neighborhood of \(\bar{x}^1\), we assume that \(\tilde{x}^1\) is sufficiently close to \(\bar{x}^1\) so that \(\tilde{x}^1\in Q^1\), \(g^2(\bar{R}^2,\tilde{p})\in Q^2\), \(g^3(\bar{R}^3,\tilde{p})\in Q\), and these vectors are different.
We let \(\check{R}^1\) be a preference that is identical to \(\bar{R}^1\) outside \(Q^1\), \(I(\bar{x}^1;\check{R}^1)\bigcap I(\bar{x}^1;\bar{R}^1)=\{\bar{x}^1,\tilde{x}^1\}\) and \(UC(\bar{x}^1;R) \subset UC(\bar{x}^1;\bar{R}^1)\). That is, both \(\bar{x}^1\) and \(\tilde{x}^1\) are the most preferred consumption bundles in \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) with respect to \(\check{R}^1\). Note that \(f^i(\check{R}^1,\bar{\mathbf{R }}^{-1})\) should be \(\bar{x}^1\) or \(\tilde{x}^1\) for such a preference \(\check{R}^1\). We assume that there exists such a preference \(\check{R}^1\) satisfying \(f^i(\check{R}^1,\bar{\mathbf{R }}^{-1}) =\bar{x}^1\). At the end of the proof, we see that this assumption does not lose generality.
Observe that the scalars a and b satisfying \(\tilde{x}^1+ag(\bar{R}^2, \tilde{p})+bg(R^3;\tilde{p})=\Omega\) are determined uniquely because the consumption-direction vectors of agents 2 and 3 are independent. We define \(\tilde{x}^2=ag(\bar{R}^2;\tilde{p})\) and \(x=bg(\bar{R}^3;\tilde{p})\) using the uniquely determined scalars.
Figure 6 describes the situation in which the closure of agent 1’s option set has the two most preferred consumption bundles \(\bar{x}^1\) and \(\tilde{x}^1\) with respect to the preference \(\bar{R}^1\). In the following proof, we observe that such an option set contradicts the pseudo-efficiency and strategy-proofness of the social choice function.
We construct agent 1’s new preferences \(R_t^1\) as follows. We pick \(\tilde{R}^1\), which is an MMT of \(\bar{R}^1\) at \(\tilde{x}^1\), and \(R^{1\prime }\), which is an MMT of \(\bar{R}^1\) at \(\bar{x}^1\). Let \(\epsilon >0\) be a sufficiently small scalar. For a parameter \(t\in (1-\epsilon ,1)\) sufficiently close to one, we define \(K_t\) as the convex hull of the set \(UC(t\tilde{x}^1; \tilde{R}^1)\bigcup UC(\bar{x}^1; R^{1\prime })\):
We set \(\epsilon\) sufficiently small so that for any \(t\in (1-\epsilon ,1)\), \(\tilde{p}\) and \(\bar{p}\) are normal vectors of the supporting hyperplanes to \(K_t\) at \(t\tilde{x}^1\) and \(\bar{x}^1\), respectively.
Applying Lemma A1 in Momi (2017) with \(K_t\), we slightly modify the indifference set \(I(\bar{x}^1;\bar{R}^1)\). We consider the hyperplane \((\tilde{x}^1)^\perp\) passing through the origin and perpendicular to the vector \(\tilde{x}^1\). For each \(y\in (\tilde{x}^1)^\perp\), we let L(y) denote the half line starting from y and extending in the direction of \(\tilde{x}^1\): \(L(y)=\{x\in R^L|x=y+r\tilde{x}^1, r\ge 0\}\). We fix a scalar \(\bar{s}<1\) close to one and define the following:
We let \(\tilde{R}_t^{1}\in{{\mathcal{R}}}\) be agent 1’s preference that has \(I_t\) as its indifference set. Note that \(\tilde{R}_t^{1}\) can be arbitrarily close to \(\bar{R}^1\) by setting \(\bar{s}\) close to one. We pick a cone \(Q'\) including both \(\bar{x}\) and \(\tilde{x}^1\) and \(\overline{Q'}\setminus \{0\}\subset Q^1\). We set \(\bar{s}\) sufficiently close to one and apply Lemma 1 so that we have a preference \(R^1_t\) that is identical to \(\tilde{R}^1_t\) in \(Q'\) and identical to \(\bar{R}^1\) outside \(Q^1\) for any \(t\in (1-\epsilon ,1)\).
Both \(R_t^{1}\) and \(\bar{R}^1\) have the same gradient vectors \(\tilde{p}\) and \(\bar{p}\) at \(\tilde{x}^1\) and \(\bar{x}^1\), respectively. Observe that \(R_t^{1}\) is an MMT of \(\bar{R}^1\) at \(\tilde{x}^1\). Furthermore, observe that \(UC(\bar{x}^1; R_t^{1})\bigcap LC(\bar{x}^1; \bar{R}^1)\) consists of the point \(\bar{x}^1\) and a set in a neighborhood of \(\tilde{x}^1\) that converges to \(\tilde{x}^1\) as t converges to 1.
We write \(f(R_t^{1},\bar{\mathbf{R }}^{-1})=\mathbf{x }_t =(x_t^{1},\ldots ,x_t^{N})\). These t in \(x_t^i\) should not be confused with the subscripts labeling goods. Since \(R_t^{1}\) is an MMT of \(\bar{R}^1\) at \(\tilde{x}^1\), \(x_t^{1}=\tilde{x}^1\). Therefore \(x_t^2=\tilde{x}^2\) and \(\sum _{i=3}^Nx_t^i=x\), as shown in Lemma A1.
We show that \(\tilde{x}^2\) is not indifferent to \(\bar{x}^2\) with respect to \(\bar{R}^2\).Footnote 8 We assume that \(\tilde{x}^2\) is indifferent to \(\bar{x}^2\) with respect to \(R^2\) and show a contradiction. Since the preferences of agents \(i\ge 3\) are all identical in Q, the consumption vectors \(\bar{x}^i\), \(i\ge 3\) are parallel and \(x_t^i\), \(i\ge 3\) are parallel. Therefore for \(i\ge 3\), their consumption bundles are written as \(\bar{x}^i=a^i\sum _{i=3}^N\bar{x}^i\) and \(x_t^i=b^i\sum _{i=3}^N x_t^i\) using the scalars \(a^i\) and \(b^i\), \(i=3,\ldots , N\), such that \(0\le a^i\le 1\), \(\sum _{i=3}^Na^i=1\), \(0\le b^i\le 1\), and \(\sum _{i=3}^Nb^i=1\). Using a scalar \(s\in (0,1)\), we set a new allocation \(x^{*}=(x^{1*},\ldots ,x^{N*})\) as follows: \(x^{1*}=s\bar{x}^1+(1-s)\tilde{x}^1\), \(x^{2*} =s\bar{x}^2+(1-s)\tilde{x}^2\), and for \(i\ge 3\)
Because of the strict convexity of the preferences, \(x^{1*}\) is preferred to either \(\bar{x}^i\) or \(x_t^i=\tilde{x}^i\) for agent \(i=1,2\). For agent \(i\ge 3\), as \(\bar{R}^i\) is identical to \(\bar{R}^3\) in Q, if \(\sum _{i=3}^N x_t^i\) is preferred to \(\sum _{i=3}^N\bar{x}^i\) with respect to \(\bar{R}^3\), then \(x^{i*}\) is preferred to \(\bar{x}^i=a^i\sum _{i=3}^N \bar{x}^i\). If \(\sum _{i=3}^N \bar{x}^i\) is preferred to \(\sum _{i=3}^N x_t^i\) with respect to \(\bar{R}^3\), then \(x^{i*}\) is preferred to \(x_t^i=b^i\sum _{i=3}^N x_t^i\). The feasibility of the allocation \(\mathbf{x }^{*}\) is clear from the fact that \(\sum _{i=3}^Nx^{*i}= s\sum _{i=3}^N \bar{x}^i+(1-s)\sum _{i=3}^N x_t^i\) and the feasibility of \(\bar{\mathbf{x }}\) and \(\mathbf{x }_t\). This contradicts the Pareto efficiency of the allocations \(\bar{\mathbf{x }}\) and \(\mathbf{x }_t\).
Now, we separate two cases depending on whether \(\tilde{x}^2\) is strictly preferred or strictly less preferred to \(\bar{x}^2\) with respect to \(R^2\)
Case 1. We consider the case in which \(\tilde{x}^2\) is strictly preferred to \(\bar{x}^2\) with respect to \(\bar{R}^2\). That is, there exists a positive vector \(\alpha \in R^{L}_{++}\) such that \(\tilde{x}^2 \in P(\bar{x}^2+\alpha ;\bar{R}^2)\). Figure 6 illustrates this case.
We pick \(\hat{R}^2\) such that (i) \(\hat{R}^2\) is an MMT of \(\bar{R}^2\) at \(\bar{x}^2\) and equivalent to \(\bar{R}^2\) outside \(Q^2\), (ii) \(\tilde{x}^{2} \in P(\bar{x}^2;\hat{R}^2)\), and (iii) \(g(\hat{R}^2, \tilde{p})\) is different from \(g(\bar{R}^2, \tilde{p})\).
Observe that \(f^2(\bar{R}^1, \hat{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\bar{x}^2\) because \(\hat{R}^2\) is an MMT of \(\bar{R}^2\) at \(\bar{x}^2\). Therefore, \(f^1(\bar{R}^1, \hat{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\bar{x}^1\), as shown in Lemma A1.
We write \(f(R_{t}^{1},\hat{R}^2,\bar{\mathbf{R }}^{-\{1,2\}}) =\hat{\mathbf{x }}_{t}=(\hat{x}_{t}^{1},\ldots ,\hat{x}_{t}^{N})\) and focus on \(\hat{x}_{t}^{1}\) with t sufficiently close to 1. Facing the other agents’ preferences \((\hat{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})\), agent 1 can achieve \(\bar{x}^1\) by reporting \(\bar{R}^1\), as mentioned above. Therefore, \(\hat{x}_{t}^{1}\) should be preferred to \(\bar{x}^1\) with respect to \(R_{t}^{1}\). On the contrary, \(\hat{x}_{t}^{1}\) is not strictly preferred to \(\bar{x}^1\) with respect to \(\bar{R}^1\). Therefore, \(\hat{x}_{t}^{1}\in UC(\bar{x}^1; R_{t}^{1})\bigcap LC(\bar{x}^1; \bar{R}^1)\). Recall that this set consists of the point \(\bar{x}^1\) and a set in a neighborhood of \(\tilde{x}^1\) that converges to \(\tilde{x}^1\) as t converges to 1. We investigate these two cases.
We consider the case in which \(\hat{x}_{t}^{1}=\bar{x}^1\). As \(R_{t}^{1}\) and \(\bar{R}^1\) have the same gradient vector at \(\bar{x}^1\), and \(\hat{R}^2\) and \(\bar{R}^2\) have the same gradient vector at \(\bar{x}^2\), this case implies that \(\hat{x}_{t}^{2}=\bar{x}^2\). Recall that \(f^2(R_{t}^{1}, \bar{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\tilde{x}^{2}\) and we have chosen \(\hat{R}^2\) so that \(\tilde{x}^2 \in P(\bar{x}^2; \hat{R}^2)\). If agent 2 has the preference \(\hat{R}^2\) and faces the other agents’ preferences \((R_{t}^{1}, \bar{\mathbf{R }}^{-\{1,2\}})\), he can become better off by reporting \(\bar{R}^2\) and achieving \(\tilde{x}^2\) than reporting his true preference \(\hat{R}^2\) and achieving \(\hat{x}^2_{t}=\bar{x}^2\). This contradicts the strategy-proofness of f.
We now consider the case in which \(\hat{x}_{t}^1\) is in a set in a neighborhood of \(\tilde{x}^1\) that converges to \(\tilde{x}^1\) as \(t\rightarrow 1\). In this case, as \(t\rightarrow 1\), the gradient vector of \(R_{t}^{1}\) at \(\hat{x}_{t}^{1}\) converges to \(\tilde{p}\). Therefore, the price vector at \(\hat{\mathbf{x }}_{t}\) converges to \(\tilde{p}\). In particular, the gradient of \(\hat{R}^2\) at \(\hat{x}_{t}^{2}\) converges to \(\tilde{p}\).
However, note the equation \(\hat{x}_{t}^{2}=\tilde{x}^2+\sum _{i\ne 2}(\tilde{x}^i-\hat{x}_{t}^{i})\) obtained from \(\sum _{i=1}^N\tilde{x}^i=\Omega\) and \(\sum _{i=1}^N\hat{x}_t^{i}=\Omega\). On the right-hand side of this equation, \(\tilde{x}^1-\hat{x}_{t}^{1}\rightarrow 0\) as \(t\rightarrow 1\). For agent \(i\ge 3\) all \(\tilde{x}^i\) are parallel and on \([g(R^3,\tilde{p})]\) and all \(x^i_{t}\) are also parallel and converge to consumptions on \([g(R^3,\tilde{p})]\). Since \(\hat{x}_{t}^{2}\) is different from \(\tilde{x}^2\) because of (iii), the limit of \(\sum _{i=3}^N\tilde{x}^i-\sum _{i=3}^N\hat{x}_{t_k}\) is written as \(ag(R^3,\tilde{p})\), where the scalar a is not zero.
If \(a>0\), then \(\hat{x}_{t}^2\) with sufficiently large t should be strictly preferred to \(\tilde{x}^2\) with respect to any preference. Then, agent 2 with the preference \(\bar{R}^2\) facing the other agents’ preferences \((R^1_{t}, \bar{\mathbf{R }}^{-\{1,2\}})\) can be better off by reporting \(\hat{R}^2\) and achieving \(\hat{x}_{t}^2\) than reporting his true preference \(\bar{R}^2\) and achieving \(\tilde{x}^2\). This contradicts the strategy-proofness of f.
If \(a<0\), then \(\tilde{x}^2\) should be strictly preferred to \(\hat{x}_{t}^2\) with sufficiently large t. Then, agent 2 with the preference \(\hat{R}^2\) facing the other agents’ preferences \((R^1_{t},\bar{\mathbf{R }}^{-\{1,2\}})\) can be better off by reporting \(\bar{R}^2\) and achieving \(\tilde{x}^2\) than reporting his true preference \(\hat{R}^2\) and achieving \(\hat{x}_{t}^2\). This contradicts the strategy-proofness of f.
Case 2. We consider the case in which \(\bar{x}^2\) is strictly preferred to \(\tilde{x}^2\) with respect to \(\bar{R}^2\). That is, there exists a positive vector \(\alpha \in R^{L}_{++}\) such that \(\bar{x}^2 \in P(\tilde{x}^2+\alpha ;\bar{R}^2)\). Figure 7 depicts this case.
Recall that we have assumed the existence of a preference \(\check{R}^1\) such that \(\check{R}^1\in{{\mathcal{R}}} (\bar{R}^1,Q^{1c})\), \(I(\bar{x}^1;\check{R}^1)\bigcap I(\bar{x}^1;\bar{R}^1)=\{\bar{x}^1,\tilde{x}^1\}\), \(UC(\bar{x}^1;\check{R}^1)\subset UC(\bar{x}^1;\bar{R}^1)\), and \(f^1(\check{R}^1,\bar{\mathbf{R }}^{-1})=\bar{x}^1\). Thus, \(f^2 (\check{R}^1,\bar{\mathbf{R }}^{-1})=\bar{x}^2\) as shown in Lemma A1.
We consider \(\check{R}^2\) such that (i) \(\check{R}^2\) is an MMT of \(\bar{R}^2\) at \(\tilde{x}^2\) and identical to \(\bar{R}^2\) outside \(Q^2\), (ii)\(\bar{x}^2\in P(\tilde{x}^2;\check{R}^2)\), and (iii) \(g(\check{R}^2,\bar{p})\ne g(\bar{R}^2,\bar{p})\).
Since \(f^2(R_t^1,\bar{\mathbf{R }}^{-1})=\tilde{x}^2\) and \(\check{R}^2\) is an MMT of \(\bar{R}^2\) at \(\tilde{x}^2\), we have \(f^2(R_t^1,\check{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\tilde{x}^2\), and hence \(f^1(R_t^1,\check{R}^2, \bar{\mathbf{R }}^{-\{1,2\}}) =\tilde{x}^1\), as shown in Lemma A1. We write \(f(\check{R}^1, \check{R}^2,\bar{\mathbf{R }}^{-\{1,2\}})=\check{\mathbf{x }} =(\check{x}^1,\ldots , \check{x}^N)\) and consider the location of \(\check{x}^1\).
Since \(f^1(R_t^1,\check{R}^2,\bar{\mathbf{R }}^{-\{1,2\}}) =\tilde{x}^1\) and \(f^1( \check{R}^1, \check{R}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\check{x}^1\), \(\check{x}^1\) should be preferred to \(\tilde{x}^1\) with respect to \(\check{R}^1\) and \(\tilde{x}^1\) should be preferred to \(\check{x}^1\) with respect to \(R_t^1\). Therefore, we have \(\check{x}^1\in UC(\tilde{x}^1;\check{R}^1)\bigcap LC(\tilde{x}^1;R^1_t)\) for any t. As \(t\rightarrow 1\), \(R^1_t\rightarrow \bar{R}^1\), and hence \(UC(\tilde{x}^1;\check{R}^1)\bigcap LC(\tilde{x}^1;R^1_t)\rightarrow UC(\tilde{x}^1;\check{R}^1)\bigcap LC(\tilde{x}^1;\bar{R}^1)=\{\bar{x}^1,\tilde{x}^1\}\). Therefore, \(\check{x}^1\) should be \(\tilde{x}^1\) or \(\bar{x}^1\).
Suppose \(\check{x}^1=\tilde{x}^1\). Then, \(\check{x}^2=\tilde{x}^2\), and agent 2 with the preference \(\check{R}^2\) facing the other agents’ preferences \((\check{R}^1, \bar{\mathbf{R }}^{-\{1,2\}})\) can be better off by reporting \(\bar{R}^2\) and achieving \(\bar{x}^2\) than reporting his true preference \(\check{R}^2\) and achieving \(\check{x}^2=\tilde{x}^2\). This contradicts the strategy-proofness of f.
Suppose \(\check{x}^1=\bar{x}^1\). We have \(\check{x}^2 =\bar{x}^2+\sum _{i=3}^N\bar{x}^i-\sum _{i=3}^N\check{x}^i\). All \(\bar{x}^i\) and \(\check{x}^i\) for \(i\ge 3\) are on the ray \([g(\bar{R}^3;\bar{p})]\). Furthermore, because \(\check{x}^2\ne \bar{x}^2\), as ensured by (iii), \(\sum _{i=3}^N\bar{x}^i -\sum _{i=3}^N\check{x}^i\ne 0\), Therefore, we can write \(\sum _{i=3}^N\bar{x}^i-\sum _{i=3}^N\check{x}^i=ag(\bar{R}^3;\bar{p})\) with a non-zero scalar a.
If \(a>0\), then \(\check{x}^2\) is strictly preferred to \(\bar{x}^2\) with any preference. Agent 2 with the preference \(\bar{R}^2\) facing the other agents’ preferences \((\check{R}^1, \bar{\mathbf{R }}^{-\{1,2\}})\) can be better off by reporting \(\check{R}^2\) and achieving \(\check{x}^2\) than reporting his true preference \(\bar{R}^2\) and achieving \(\bar{x}^2\). This contradicts the strategy-proofness of f.
If \(a<0\), then \(\bar{x}^2\) is strictly preferred to \(\check{x}^2\) with any preference. Agent 2 with the preference \(\check{R}^2\) facing other agents’ preferences \((\check{R}^1, \bar{\mathbf{R }}^{-\{1,2\}})\) can be better off by reporting \(\bar{R}^2\) and achieving \(\bar{x}^2\) than reporting his true preference \(\check{R}^2\) and achieving \(\check{x}^2\). This contradicts the strategy-proofness of f. This ends Case 2.
We proved that a preference \(\bar{R}^1\), such that \(f^1(\bar{\mathbf{R }})=\bar{x}^1\), does not have another consumption bundle \(\tilde{x}^1\in \overline{G^1(\bar{\mathbf{R }}^{-1})}\) indifferent to \(\bar{x}^1\) with respect to \(R^1\) under the assumption that there exists a preference \(\check{R}^1\) such that \(\check{R}^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\), \(I(\bar{x}^1;\check{R}^1)\bigcap I(\bar{x}^1;\bar{R}^1) =\{\bar{x}^1,\tilde{x}^1\}\), \(UC(\bar{x}^1;\check{R}^1)\subset UC(\bar{x}^1;\bar{R}^1)\), and \(f^1(\check{R}^1, \bar{\mathbf{R }}^{-1})=\bar{x}^1\).
Suppose that there exists no such preference \(\check{R}^1\). Then \(f^1(R,\bar{\mathbf{R }}^{-1})=\tilde{x}^1\) for any preference R such that \(R\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\), \(I(\bar{x}^1; R)\bigcap I(\bar{x}^1;\bar{R}^1)=\{\bar{x}^1,\tilde{x}^1\}\), \(UC(\bar{x}^1; R)\subset UC(\bar{x}^1;\bar{R}^1)\). We pick two such preferences \(R^{\prime 1}\) and \(R^{\prime \prime 1}\) satisfying \(UC(\bar{x}^1; R^{\prime \prime 1})\subset UC(\bar{x}^1;R^{\prime 1})\).
Replacing \(\bar{R}^1\), \(\bar{x}^1\), and \(\check{R}^1\) with \(R^{\prime 1}\), \(\tilde{x}^1\), and \(R^{\prime \prime 1}\), respectively, what we proved establishes that a preference \(R^{\prime 1}\), such that \(f^1(R^{\prime 1}, \bar{\mathbf{R }}^{-1})=\tilde{x}^1\), does not have another consumption bundle \(\bar{x}^1\in \overline{G^1 (\bar{\mathbf{R }}^{-1})}\) indifferent to \(\tilde{x}^1\) with respect to \(R^{\prime 1}\) because there exists the preference \(R^{\prime \prime 1}\) such that \(R^{\prime \prime 1}\in{{\mathcal{R}}}( R^{\prime 1},Q^{1c})\), \(I(\tilde{x}^1; R^{\prime \prime 1})\bigcap I(\tilde{x}^1; R^{\prime 1})=\{\bar{x}^1,\tilde{x}^1\}\), \(UC(\tilde{x}^1; R^{\prime \prime 1})\subset UC(\tilde{x}^1; R^{\prime 1})\), and \(f^1( R^{\prime \prime 1},\bar{\mathbf{R }}^{-1})=\tilde{x}^1\). This implies that \(\bar{x}^1\) and \(\tilde{x}^1\) are not indifferent with respect to \(\bar{R}^1\). Thus, a preference \(\bar{R}^1\) such that \(f^1(\bar{\mathbf{R }})=\bar{x}^1\) does not have another consumption bundle \(\tilde{x}^1\in \overline{G^1(\bar{\mathbf{R }}^{-1})}\) indifferent to \(\bar{x}^1\) with respect to \(\bar{R}^1\) regardless of the existence of the preference \(\check{R}^1\) we assumed. \(\square\)
The next proposition is a counterpart of Proposition 1 in Momi (2017) that showed that the social choice function \(f(\cdot ,\bar{\mathbf{R }})\) is a continuous function of \(R^i\) with the other agents’ preferences \(\bar{\mathbf{R }}^{-i}\) fixed. In our setup, agent 1’s consumption determines only agent 2’s consumption and the sum of the other agents’ consumption. The consumption bundles for agents \(i\ge 3\) themselves are indeterminate. Moreover, the efficiency and strategy-proofness of \(f(\cdot ,\bar{\mathbf{R }}^{-i})\) are assumed on \({{\mathcal{R}}}(\bar{R}^{i},Q^{ic})\) for \(i=1,2\), in our setup, while they are assumed in a neighborhood of \(\bar{R}^i\) in Momi (2017).
Proposition A1
For\(i,j\in \{1,2\}\), \(f^j(\cdot ,\bar{\mathbf{R }}^{-i})\)is a continuous function on the domain\({{\mathcal{R}}} (\bar{R}^i,Q^{ic})\).
Proof
Without loss of generality, we prove the proposition for \(i=1\). We only have to prove that if the consumption-direction vectors \(g(\bar{R}^i,p(\bar{\mathbf{R }},f))\), \(i=1,2,3\), are different at \(\bar{\mathbf{R }}\) and if \(f^1(\bar{\mathbf{R }})\in int A\), then \(f^j(\cdot , \bar{\mathbf{R }}^{-i})\), \(j\in \{1,2\}\) are continuous functions at \(\bar{R}^1\). Suppose that the claim is true and let \(R^1\) be a preference close to \(\bar{R}^1\). Then, \(f^1(R^i,\bar{\mathbf{R }}^{-i})\) is close to \(f^1(\bar{\mathbf{R }})\) because of the supposed continuity, and hence the price vectors are close at the preference profiles \((R^1,\bar{\mathbf{R }}^{-1})\) and \(\bar{\mathbf{R }}\). Then the consumption-direction vectors of agents 1,2,and 3 at the preference profile \(( R^i,\bar{\mathbf{R }}^i)\) are still independent and \(f^1( R^i,\bar{\mathbf{R }}^{-1})\in int A\). Then, \(f^j(\cdot ,\bar{\mathbf{R }}^{-i})\), \(j\in{1,2}\) are continuous at \(R^1\) because of the supposed claim.
We first prove that \(f^1(\cdot ,\bar{\mathbf{R }}^{-1})\) is a continuous function at \(\bar{R}^1\). We let \(\{R_n^{1}\}_{n=1}^\infty\) be a sequence of preferences identical to \(\bar{R}^1\) outside \(Q^1\) converging to \(\bar{R}^i\) as \(n\rightarrow \infty\). There exists a convergent subsequence \(\{f_{n_k}^1(R^{1},\bar{\mathbf{R }}^{-1})\}_{k=1}^\infty\) because of the compactness of the feasible allocation set. We write \(f^1(R_{n_k}^{1},\bar{\mathbf{R }}^{-1})\rightarrow x^{1*}\) as \(k\rightarrow \infty\). All we have to show is that \(x^{1*}=f^1(\bar{\mathbf{R }})\).
We observe that \(x^{1*}\) is indifferent to \(f^1(\bar{\mathbf{R }})\) with respect to \(\bar{R}^1\). If \(x^{1*}\in P(f^1(\bar{\mathbf{R }}); \bar{R}^1)\), then \(f^1(R_{n_k}^{1},\bar{\mathbf{R }}^{-1})\in P(f^1(\bar{\mathbf{R }}); \bar{R}^1)\) for a sufficiently large k. This contradicts the strategy-proofness of f. If \(f^1(\bar{\mathbf{R }})\in P(x^{1*};\bar{R}^1)\), then \(f^1(\bar{\mathbf{R }})\in P(f^1(R_{n_k}^{1},\bar{\mathbf{R }}^{-1}); R_{n_k}^{1})\) for a sufficiently large k because \(f^1(R_{n_k}^{1}, \bar{\mathbf{R }}^{-1})\) converges to \(x^{1*}\) as \(k\rightarrow \infty\) and \(UC(x; R_{n_k}^{1})\bigcap K\) converges to \(UC(x;\bar{R}^1)\bigcap K\) at any consumption x with a compact set K as \(k\rightarrow \infty\) with respect to the standard metric in the set of compact subsets of \(R^L\). Again, this contradicts the strategy-proofness of f. Thus, \(x^{1*}\) is indifferent to \(f^1(\bar{\mathbf{R }})\) with respect to \(\bar{R}^1\). On the contrary, \(x^{1*}\in \overline{G^1(\bar{\mathbf{R }}^{-1})}\) because \(f^1(R_{n_k}^{1},\bar{\mathbf{R }}^{-1})\in G^1(\bar{\mathbf{R }}^{-1})\) for any k. Then, \(x^{1*}=f^1(\bar{\mathbf{R }})\) by Lemma A3.
We now prove the continuity of \(f^2(\cdot ,\bar{\mathbf{R }}^{-1})\) at \(\bar{R}^1\). We have proved the continuity of \(f^1(\cdot ,\bar{\mathbf{R }})\) at \(\bar{R}^1\). That is, if \(\{R_n^{1}\}_{n=1}^\infty\) is a sequence of preferences converging to \(\bar{R}^1\) as \(n\rightarrow \infty\), then \(f^1(R_n^{1}, \bar{\mathbf{R }}^{-1})\) converges to \(f^1(\bar{\mathbf{R }})\). According to this convergence, the gradient vector of \(R_n^{1}\) at \(f^1(R_n^{1},\bar{\mathbf{R }}^{-1})\) converges to the gradient vector of \(\bar{R}^1\) at \(f^1(\bar{\mathbf{R }})\); that is, \(p((R_n^{1},\bar{\mathbf{R }}^{-1}),f)\) converges to \(p(\bar{\mathbf{R }},f)\), and hence, \(g^j((R_n^{1}, \bar{\mathbf{R }}^{-1}),f)\) converges to \(g^j(\bar{\mathbf{R }},f)\) for any agent j .
As in the proof of Lemma A1, \(f^j(\mathbf{R })=\parallel f^j(\mathbf{R }) \parallel g^j(\mathbf{R },f)\), and the sum of the agents’ consumption equals the total endowment. Thus, we have two equalities: \(f^1(\bar{\mathbf{R }})+ \parallel f^2(\bar{\mathbf{R }}) \parallel g^2(\bar{\mathbf{R }},f)+\parallel \sum _{i=3}^Nf^i(\bar{\mathbf{R }}) \parallel g^3(\bar{\mathbf{R }},f)=\Omega\) and \(f^1(R_n^{1}, \bar{\mathbf{R }}^{-1})+ \parallel f^2(R_n^{1},\bar{\mathbf{R }}^{-1}) \parallel g^2((R_n^{1},\bar{\mathbf{R }}^{-1}),f)+\parallel \sum _{i=3}^Nf^i(R_n^{1},\bar{\mathbf{R }}^{-1}) \parallel g^3((R_n^{1},\bar{\mathbf{R }}^{-1}),f)=\Omega\) for any n. Considering the difference between these equalities, we have:
As \(n\rightarrow \infty\), the first, third, and fifth elements in the last equation converge to zeros. As \(g^j(\bar{\mathbf{R }},f)\), \(j=2,3\), are independent vectors, \(\parallel f^2(R_n^{1},\bar{\mathbf{R }}^{-1}) \parallel\) converges to \(\parallel f^2(\bar{\mathbf{R }}) \parallel\). This implies that \(f^2(R_n^{1},\bar{\mathbf{R }}^{-1})\) converges to \(f^2(\bar{\mathbf{R }})\) as \(n\rightarrow \infty\). That is, \(f^2(\cdot , \bar{\mathbf{R }}^{-1})\) is continuous at \(\bar{R}^1\). \(\square\)
We can show that \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) is the surface of a convex set in the sense that in a neighborhood of \(f^i(\bar{\mathbf{R }})\), \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) is in the lower left-hand side of the hyperplane \(f^i (R^i,\bar{\mathbf{R }}^{-i})+p((R^i,\bar{\mathbf{R }}^{-i}),f)^\perp\) for any \(R^i\) in a neighborhood of \(\bar{R}^i\). The next proposition is a counterpart of Proposition 2 in Momi (2017).
Proposition A2
For any\(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\)in a neighborhood of\(\bar{R}^i\), \(i=1,2\), \(\overline{G^i(\bar{\mathbf{R }}^{-i})} \subset f^i(R^i, \bar{\mathbf{R }}^{-i})+p((R^i, \bar{\mathbf{R }}^{-i}),f))^\perp -R_{+}^L\)holds in a neighborhood of\(f^i(\bar{\mathbf{R }})\); that is, there exist positive scalars\(\bar{\epsilon }\)and\(\epsilon '\)such that
for any\(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\bigcap{\mathcal{B}}_{\epsilon '}(\bar{R}^i)\), where\(D_{\bar{\epsilon }} (f^i(\bar{\mathbf{R }}))\)is the open ball in\(R_+^L\)with center\(f^i(\bar{\mathbf{R }})\)and radius\(\bar{\epsilon }\)and\({\mathcal{B}}_{\epsilon '}(\bar{R}^i)\)is the open ball in\({{\mathcal{R}}}\)with center\(\bar{R}^i\)and radius\(\epsilon '\)
Proof
Without loss of generality, we show the result for \(i=1\). We first show that for any \(R^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) in a neighborhood of \(\bar{R}^1\), \(\overline{G^1(\bar{\mathbf{R }}^{-1})} \subset f^1(R^1, \bar{\mathbf{R }}^{-1})+p((R^1, \bar{\mathbf{R }}^{-1}),f))^\perp -R_{+}^L\) holds in a neighborhood of \(f^1(R^1,\bar{\mathbf{R }}^{-1})\). That is, there exists a positive scalar \(\epsilon _{R^1}\), depending on \(R^1\), such that:
All we have to show is the existence of an \(\epsilon _{\bar{R}^1}\) satisfying (4) at \(\bar{\mathbf{R }}\) where the consumption-direction vectors \(g^i(\bar{\mathbf{R }},f)\), \(i=1,2,3\), are different and \(f^i(\bar{\mathbf{R }})\in int A\) for both \(i=1,2\). Suppose this claim to be true. If \(R^1\in{{\mathcal{R}}} (\bar{R}^i,Q^{1c})\) is sufficiently close to \(\bar{R}^i\), then \(f^1(R^i,\bar{\mathbf{R }}^{-i})\) is sufficiently close to \(f(\bar{\mathbf{R }})\) by Proposition A1. Hence, the difference of consumption-direction vectors among agents 1,2, and 3 and positivity of consumption for agents 1 and 2 still hold at the preference profile \((R^1,\bar{\mathbf{R }}^{-1})\). Then, there exists an \(\epsilon _{R^1}\) satisfying (4) by the supposed claim.
Contrary to the existence of an \(\epsilon _{\bar{R}^1}\) satisfying (4), we suppose that \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\) has an intersection with \(f^1(\bar{\mathbf{R }})+ p(\bar{\mathbf{R }},f)^\perp +R_{++}^L\) in any neighborhood of \(f^1(\bar{\mathbf{R }})\). Then, there exists a preference in a neighborhood of \(\bar{R}^1\) that has the two most preferred consumption bundles in \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\). See Momi (2017, Proposition 2) for an example of such a preference \(R^1_{\epsilon ,t(\epsilon )}\) that converges to \(\bar{R}^1\) as \(\epsilon \rightarrow 0\). Further, one of the two most preferred consumption bundles in \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\) with respect to \(R^1_{\epsilon ,t (\epsilon )}\) is \(f^1(\bar{\mathbf{R }})\) and the other is in a neighborhood of \(f^1(\bar{\mathbf{R }})\). Applying Lemma 1, we construct a new preference \(\tilde{R}^1_{\epsilon ,t(\epsilon )}\) that is identical to \(R^1_{\epsilon ,t(\epsilon )}\) in a neighborhood of \(f^1(\bar{\mathbf{R }})\) and identical to \(\bar{R}^1\) in \(Q^{1c}\). Then, there exist the two most preferred consumption bundles in \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) with respect to \(\tilde{R}^1_{\epsilon ,t(\epsilon )}\). This contradicts Lemma A3.
As for the choice of the scalars \(\bar{\epsilon }\) and \(\epsilon '\) satisfying (3), we follow Momi (2017, Proposition 2). We consider \(\epsilon _{R^1}\) satisfying (4) for each \(R^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) in a neighborhood of \(\bar{R}^1\). For \(\epsilon >0\), we consider the \(\epsilon\)-neighborhood of \(\bar{R}^1\), \({\mathcal{B}}_{\epsilon } (\bar{R}^1)\), and define \(\alpha (\epsilon )\) as the infimum of \(\epsilon _{R^1}\) for \(R^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\bigcap{\mathcal{B}}_\epsilon (\bar{R}^1)\): \(\alpha (\epsilon )=\inf _{ R^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\bigcap{\mathcal{B}}_\epsilon (\bar{R}^1)} \epsilon _{R^1}\). Note that \(\epsilon \mapsto \alpha (\epsilon )\) is a positive and decreasing function by the definition. On the other hand, we define \(\beta (\epsilon )\) as the supremum of the distance between \(f^1(R^1,\bar{\mathbf{R }}^{-1})\) and \(f^1(\bar{\mathbf{R }})\) for \(R^1\in{{\mathcal{R}}} (\bar{R}^1,Q^{1c})\bigcap{\mathcal{B}}_\epsilon (\bar{R}^1)\): \(\beta (\epsilon )=\sup _{ R^1\in{{\mathcal{R}}}(\bar{R}^1, Q^{1c})\bigcap{\mathcal{B}}_\epsilon (\bar{R}^1)} \parallel f^1(R^1,\bar{\mathbf{R }}^{-1}) - f^1(\bar{\mathbf{R }}) \parallel\). Note that \(\epsilon \mapsto \beta (\epsilon )\) is a positive and increasing function and \(\beta (\epsilon )\rightarrow 0\) as \(\epsilon \rightarrow 0\) because of the continuity of \(f^1(\cdot ,\bar{\mathbf{R }}^{-1})\) shown in Proposition A1. We pick a scalar \(\epsilon '\) satisfying \(\beta (\epsilon ') <\frac{1}{2}\alpha (\epsilon ')\) and define \(\bar{\epsilon }= \beta (\epsilon ')\). The existence of such a scalar \(\epsilon '\) is ensured by the properties of the functions \(\epsilon \mapsto \alpha (\epsilon )\) and \(\epsilon \mapsto \beta (\epsilon )\) mentioned above.
These are the desired scalars. If \(R^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) is in the \(\epsilon '\)-neighborhood of \(\bar{R}^1\), \({\mathcal{B}}_{\epsilon '}(\bar{R}^1)\), then in the neighborhood \(D_{\alpha (\epsilon ')}(f^1(R^1,\bar{\mathbf{R }}^{-1}))\), the option set \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) is in the lower left-hand side of the hyperplane \(f(R^1,\bar{\mathbf{R }}^{-1}) +p((R^1,\bar{\mathbf{R }}^{-1}),f)^\perp\):
As the distance between \(f^1(R^i,\bar{\mathbf{R }}^{-1})\) and \(f^1(\bar{\mathbf{R }})\) is at most \(\bar{\epsilon }\) and \(\alpha (\epsilon ')>2\bar{\epsilon }\), we have \(D_{\bar{\epsilon }} (f^1(\bar{\mathbf{R }}))\subset D_{\alpha (\epsilon ')}(f^1(R^1, \bar{\mathbf{R }}^{-1}))\). Hence, we have (3). \(\square\)
This proposition asserts the convexity of the option set in the following sense. For \(x'=f^i(R^{i\prime },\mathbf{R }^{-i})\) and \(x''=f^i(R^{i\prime \prime },\mathbf{R }^{-i})\) in \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\), \(i=1,2\), if a ray \([sx'+(1-s)x'']\) with \(s\in (0,1)\) has an intersection with \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\), then the intersection is written as \(t(sx'+(1-s)x'')\) with a scalar \(t\ge 1\) greater than or equal to one. If the intersection is given as \(t(sx'+(1-s)x'')\) with \(t<1\), then there exists \(R^i\) such that \(f^i(R^i,\bar{\mathbf{R }}^{-i})\) is arbitrarily close to the intersection because of the definition of \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\). Then, at least one of \(x'\) and \(x''\) is in the upper right-hand side of the hyperplane \(f^i(R^i,\bar{\mathbf{R }}^{-i})+ p((R^i, \bar{\mathbf{R }}^{-i}),f))^\perp\) regardless of the value of the price vector, which contradicts Proposition A2.
Next, we show that \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) is a surface of a strictly convex set; that is, the t in the previous paragraph is strictly greater than one. In other words, for any \(R^i\) in a neighborhood of \(\bar{R}^i\), \(f^i(R^i, \bar{\mathbf{R }}^{-i})\) is the unique intersection between \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) and the hyperplane \(f^i(R^i,\bar{\mathbf{R }}^{-i})+p((R^i,\bar{\mathbf{R }}^{-i}),f)^\perp\). The next proposition is a counterpart of Proposition 3 in Momi (2017).
Proposition A3
For any\(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\)in a neighborhood of\(\bar{R}^i\), \(i=1,2\), \(f^i(R^i,\bar{\mathbf{R }}^{-i})\)is the unique intersection between\(\overline{G^{i} (\bar{\mathbf{R }}^{-i})}\)and\(f^i(R^i,\bar{\mathbf{R }}^{-i}) +p((R^i,\bar{\mathbf{R }}^{-i}),f)^\perp\)in a neighborhood of\(f^i(R^i, \bar{\mathbf{R }})\).
Proof
As in the proof of Proposition A2, we only have to prove the statement of the proposition at the preference profile \(\bar{\mathbf{R }}\).
Without loss of generality, we prove the proposition for agent 1. We write \(f(\bar{\mathbf{R }})=\bar{\mathbf{x }}=(\bar{x}^1,\ldots , \bar{x}^N)\) and \(p(\bar{\mathbf{R }},f)=\bar{p}\). We have to prove that \(\bar{x}^1\) is the unique intersection between \(\overline{G^{1}(\bar{\mathbf{R }}^{-1})}\) and \(\bar{x}^1+\bar{p}^\perp\) in a neighborhood of \(\bar{x}^1\).
Contrary to the statement of the proposition, we suppose that for any scalar \(\epsilon >0\), there exists \(\tilde{x}^1_\epsilon\) in the \(\epsilon\)-neighborhood \(D_\epsilon (\bar{x}^1)\) of \(\bar{x}^1\) such that \(\tilde{x}_\epsilon ^1\) is different from \(\bar{x}^1\), and \(\tilde{x}_\epsilon ^1\) is the intersection between \(\overline{G^{1}(\bar{\mathbf{R }}^{-1})}\) and \(\bar{x}^1+\bar{p}^\perp\). We show a contradiction.
We first observe that when \(\epsilon\) is sufficiently small, the hyperplane \(\bar{x}^1+\bar{p}^\perp\) is tangent to \(\overline{G^{1}(\bar{\mathbf{R }}^{-1})}\) along the segment \({[}\bar{x}^1,\tilde{x}_\epsilon ^1]\equiv \{t\bar{x}^1+(1-t) \tilde{x}_\epsilon ^1\in R^L_+: 0\le t\le 1\}\). We pick an arbitrary consumption bundle \(x^1\in (\bar{x}^1, \tilde{x}_\epsilon ^1)\equiv \{t\bar{x}^1+(1-t)\tilde{x}_\epsilon ^1\in R^L_+:0<t<1\}\) and consider a preference \(R^1\in{{\mathcal{R}}} (\bar{R}^1,Q^{1c})\) in a neighborhood of \(\bar{R}^1\) so that the gradient vector of \(R^1\) at \(x^1\) is \(\bar{p}\). When \(\epsilon\) is sufficiently small, \(x^1\) is sufficiently close to \(\bar{x}^1\), and we can have such a preference \(R^1\) in a neighborhood of \(\bar{R}^1\). We let \(x^{1\prime }\) denote the most preferred consumption bundle in \(\overline{G^{1}(\bar{\mathbf{R }}^{-1})}\) with respect to \(R^1\) and \(p^\prime\) denote the gradient vector of \(R^1\) at \(x^{1\prime }\). As shown in Proposition A2, \(x^{1\prime }\) is in the lower left-hand side of the hyperplane \(\bar{x}^1+\bar{p}^\perp\). Therefore, \(\bar{p} x^{1\prime }\le \bar{p}\bar{x}^1=\bar{p}\tilde{x}_\epsilon ^1\), and hence \(\bar{p} x^{1\prime }\le \bar{p} x^1\). By the same reasoning, \(\bar{x}^1\) and \(\tilde{x}_\epsilon ^1\) are in the lower left-hand side of the hyperplane \(x^{1\prime }+( p^\prime )^\perp\). Therefore, \(p^\prime \bar{x}^1\le p^\prime x^{1\prime }\) and \(p^\prime \tilde{x}_\epsilon ^1\le p^\prime x^{1\prime }\), and hence \(p^\prime x^1\le \ p^\prime x^{1\prime }\). These two inequalities are satisfied for the two combinations \((\bar{p}, x^1)\) and \((p^\prime , x^{1\prime })\) of a gradient vector and a consumption bundle with the preference \(R^1\) if and only if \(\bar{p}= p^\prime\) and \(x^{1\prime }=x^1\). As our choice of \(x^1\) is arbitrary on \((\bar{x}^1,\tilde{x}_\epsilon ^1)\), this implies that \(\bar{x}^1+\bar{p}^\perp\) is tangent to \(\overline{G^{1}(\bar{\mathbf{R }}^{-1})}\) along the segment \([\bar{x}^1,\tilde{x}_\epsilon ^1]\). Hereafter, we assume that \(\epsilon\) is sufficiently small so that \(\bar{x}^1+\bar{p}^\perp\) is tangent to \(\overline{G^{1}(\bar{\mathbf{R }}^{-1})}\) along the segment \([\bar{x}^1,\tilde{x}_\epsilon ^1]\).
For each \(\epsilon\), we pick a consumption bundle \(\hat{x}_\epsilon ^1\in (\bar{x}^1,\tilde{x}_\epsilon ^1)\) and a preference \(\hat{R}_\epsilon ^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) such that the gradient vector of \(\hat{R}_\epsilon ^1\) at \(\hat{x}_\epsilon ^1\) is \(\bar{p}\) and \(\hat{R}_\epsilon ^1\) converges to \(\bar{R}^1\) as \(\epsilon \rightarrow 0\). We can have such a preference because \(\hat{x}^1_\epsilon \rightarrow \bar{x}\) as \(\epsilon \rightarrow 0\). Similarly, we let \(\tilde{R}_\epsilon ^1\in{{\mathcal{R}}} (\bar{R}^1,Q^{1c})\) be a preference such that the gradient vector of \(\tilde{R}_\epsilon ^1\) at \(\tilde{x}_\epsilon ^1\) is \(\bar{p}\) and \(\tilde{R}_\epsilon ^1\) converges to \(R^1\) as \(\epsilon \rightarrow 0\). It is clear that \(f^1(\tilde{R}_\epsilon ^1,\bar{\mathbf{R }}^{-1}) =\tilde{x}_\epsilon ^1\), \(f^1(\hat{R}_\epsilon ^1, \bar{\mathbf{R }}^{-1})=\hat{x}_\epsilon ^1\), and \(p((\tilde{R}_\epsilon ^1,\bar{\mathbf{R }}^{-1}),f) =p((\hat{R}_\epsilon ^1,\bar{\mathbf{R }}^{-1}),f)=\bar{p}\). We write \(f(\tilde{R}_\epsilon ^1,\bar{\mathbf{R }}^{-1})=\tilde{\mathbf{x }}_\epsilon =(\tilde{x}_\epsilon ^1,\ldots ,\tilde{x}_\epsilon ^N)\) and \(f(\hat{R}_\epsilon ^1,\bar{\mathbf{R }}^{-1}) =\hat{\mathbf{x }}_\epsilon =(\hat{x}_\epsilon ^1,\ldots ,\hat{x}_\epsilon ^N)\).
For agent \(i\ne 1\), the consumption bundles, \(\bar{x}^i\), \(\hat{x}_\epsilon ^i\), and \(\tilde{x}_\epsilon ^i\) are all on the same ray \([g(\bar{R}^i,\bar{p})]\) because of the same price vector \(\bar{p}\). We observe that \(\tilde{x}_\epsilon ^2\ne \bar{x}^2\). If \(\tilde{x}_\epsilon ^2=\bar{x}^2\), then, by comparing the two equations \(\tilde{x}^1_\epsilon +\tilde{x}_\epsilon ^2 +\sum _{i=3}^N\tilde{x}_\epsilon ^i=\Omega\) and \(\bar{x}^1+\bar{x}^2+\sum _{i=3}^N\bar{x}^i=\Omega\), we have \(\tilde{x}_\epsilon ^1-\bar{x}^1=\sum _{i=3}^N\bar{x}^i -\sum _{i=3}^N\tilde{x}_\epsilon ^i\). Considering the inner product with \(\bar{p}\) we have a contradiction, \(0=\bar{p}\cdot (\tilde{x}_\epsilon ^1-\bar{x}^1)=\bar{p}\cdot (\sum _{i=3}^N\bar{x}^i-\sum _{i=3}^N\tilde{x}_\epsilon ^i)\ne 0\), where the last inequality comes from the fact that \(\bar{p}\) is a positive vector and \(\sum _{i=3}^N\bar{x}^i-\sum _{i=3}^N\) is parallel to a positive vector \(g(R^3,\bar{p})\) under the equality of the consumption-direction vectors for \(i\ge 3\).
Then, \(\hat{x}_\epsilon ^2\) is between \(\bar{x}^2\) and \(\tilde{x}_\epsilon ^2\) on the same ray, and either \(\bar{x}^2< \hat{x}_\epsilon ^2< \tilde{x}_\epsilon ^2\) or \(\tilde{x}_\epsilon ^2<\hat{x}_\epsilon ^2< \bar{x}^2\) holds.
Figure 8 describes the situation in which the closure of agent 1’s option set is tangent to the hyperplane \(\bar{x}^1+\bar{p}^\perp\) along the segment \([\bar{x}^1,\tilde{x}_\epsilon ^1]\), contrary to the statement of the proposition. In the following proof, we show that agent 2’s option set is also flat and observe that such flat option sets contradict the efficiency and strategy-proofness of the social choice function.
We now show that when \(\epsilon\) is sufficiently small, \(\overline{G^2(\hat{R}^1_\epsilon ,\bar{\mathbf{R }}^{-\{1,2\}})}\) is flat in a neighborhood of \(\hat{x}_\epsilon ^2\). We suppose that it is not flat in any neighborhood of \(\hat{x}_\epsilon ^2\), as illustrated in Figure 8. We let \(\epsilon '>0\) be a scalar and let \(\check{R}_{\epsilon '}^2\in{{\mathcal{R}}}(\bar{R}^2,Q^{2c})\) be agent 2’s preference in the \(\epsilon '\) neighborhood \({\mathcal{B}}_{\epsilon '}(\bar{R}^2)\) of \(\bar{R}^2\) such that the gradient vector \(\check{p}_{\epsilon ,\epsilon '}\) of \(\check{R}_{\epsilon '}^2\) at the most preferred consumption bundle in \(\overline{G^2(\hat{R}^1_\epsilon ,\bar{\mathbf{R }}^{-\{1,2\}})}\) with respect to \(\check{R}_{\epsilon '}^2\) is different from \(\bar{p}\), as illustrated in the figure. As the closure of the option set is not flat in any neighborhood of \(\hat{x}^2_\epsilon\), we can have such a preference \(\check{R}_{\epsilon '}^2 \in{{\mathcal{R}}}(\bar{R}^2,Q^{2c})\) in any \(\epsilon '\)-neighborhood of \(\bar{R}^2\). We write \(f(\hat{R}_\epsilon ^1,\check{R}_{\epsilon '}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\check{\mathbf{x }}_{\epsilon ,\epsilon '} =(\check{x}_{\epsilon ,\epsilon '}^1,\ldots ,\check{x}_{\epsilon , \epsilon '}^N)\).Footnote 9 We have \(\check{p}_{\epsilon ,\epsilon '} \rightarrow \bar{p}\) and \((\check{x}_{\epsilon ,\epsilon '}^1, \check{x}_{\epsilon ,\epsilon '}^2)\rightarrow (\hat{x}_\epsilon ^1, \hat{x}_\epsilon ^2)\) as \(\epsilon '\rightarrow 0\).
As \(\hat{x}_\epsilon ^1\) is between \(\bar{x}^1\) and \(\tilde{x}_\epsilon ^1\), either \(\check{p}_{\epsilon ,\epsilon '} \bar{x}^1>\check{p}_{\epsilon ,\epsilon '}\hat{x}_\epsilon ^1 >\check{p}_{\epsilon ,\epsilon '}\tilde{x}_\epsilon ^1\), \(\check{p}_{\epsilon ,\epsilon '}\bar{x}^1<\check{p}_{\epsilon ,\epsilon '} \hat{x}_\epsilon ^1<\check{p}_{\epsilon ,\epsilon '}\tilde{x}_\epsilon ^1\), or \(\check{p}_{\epsilon ,\epsilon '} \bar{x}^1=\check{p}_{\epsilon , \epsilon '}\hat{x}_\epsilon ^1=\check{p}_{\epsilon ,\epsilon '}\tilde{x}_\epsilon ^1\) holds. When \(\check{p}_{\epsilon ,\epsilon '} \bar{x}^1>\check{p}_{\epsilon ,\epsilon '}\hat{x}_\epsilon ^1 >\check{p}_{\epsilon ,\epsilon '}\tilde{x}_\epsilon ^1\), as illustrated in Fig. 8, or when \(\check{p}_{\epsilon ,\epsilon '} \bar{x}^1=\check{p}_{\epsilon ,\epsilon '}\hat{x}_\epsilon ^1 =\check{p}_{\epsilon ,\epsilon '}\tilde{x}_\epsilon ^1\), we focus on the two combinations \((\bar{x}^1,\bar{p})\) and \((\check{x}_{\epsilon ,\epsilon '}^1,\check{p}_{\epsilon ,\epsilon '})\) of a consumption bundle and a price vector. We consider a preference \(R_{\epsilon ,\epsilon '}^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) in a neighborhood of \(\bar{R}^1\) such that the gradient vector of \(R_{\epsilon ,\epsilon '}^1\) at \(\bar{x}^1\) is \(\bar{p}\) and that at \(\check{x}_{\epsilon ,\epsilon '}^1\) is \(\check{p}_{\epsilon , \epsilon '}\): \(\bar{p}=p(R_{\epsilon ,\epsilon '}^1,\bar{x}^1)\) and \(\check{p}_{\epsilon ,\epsilon '}=p(R_{\epsilon ,\epsilon '}^1, \check{x}_{\epsilon ,\epsilon '}^1)\). Refer to Momi (2017) for an example of such a preference.
With the preference \(R_{\epsilon ,\epsilon '}^1\), we have \(f^2(R_{\epsilon ,\epsilon '}^1, \check{R}^2_{\epsilon , \epsilon '},\bar{\mathbf{R }}^{-\{1,2\}}) =\check{x}^2_{\epsilon , \epsilon '}\) and \(f^2(R_{\epsilon ,\epsilon '}^1, \bar{\mathbf{R }}^{-2}) =\bar{x}^2\). This contradicts the strategy-proofness of f with respect to agent 2 because \(\check{x}^2_{\epsilon ,\epsilon '}\rightarrow \hat{x}^2_\epsilon\) as \(\epsilon '\rightarrow 0\), and \(\hat{x}_\epsilon ^2\), which is on the same ray as \(\bar{x}^2\), satisfies \(\hat{x}_\epsilon ^2<\bar{x}^2\) or \(\bar{x}^2<\hat{x}_\epsilon ^2\) as mentioned above.
The discussion is symmetric when \(\check{p}_{\epsilon ,\epsilon '} \bar{x}^1<\check{p}_{\epsilon ,\epsilon '}\hat{x}_{\epsilon ,\epsilon '}^1 <\check{p}_{\epsilon ,\epsilon '}\tilde{x}_\epsilon ^1\). We focus on the two pairs \((\check{x}_{\epsilon ,\epsilon '}^1, \check{p}_{\epsilon , \epsilon '})\) and \((\tilde{x}_\epsilon ^1,\bar{p})\). Similar to the discussion above, we consider a preference \(R_{\epsilon ,\epsilon '}^1 \in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) in a neighborhood of \(\tilde{R}_\epsilon ^1\), and thus, in a neighborhood of \(\bar{R}^1\), such that the gradient vectors of \(R_{\epsilon ,\epsilon '}^1\) at \(\tilde{x}_\epsilon ^1\) and \(\check{x}_{\epsilon ,\epsilon '}^1\) are \(\bar{p}\) and \(\check{p}_{\epsilon ,\epsilon '}\), respectively. Then, we have \(f^i(R_{\epsilon ,\epsilon '}^1, \check{R}_{\epsilon , \epsilon '}^2,\bar{\mathbf{R }}^{-\{1,2\}})=\check{x}^i_{\epsilon , \epsilon '}\) for \(i=1,2\), which converges to \(\hat{x}^i_\epsilon\) as \(\epsilon '\rightarrow 0\), and \(f^i(R_{\epsilon ,\epsilon '}^1, \bar{\mathbf{R }}^{-2})=\tilde{x}^i_\epsilon\), \(i=1,2\). This again contradicts the strategy-proofness of f with respect to agent 2. This ends the proof that \(\overline{G^2(\hat{R}^1_\epsilon , \bar{\mathbf{R }}^{-\{1,2\}})}\) is flat in a neighborhood of \(\hat{x}^2_\epsilon\) when \(\epsilon\) is sufficiently small.
In addition to \(\hat{x}_\epsilon ^1\) and \(\hat{R}_\epsilon ^1\), we pick another consumption bundle \(\acute{x}_\epsilon ^1(\ne \hat{x}_\epsilon ^1)\) on \((\bar{x}^1,\tilde{x}_\epsilon ^1)\) and another preference \(\acute{R}_\epsilon ^1\in{{\mathcal{R}}} (\bar{R}^1,Q^{1c})\) for each \(\epsilon\) such that the gradient vector of \(\acute{R}_\epsilon ^1\) at \(\acute{x}_\epsilon ^1\) is \(\bar{p}\) and \(\acute{R}_\epsilon ^1\) converges to \(\bar{R}^1\) as \(\epsilon \rightarrow 0\). It is clear that \(f^1(\acute{R}_\epsilon ^1, \bar{\mathbf{R }}^{-\{1,2\}})=\acute{x}_\epsilon ^1\) and \(p((\acute{R}_\epsilon ^1,\bar{\mathbf{R }}^{-\{1,2\}}),f)=\bar{p}\). We write \(f(\acute{R}_\epsilon ^1,\bar{\mathbf{R }}^{-\{1,2\}}) =\acute{\mathbf{x }}_\epsilon =(\acute{x}_\epsilon ^1,\ldots , \acute{x}_\epsilon ^N)\). Similar to the discussion above, \(\overline{G^2 (\acute{R}_\epsilon ^1, \bar{\mathbf{R }}^{-\{1,2\}})}\) is flat in a neighborhood of \(\acute{x}_\epsilon ^2\) when \(\epsilon\) is sufficiently small. Under the difference of the consumption-direction vectors among agents 1,2, and 3, \(\acute{x}_\epsilon ^2\) is on the same ray as \(\hat{x}_\epsilon ^2\) and \(\acute{x}_\epsilon ^2\ne \hat{x}_\epsilon ^2\) because of \(\acute{x}_\epsilon ^1\ne \hat{x}_\epsilon ^1\).
Now, we exchange the roles of agents 1 and 2. The closure of the option set \(\overline{G^2(\hat{R}_\epsilon ^1, \bar{\mathbf{R }}^{-\{1,2\}})}\) is flat in a neighborhood of \(\hat{x}_\epsilon ^2\). For a sufficiently small scalar \(\epsilon ''\), we let \(\grave{R}_{\epsilon ''}^2\in{{\mathcal{R}}} (\bar{R}^2,Q^{2c})\) be agent 2’s preference in \({\mathcal{B}}_{\epsilon ''}(\bar{R}^2)\) such that \(f^2(\hat{R}_\epsilon ^1,\grave{R}_{\epsilon ''}^2, \bar{\mathbf{R }}^{-\{1,2\}})\) is on the flat part. Note that \(f^2(\hat{R}_\epsilon ^1,\grave{R}_{\epsilon ''}^2, \bar{\mathbf{R }}^{-\{1,2\}})-\hat{x}_\epsilon ^2 \notin [g(\bar{R}^3;\bar{p})]\).
We write \(f(\hat{R}^1_\epsilon ,\grave{R}^2_{\epsilon ''}, \bar{\mathbf{R }}^{-\{1,2\}})=\grave{\mathbf{x }}_{\epsilon , \epsilon ''}=(\grave{x}_{\epsilon ,\epsilon ''}^1,\ldots , \grave{x}_{\epsilon ,\epsilon ''}^N)\). Similar to the discussion above, we now have that \(\grave{x}_{\epsilon ,\epsilon ''}^1(\ne \hat{x}_\epsilon ^1)\) is on the same ray as \(\hat{x}_\epsilon ^1\) and \(\overline{G^1(\grave{R}_{\epsilon ''}^2,\bar{\mathbf{R }}^{-\{1,2\}})}\) is flat in a neighborhood of \(\grave{x}_{\epsilon ,\epsilon ''}^1\) when \(\epsilon ''\) is sufficiently small.
We write \(f(\acute{R}_{\epsilon }^1,\grave{R}_{\epsilon ''}^2, \bar{\mathbf{R }}^{-\{1,2\}})=\dot{\mathbf{x }}_{\epsilon ,\epsilon ''} =(\dot{x}_{\epsilon ,\epsilon ''}^1,\ldots ,\dot{x}_{\epsilon ,\epsilon ''}^N)\). As \(\epsilon ''\rightarrow 0\), we have \(\grave{R}_{\epsilon ''}^2\rightarrow \bar{R}^2\), and hence \((\dot{x}^1_{\epsilon ,\epsilon ''}, \dot{x}^2_{\epsilon ,\epsilon ''})\rightarrow (\acute{x}^1_{\epsilon , \epsilon ''}, \acute{x}^2_{\epsilon ,\epsilon ''})\). Therefore, when \(\epsilon ''\) is sufficiently small, \(\dot{x}_{\epsilon , \epsilon ''}^2\) is on the flat part of \(\overline{G^2 (\acute{R}_{\epsilon }^1, \bar{\mathbf{R }}^{-\{1,2\}})}\) in a neighborhood of \(\acute{x}_{\epsilon }^2\). As \(\epsilon \rightarrow 0\), both \(\hat{R}_\epsilon ^1\) and \(\acute{R}_\epsilon ^1\) converge to \(\bar{R}^1\), and hence both preferences become closer. Therefore, when \(\epsilon\) is sufficiently small, \(\dot{x}_{\epsilon , \epsilon ''}^1\) is sufficiently close to \(\grave{x}_{\epsilon , \epsilon ''}^1\) and it is in the flat part of \(\overline{G^1 (\grave{R}_{\epsilon ''}^2,\bar{\mathbf{R }}^{-\{1,2\}})}\) in a neighborhood of \(\grave{x}_{\epsilon ,\epsilon ''}^1\).
Now, we consider four allocations, namely \(\hat{\mathbf{x }}_\epsilon\), \(\acute{\mathbf{x }}_{\epsilon }\), \(\grave{\mathbf{x }}_{\epsilon ,\epsilon ''}\), and \(\dot{\mathbf{x }}_{\epsilon ,\epsilon ''}\) with sufficiently small \(\epsilon\) and \(\epsilon ''\). Clearly, these satisfy four equations: \(\sum _{i=1}^{N}\hat{x}_\epsilon ^i=\Omega\), \(\sum _{i=1}^{N} \acute{x}_{\epsilon }^i=\Omega\), \(\sum _{i=1}^{N}\grave{x}_{\epsilon , \epsilon ''}^i=\Omega\), and \(\sum _{i=1}^{N}\dot{x}_{\epsilon , \epsilon ''}^i=\Omega\). As the price vector \(\bar{p}\) is the same in all allocations and the preferences of agents \(i\ge 3\) are unchanged, we have \(\sum _{i=3}^N\acute{x}_{\epsilon }^i =a\sum _{i=3}^N\hat{x}_\epsilon ^i\), \(\sum _{i=3}^N \grave{x}_{\epsilon ,\epsilon ''}^i=b\sum _{i=3}^N\hat{x}_\epsilon ^i\), and \(\sum _{i=3}^N\dot{x}_{\epsilon ,\epsilon ''}^i=c\sum _{i=3}^N \hat{x}_\epsilon ^i\) using some scalars a, b, and c. As for agent 1, we have \(\grave{x}_{\epsilon ,\epsilon ''}^1 =t\hat{x}_\epsilon ^1\) and \(\dot{x}_{\epsilon ,\epsilon ''}^1 =t\acute{x}_{\epsilon }^1\) with a scalar t, because \(\grave{x}_{\epsilon ,\epsilon ''}^1\) and \(\hat{x}_\epsilon ^1\) are on the same ray \([g(\hat{R}_\epsilon ^1,\bar{p})]\), \(\dot{x}_{\epsilon , \epsilon ''}^1\) and \(\acute{x}_{\epsilon }^1\) are on the same ray \([g(\acute{R}_{\epsilon }^1,\bar{p})]\), and the segments \([\grave{x}_{\epsilon ,\epsilon ''}^1,\dot{x}_{\epsilon ,\epsilon ''}^1]\) and \([\hat{x}_\epsilon ^1,\acute{x}_{\epsilon }^1]\) are both perpendicular to \(\bar{p}\). Similarly, we have \(\acute{x}_{\epsilon }^2 =s \hat{x}_\epsilon ^2\) and \(\dot{x}_{\epsilon ,\epsilon ''}^2=s\grave{x}_{\epsilon ,\epsilon ''}^2\) using a scalar s for agent 2.
Thus, we have
From the first and second equations, we have:
From the third and fourth equations, we have:
From \(\grave{x}_{\epsilon ,\epsilon ''}^1\ne \hat{x}_{\epsilon }^1\) and \(\acute{x}_{\epsilon }^2\ne \hat{x}_{\epsilon }^2\), we have \(s\ne 1\) and \(t\ne 1\). Then, from (9) and (10), we have \((t(s-a)-(sb-c))\sum _{i=3}^N\hat{x}_{\epsilon }^i=(t-1)(s-1)\Omega\); that is, \(\sum _{i=3}^N\hat{x}_{\epsilon }^i\) is parallel to \(\Omega\). Then, from (5) and (6), we have that both \(\hat{x}_{\epsilon }^1+\hat{x}_{\epsilon }^2\) and \(\acute{x}_{\epsilon }^1 +s\hat{x}_{\epsilon }^2\) are parallel to \(\Omega\), and then \(\acute{x}_{\epsilon }^1=s\hat{x}_{\epsilon }^1\). This contradicts the fact that both \(\acute{x}_{\epsilon }^1\) and \(\hat{x}_{\epsilon }^1\) are on agent 1’s flat option set perpendicular to \(\bar{p}\). \(\square\)
Proof of Proposition A3
The next proposition, which is a counterpart of Proposition 4 in Momi (2017), shows that \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) is a smooth surface in the sense that at each point \(f^i(R^i,\bar{\mathbf{R }}^{-i})\), the hyperplane tangent to \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) is unique.
Proposition A4
For any\(R^i\in{{\mathcal{R}}}(\bar{R}^i,Q^{ic})\)sufficiently close to\(\bar{R}^i\), \(i=1,2\), \(f^i(R^i,\bar{\mathbf{R }}^{-i}) +p((R^i,\bar{\mathbf{R }}^{-i}), f)^\perp\)is the unique hyperplane tangent to\(\overline{G^i(\bar{\mathbf{R }}^{-i})}\)at\(f^i(R^i,\bar{\mathbf{R }}^{-i})\).
Proof
As in the proof of Proposition A2, we only have to prove the statement of the proposition at the preference profile \(\bar{\mathbf{R }}\). Without loss of generality, we prove the statement for agent 1. We write \(f(\bar{\mathbf{R }}) =\bar{\mathbf{x }}=(\bar{x}^1,\ldots ,\bar{x}^N)\) and \(\bar{p}=p(\bar{\mathbf{R }},f)\).
As shown in Proposition A2, \(\bar{x}^1+\bar{p}^\perp\) is a hyperplane tangent to \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) at \(x^1\), and \(\overline{ G^1(\bar{\mathbf{R }}^{-1})}\) is in the lower left-hand side of this hyperplane. We suppose that \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) has an edge at \(\bar{x}^1\) and that there exists another hyperplane tangent to \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) at \(\bar{x}^1\) with a normal vector \(\tilde{p}\) different from \(\bar{p}\). We show a contradiction.
As \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) is in the lower left-hand side of \(\bar{x}^1+\bar{p}^\perp\), and in the lower left-hand side of \(\bar{x}^1+\tilde{p}^\perp\), any hyperplane \(\bar{x}^1+(t\bar{p}+(1-t)\tilde{p})^\perp\), \(t\in [0,1]\), is tangent to \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) at \(\bar{x}^1\)
We let \(\epsilon >0\) be a small scalar. For each \(\epsilon\), we pick a preference \(\tilde{R}_\epsilon ^1\) in the \(\epsilon\)-neighborhood \({\mathcal{B}}_\epsilon (\bar{R}^1)\) of \(\bar{R}^1\) such that \(\tilde{R}^1_\epsilon\) is identical to \(\bar{R}^1\) outside \(Q^1\), the gradient vector of \(\tilde{R}_\epsilon ^1\) at \(\bar{x}^1\) is different from \(\bar{p}\) and \(\bar{x}^1\) is the most preferred consumption bundle in \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) with respect to \(\tilde{R}_\epsilon ^1\). The existence of such a preference should be clear from the above discussion. We let \(\tilde{p}_\epsilon\) denote the gradient vector of \(\tilde{R}_\epsilon ^1\) at \(\bar{x}^1\): \(\tilde{p}_\epsilon =p(\tilde{R}_\epsilon ^1,\bar{x}^1)\). We write \(f(\tilde{R}_\epsilon ^1, \bar{\mathbf{R }}^{-1}) =\tilde{\mathbf{x }}_\epsilon =(\tilde{x}_\epsilon ^1,\ldots ,\tilde{x}_\epsilon ^N)\). It is clear that \(\tilde{x}_\epsilon ^1=\bar{x}^1\) and \(\tilde{p}_\epsilon =p((\tilde{R}_\epsilon ^1,\bar{\mathbf{R }}^{-1}),f)\). As \(\epsilon \rightarrow 0\), \(\tilde{R}^1_\epsilon \rightarrow \bar{R}^1\), \(\tilde{p}_\epsilon \rightarrow \bar{p}\), and \((\tilde{x}_\epsilon ^1, \tilde{x}_\epsilon ^2) \rightarrow (\bar{x}^1,\bar{x}^2)\). Figure 9 describes the situation in which the closure of agent 1’s option set has an edge at \(\bar{x}^1\), contrary to the statement of the proposition. In the following proof we observe that this induces allocations that contradict the pseudo-efficiency and strategy-proofness of the social choice function f.
As \(\bar{R}^1\) and \(\tilde{R}_\epsilon ^1\) have different gradient vectors at \(\bar{x}^1\), \(P(\bar{x}^1;\tilde{R}_\epsilon ^1)\setminus UC(\bar{x}^1;\bar{R}^1)\ne \emptyset\). Then, there exists a consumption bundle y in any neighborhood of \(\bar{x}^1\) such that y is indifferent to \(\bar{x}^1\) with respect to \(\bar{R}^1\) and y is strictly preferred to \(\bar{x}^1\) with respect to \(\tilde{R}_\epsilon ^1\). We let \(\{y_n\}_{n=1}^\infty\) be a sequence of such consumption bundles converging to \(\bar{x}^1\) as \(n\rightarrow \infty\): \(y_n\in I(\bar{x}^1;\bar{R}^1)\), \(y_n\in P(\bar{x}^1;\tilde{R}_\epsilon ^1)\), and \(y_n\rightarrow \bar{x}^1\) as \(n\rightarrow \infty\). We let \(p_n'\) denote the gradient vector of \(\bar{R}^1\) at \(y_n\): \(p_n'=p(\bar{R}^1,y_n)\).
We focus on agent 2. With each sufficiently large n, we let \(x_n^{2\prime }\) be a consumption vector on \(\overline{G^2(\bar{\mathbf{R }}^{-2})}\) such that the hyperplane \(x_n^{2\prime }+p_n^{\prime \perp }\) is tangent to \(\overline{G^2(\bar{\mathbf{R }}^{-2})}\) at \(x_n^{2\prime }\). Such a consumption vector \(x_n^{2\prime }\) is obtained uniquely because \(\bar{x}^2\) is the unique intersection between \(\overline{G^2(\bar{\mathbf{R }}^{-2})}\) and \(\bar{x}^1+\bar{p}^\perp\), as shown in Proposition A3, and \(p_n^\prime \rightarrow \bar{p}\) as \(n\rightarrow \infty\). We have \(x_n^{2\prime }\rightarrow \bar{x}^2\) as \(n\rightarrow \infty\).Footnote 10
We let \(R_n^{2\prime }\) be agent 2’s preference that is identical to \(\bar{R}^2\) outside \(Q^2\) and has gradient vector \(p_n^\prime\) at \(x_n^{2\prime }\), and converges to \(\bar{R}^2\) as \(n\rightarrow \infty\). Refer to Momi (2017, Proposition 4) for an example of such a preference. We write \(f(R_n^{2\prime },\bar{\mathbf{R }}^{-2}) =\mathbf{x }_n^\prime =(x_n^{1\prime },\ldots ,x_n^{N\prime })\). Observe that \(x_n^{1\prime }\) is on the ray \([y_n]\).
For each sufficiently small \(\epsilon\), there exists a sufficiently large n, and we can have agent 2’s preference \(\hat{R}_{\epsilon ,n}^2\) identical to \(\bar{R}^2\) outside \(Q^2\) such that (i) the gradient vector of \(\hat{R}_{\epsilon ,n}^2\) at \(\tilde{x}_\epsilon ^2\) is \(\tilde{p}_\epsilon\) and (ii) the gradient vector of \(\hat{R}_{\epsilon ,n}^2\) at \(x_{n}^{2\prime }\) is \(p_{n}'\). Refer to Momi (2017, Proposition 4) for an example of such a preference.
We write \(f(\hat{R}_{\epsilon ,n}^2, \bar{\mathbf{R }}^{-2}) =\hat{\mathbf{x }}_{\epsilon ,n}=(\hat{x}_{\epsilon ,n}^1,\ldots , \hat{x}_{\epsilon ,n}^N)\) and \(f(\tilde{R}_\epsilon ^1, \hat{R}_{\epsilon ,n}^2,\bar{\mathbf{R }}^{-\{1,2\}}) =\check{\mathbf{x }}_{\epsilon ,n}=(\check{x}_{\epsilon ,n}^1, \ldots ,\check{x}_{\epsilon ,n}^N)\). We have \(\check{x}_{\epsilon ,n}^2=\tilde{x}_\epsilon ^2\) because of (i), and hence \(\check{x}^1_{\epsilon ,n}=\tilde{x}^1_\epsilon =\bar{x}^1\) by Lemma A1. On the contrary, we have \(\hat{x}_{\epsilon ,n}^2 =x_{n}^{2\prime }\) because of (ii), and hence \(\hat{x}^1_{\epsilon ,n}={x}_{n}^{1\prime }\). Note that \(\hat{x}_{\epsilon ,n}^1\) is on the ray \([y_n]\).
We first consider the case in which \(\hat{x}_{\epsilon ,n}^1\in P(\bar{x}^1; \tilde{R}_\epsilon ^1)\). If agent 1 has the preference \(\tilde{R}_\epsilon ^1\) and faces the other agents’ preferences \((\hat{R}_{\epsilon ,n}^2,\bar{\mathbf{R }}^{-\{1,2\}})\), he is better off by reporting \(\bar{R}^1\) and achieving \(\hat{x}_{\epsilon ,n}^1\) than reporting the true preference \(\tilde{R}_\epsilon ^1\) and achieving \(\check{x}_{\epsilon ,n}^1=\tilde{x}_\epsilon ^1=\bar{x}^1\). This contradicts the strategy-proofness of f.
Next, we consider the case \(\hat{x}_{\epsilon ,n}^1\notin UC(\bar{x}^1;\bar{R}^1)\). If agent 1 has the preference \(\bar{R}^1\) and faces the other agents’ preferences \((\hat{R}_{\epsilon ,n}^2, \bar{\mathbf{R }}^{-\{1,2\}})\), he is better off by reporting \(\tilde{R}_\epsilon ^1\) and achieving \(\check{x}_{\epsilon ,n}^1 =\tilde{x}_\epsilon ^1=\bar{x}^1\) than reporting his true preference \(\bar{R}^1\) and achieving \(\hat{x}_{\epsilon ,n}^1\). Again, this contradicts the strategy-proofness of f.
As \(\hat{x}_{\epsilon ,n}^1\in [y_\epsilon ']\), where \(y_{n}\in I(\bar{x}^1;\bar{R}^1)\) and \(y_{n}\in P(\bar{x}^1; \tilde{R}_\epsilon ^{1})\), only these two cases need to be considered. \(\square\)
Proof of Proposition A4
Finally we show that \(\overline{G^i(\bar{\mathbf{R }}^{-i})}\) coincides with \(G^i(\bar{\mathbf{R }}^{-i})\) and that it is an \(L-1\)-dimensional manifold in a neighborhood of \(f^i(\bar{\mathbf{R }})\in int A\), for \(i=1,2\).
Proposition A5
For\(i=1,2\), in a neighborhood of\(f^i (\bar{\mathbf{R }})\), \(G^i(\bar{\mathbf{R }}^{-i})\)coincides with\(\overline{G^i(\bar{\mathbf{R }}^{-i})}\)and it is an\(L-1\)-dimensional manifold.
Proof
Without loss of generality, we prove the proposition for agent 1. We write \(f(\bar{\mathbf{R }})=\bar{\mathbf{x }}=(\bar{x}^1,\ldots , \bar{x}^N)\) and \(p(\bar{\mathbf{R }},f)=\bar{p}\).
We consider the Cobb–Douglas utility functions \(u^{\alpha }(x)=x_1^{\alpha _1}\cdots x_L^{\alpha _L}\) with a parameter \(\alpha =(\alpha _1,\ldots ,\alpha _L)\in S_{++}^{L-1}\) and the preferences represented by these utility functions.
Observe that the gradient vector of the preferences represented by the utility function \(u^\alpha (x)\) at a consumption bundle \(x=(x_1,\ldots ,x_L)\) is given by the normalization of \((\frac{\alpha _1}{x_1},\ldots ,\frac{\alpha _L}{x_L})\). On the contrary, if a preference represented by a Cobb–Douglas utility function \(u^\alpha (x)\) has the gradient vector \(p=(p_1,\ldots ,p_L)\) at \(x=(x_1,\ldots ,x_L)\), then the parameter \(\alpha\) is the normalization of \(({p_1}{x_1},\ldots ,{p_L}{x_L})\).
We let \(u^{\alpha ^{*}}(x)\) be the Cobb–Douglas utility function such that agent 1’s preference \(R^{1\alpha ^{*}}\) represented by \(u^{\alpha ^{*}}(x)\) has the gradient vector \(\bar{p}\) at \(\bar{x}^1\).
We consider a preference \(R^{1\alpha }\) represented by a Cobb–Douglas utility function \(u^\alpha\) where \(\alpha\) is in a neighborhood of \(\alpha ^{*}\). Then, \(R^{1\alpha }\) is in a neighborhood of \(R^{1\alpha ^{*}}\).
As f is supposed to satisfy efficiency and strategy-proofness only on \({{\mathcal{R}}}(\bar{R}^1,Q^{1c})\times{{\mathcal{R}}} (\bar{R}^2,Q^{2c})\times \{\bar{R}^3\}\times \cdots \times \{\bar{R}^N\}\), we let \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\) denote the most preferred consumption bundle in \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\) with respect to the preference \(R^{1\alpha }\). If \(R^{1\alpha }\in{{\mathcal{R}}} (\bar{R}^1,Q^{1c})\), then, \(f^1(R^{1\alpha },\bar{\mathbf{R }}^{-1}) =\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\).
We have \(\tilde{f}^1(R^{1\alpha ^{*}},\bar{\mathbf{R }}^{-i}) =\bar{x}^1\) and \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-i})\) is in a neighborhood of \(\bar{x}^1\) when \(\alpha\) is in a neighborhood of \(\alpha ^{*}\) because of the properties of \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) shown in Propositions A2–A4. Observe that \(\alpha \ne \alpha ^\prime\) implies that \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\ne \tilde{f}^1(R^{1 \alpha ^\prime },\bar{\mathbf{R }}^{-1})\) because \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1}) =\tilde{f}^1(R^{1\alpha ^\prime },\bar{\mathbf{R }}^{-1})\) and \(\alpha \ne \alpha ^\prime\) imply that \(R^{1\alpha }\) and \(R^{1\alpha ^\prime }\) have different gradient vectors at the same consumption bundle, which contradicts Proposition A4. Thus, each \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\) in a neighborhood of \(\bar{x}^1\) is identified with the corresponding parameter \(\alpha \in S_{++}^{L-1}\) in a neighborhood of \(\alpha ^{*}\), and hence in a neighborhood of \(\bar{x}^1\), \(\bigcup _{\alpha } \tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\) is an \(L-1\)-dimensional manifold.
To end the proof, we prove that in a neighborhood of \(\bar{x}^1\), \(\bigcup _{\alpha }\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\), \(G^1(\bar{\mathbf{R }}^{-1})\), and \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\) coincide. We let \(\tilde{p}_\alpha\) denote the gradient vector of \(R^{1\alpha }\) at \(\tilde{f}^1(R^{1\alpha }, \bar{\mathbf{R }}^{-1})\): \(\tilde{p}_\alpha =p(R^{1\alpha }, \tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1}))\). When \(\alpha\) is in a neighborhood of \(\alpha ^{*}\) and \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\) is in a neighborhood of \(\bar{x}^1\), we can construct a new preference \(\tilde{R}^1\in{{\mathcal{R}}}(\bar{R}^1,Q^{1c})\) such that the gradient vector of \(\tilde{R}^1\) at \(\tilde{f}^1(R^{1\alpha }, \bar{\mathbf{R }}^{-1})\) is \(\tilde{p}_\alpha\). Refer to Momi (2017, Proposition 5) for an example of such a preference.
Then, \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\) is the most preferred consumption bundle in \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\) with respect to \(\tilde{R}^1\), and \(\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1}) =f(\tilde{R}^1,\bar{\mathbf{R }}^{-1}) \in G^1(\bar{\mathbf{R }}^{-1})\), as in Lemma A2. Therefore, we have \(\bigcup _\alpha \tilde{f}(R^{1\alpha },\bar{\mathbf{R }}^{-1}) \subset G^1(\bar{\mathbf{R }}^{-1}) \subset \overline{G^1 (\bar{\mathbf{R }}^{-1})}\) in a neighborhood of \(\bar{x}^1\). To observe that any element of \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) in a neighborhood of \(\bar{x}^1\) is included in \(\bigcup _{\alpha }\tilde{f}^1(R^{1\alpha },\bar{\mathbf{R }}^{-1})\), note that any ray [y] in a neighborhood of \([\bar{x}^1]\) intersects with \(\overline{G^1(\bar{\mathbf{R }}^{-1})}\) once at most because of strategy-proofness, and hence \(\overline{G^1 (\bar{\mathbf{R }}^{-1})}\) is at most \(L-1\) dimensional. \(\square\)
Rights and permissions
About this article
Cite this article
Momi, T. Efficient and strategy-proof allocation mechanisms in many-agent economies. Soc Choice Welf 55, 325–367 (2020). https://doi.org/10.1007/s00355-020-01248-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-020-01248-0