Adaptive physics based tetrahedral mesh generation using level sets

Abstract

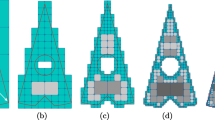
We present a tetrahedral mesh generation algorithm designed for the Lagrangian simulation of deformable bodies. The algorithm’s input is a level set (i.e., a signed distance function on a Cartesian grid or octree). First a bounding box of the object is covered with a uniform lattice of subdivision-invariant tetrahedra. The level set is then used to guide a red green adaptive subdivision procedure that is based on both the local curvature and the proximity to the object boundary. The final topology is carefully chosen so that the connectivity is suitable for large deformation and the mesh approximates the desired shape. Finally, this candidate mesh is compressed to match the object boundary. To maintain element quality during this compression phase we relax the positions of the nodes using finite elements, masses and springs, or an optimization procedure. The resulting mesh is well suited for simulation since it is highly structured, has topology chosen specifically for large deformations, and is readily refined if required during subsequent simulation. We then use this algorithm to generate meshes for the simulation of skeletal muscle from level set representations of the anatomy. The geometric complexity of biological materials makes it very difficult to generate these models procedurally and as a result we obtain most if not all data from an actual human subject. Our current method involves using voxelized data from the Visible Male [1] to create level set representations of muscle and bone geometries. Given this representation, we use simple level set operations to rebuild and repair errors in the segmented data as well as to smooth aliasing inherent in the voxelized data.

Appendix

Consider the tetrahedron defined by the points x ₁,x ₂,x ₃,x ₄ and the altitude spring from x ₄ to the triangle x ₁,x ₂,x ₃. The Cauchy stress in the tetrahedron due to this spring is

$$ \sigma _{alt} = \frac{{3f}} {{A_4 }}n_4 n_4^T , $$

where f is the scalar force in an altitude spring (see Sect. 6), A ₄ is the area of the triangle x ₁,x ₂,x ₃ and n ₄ is the outward pointing normal of the tetrahedron on face x ₁,x ₂,x ₃.

This can be shown by considering the results of [75]. A finite volume interpretation of the constant strain tetrahedron finite element forces shows that the nodal force response to an internal Cauchy stress σ can be written as

$$ f_i = \sigma \left( {\frac{{A_j n_j + A_k n_k + A_l n_l }} {3}} \right). $$

Using this result, the force on x ₄ due to σ _alt is

$$ f_4 = fn_4 \left( {\frac{{A_1 n_4^T n_1 }} {{A_4 }} + \frac{{A_2 n_4^T n_2 }} {{A_4 }} + \frac{{A_3 n_4^T n_3 }} {{A_4 }}} \right). $$

A simple geometric argument shows that −(A ₁ n ^T₄ n ₁)/A ₄ is the ratio of the projected area of the face x ₂,x ₃,x ₄ on the plane through x ₁,x ₂,x ₃ with A ₄. This is the barycentric weight of x ₄ in the plane x ₁,x ₂,x ₃ on the point x ₁. Defining the barycentric weight as w ₁, we can similarly derive

$$ \frac{{A_2 n_4^T n_2 }} {{A_4 }} = - w_2 ,\;\frac{{A_3 n_4^T n_3 }} {{A_4 }} = - w_3 . $$

Therefore, the force on x ₄ is

$$f_{4}=fn_{4}(-w_{1}-w_{2}-w_{3})=-fn_{4}. $$

Similarly,

$$ \begin{aligned} f_1 = & fn_4 \left( {\frac{{A_2 n_4^T n_2 }} {{A_4 }} + \frac{{A_3 n_4^T n_3 }} {{A_4 }} + \frac{{A_4 n_4^T n_4 }} {{A_4 }}} \right) = fn_4 (1 - w_2 - w_3 ) = fn_4 w_1 \\ f_2 = & fn_4 \left( {\frac{{A_1 n_4^T n_1 }} {{A_4 }} + \frac{{A_3 n_4^T n_3 }} {{A_4 }} + \frac{{A_4 n_4^T n_4 }} {{A_4 }}} \right) = fn_4 (1 - w_1 - w_3 ) = fn_4 w_2 \\ f_3 = & fn_4 \left( {\frac{{A_1 n_4^T n_1 }} {{A_4 }} + \frac{{A_2 n_4^T n_2 }} {{A_4 }} + \frac{{A_4 n_4^T n_4 }} {{A_4 }}} \right) = fn_4 (1 - w_1 - w_2 ) = fn_4 w_3 , \\ \end{aligned} $$

which are precisely the altitude spring forces.