Skip to main content

Advertisement

Springer Nature Link
Log in

A general topology-based framework for adaptive insertion of cohesive elements in finite element meshes

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

Large-scale simulation of separation phenomena in solids such as fracture, branching, and fragmentation requires a scalable data structure representation of the evolving model. Modeling of such phenomena can be successfully accomplished by means of cohesive models of fracture, which are versatile and effective tools for computational analysis. A common approach to insert cohesive elements in finite element meshes consists of adding discrete special interfaces (cohesive elements) between bulk elements. The insertion of cohesive elements along bulk element interfaces for fragmentation simulation imposes changes in the topology of the mesh. This paper presents a unified topology-based framework for supporting adaptive fragmentation simulations, being able to handle two- and three-dimensional models, with finite elements of any order. We represent the finite element model using a compact and “complete” topological data structure, which is capable of retrieving all adjacency relationships needed for the simulation. Moreover, we introduce a new topology-based algorithm that systematically classifies fractured facets (i.e., facets along which fracture has occurred). The algorithm follows a set of procedures that consistently perform all the topological changes needed to update the model. The proposed topology-based framework is general and ensures that the model representation remains always valid during fragmentation, even when very complex crack patterns are involved. The framework correctness and efficiency are illustrated by arbitrary insertion of cohesive elements in various finite element meshes of self-similar geometries, including both two- and three-dimensional models. These computational tests clearly show linear scaling in time, which is a key feature of the present data-structure representation. The effectiveness of the proposed approach is also demonstrated by dynamic fracture analysis through finite element simulations of actual engineering problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29

Similar content being viewed by others

Notes

  1. For reference, the tests were run on a dual-processor AMD Opteron 248 (2 × 2,193.78 MHz, 64 bits, and 16 Gb RAM).

References

  1. Cox BN, Gao H, Gross D, Rittel D (2005) Modern topics and challenges in dynamic fracture. J Mech Phys Solids 53:565–596

    Article  MATH  MathSciNet  Google Scholar 

  2. Camacho GT, Ortiz M (1996) Computational modeling of impact damage in brittle materials. Int J Solids Struct 33:2899–2938

    Article  MATH  Google Scholar 

  3. Anderson TL (2005) Fracture mechanics: fundamentals and applications, 3rd edn. CRC, Boca Raton, Florida

    MATH  Google Scholar 

  4. Belytschko T, Chen H, Xu J, Zi G (2003) Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment. Int J Numer Methods Eng 58:1873–1905

    Article  MATH  Google Scholar 

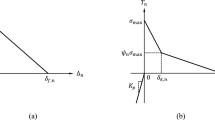
  5. Zhang Z, Paulino GH (2005) Cohesive zone modeling of dynamic failure in homogeneous and functionally graded materials. Int J Plast 21:1195–1254

    Article  MATH  Google Scholar 

  6. Zhang Z, Paulino GH, Celes W (2007) Extrinsic cohesive modeling of dynamic fracture and microbranching instability in brittle materials. Int J Numer Methods Eng (in press)

  7. Beall MW, Shephard MS (1997) A general topology-based mesh data structure. Int J Numer Methods Eng 40:1573–1596

    Article  MathSciNet  Google Scholar 

  8. Garimella RV (2002) Mesh data structure selection for mesh generation and FEA applications. Int J Numer Methods Eng 55:451–478

    Article  MATH  Google Scholar 

  9. Remacle J-F, Karamete BK, Shephard MS (2000) Algorithm oriented mesh database. In: Proceedings of the 9th international meshing roundtable, Sandia National Laboratories, pp 349–359, October

  10. Remacle J-F, Shephard MS (2003) An algorithm oriented mesh database. Int J Numer Methods Eng 58:349–374

    Article  MATH  Google Scholar 

  11. Owen SJ, Shephard MS (2003) Editorial: special issue on trends in unstructured mesh generation. Int J Numer Methods Eng 58:159–160

    Article  Google Scholar 

  12. Löhner R (1988) Some useful data structures for the generation of unstructured grids. Commun Appl Numer Methods 4:123–135

    Article  MATH  Google Scholar 

  13. Carey GF, Sharma M, Wang KC (1988) A class of data structures for 2-d and 3-d adaptive mesh refinement. Int J Numer Methods Eng 26:2607–2622

    Article  MATH  Google Scholar 

  14. Hawken DM, Townsend P, Webster MF (1992) The use of dynamic data structures in finite element applications. Int J Numer Methods Eng 33(9):1795–1811

    Article  Google Scholar 

  15. Pandolfi A, Ortiz M (1998) Solid modeling aspects of three-dimensional fragmentation. Eng Comput 14:287–308

    Article  MATH  Google Scholar 

  16. Pandolfi A, Ortiz M (2002) An efficient adaptive procedure for three-dimensional fragmentation simulations. Eng Comput 18:148–159

    Article  Google Scholar 

  17. Celes W, Paulino GH, Espinha R (2005) A compact adjacency-based topological data structure for finite element mesh representation. Int J Numer Methods Eng 64(11):1529–1565

    Article  MATH  Google Scholar 

  18. Celes W, Paulino GH, Espinha R (2005) Efficient handling of implicit entities in reduced mesh representations. J Comput Inf Sci Eng Spec Issue Mesh-Based Geometric Data Process 5(4):348–359

    Google Scholar 

  19. Klein PA, Foulk JW, Chen EP, Wimmer SA, Gao H (2001) Physics-based modeling of brittle fracture: cohesive formulations and the applications of meshfree methods. Sandia National Laboratory, Technical Report, SAND 2001-8009

  20. Ortiz M, Pandolfi A (2003) Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int J Numer Methods Eng 44:1267–1282

    Article  Google Scholar 

  21. Cirak F, Ortiz M, Pandolfi A (2005) A cohesive approach to thin-shell fracture and fragmentation. Comput Methods Appl Mech Eng 194:2604–2618

    Article  MATH  Google Scholar 

  22. Song SH, Paulino GH, Buttlar WG (2007a) A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material. Eng Fract Mech 73(18):2829–2848

    Article  Google Scholar 

  23. Song SH, Paulino GH, Buttlar WG (2007b) Simulation of crack propagation in asphalt concrete using an intrinsic cohesive zone model. ASCE J Eng Mech 132(11):1215–1223

    Article  Google Scholar 

  24. Espinosa HD, Zavattieri PD (2003) A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part 1 theory and numerical implementation. J Mater 35:333–364

    Google Scholar 

  25. Zavattieri P, Espinosa HD (2001) Grain level model analysis of crack initiation and propagation in brittle materials. Acta Mater 49:4291–4311

    Article  Google Scholar 

  26. Xu X, Needleman A (1995) Numerical simulations of dynamic crack growth along an interface. Int J Fract 74:289–324

    Article  Google Scholar 

  27. Pandolfi A, Krysl P, Ortiz M (1999) Finite element simulation of ring expansion and fragmentation: the capturing of length and time scales through cohesive models of fracture. Int J Fract 95:279–297

    Article  Google Scholar 

  28. Matous K, Geubelle PH (2006) Multiscale modelling of particle debonding in reinforced elastomers subjected to finite deformations. Int J Numer Methods Eng 65:190–223

    Article  MathSciNet  Google Scholar 

  29. Iesulauro E, Ingraffea AR, Arwade S, Wawrzynek PA (2002) Simulation of grain boundary decohesion and crack initiation in aluminum microstructure models. In: Reuter WG, Piascik RS (eds) Fatigue and fracture mechanics: 33rd volume, ASTM STP 1417. American Society for Testing and Materials, West Conshohocken, pp 715–728

  30. Weiler K (1986) Topological structures for geometric modeling, Ph.D. Thesis, Rensselaer Polytechnic Institute, New York

  31. Weiler K (1988) The radial edge structure: a topological representation for non-manifold geometric boundary modeling. In: Wozney M, McLaughlin H, Encarnacao J (eds) Geometric Modeling for CAD Applications, North-Holland, pp 3–36

  32. Mäntylä M (1988) An introduction to solid modeling. Computer Science Press, Rockville

    Google Scholar 

  33. Wawrzynek PA, Ingraffea AR (1987) Interactive finite element analysis of fracture processes: an integrated approach. Theor Appl Fract Mech 8:137–150

    Article  Google Scholar 

  34. Martha LF, Wawrzynek PA, Ingraffea AR (1993) Arbitrary crack representation using solid modeling. Eng Comput 9:63–82

    Article  Google Scholar 

  35. Paulino GH, Jin Z-H, Dodds RH Jr (2003) Failure of functionally graded materials. In: Karihaloo B, Knauss WG (eds) Comprehensive structural integrity, vol 2, Chapter 13. Elsevier Science, Amsterdam, pp 607–644

  36. Jin Z, Paulino GH, Dodds RH Jr (2003) Cohesive fracture modeling of elastic–plastic crack growth in functionally graded materials. Eng Fract Mech 70:1885–1912

    Article  Google Scholar 

  37. De Floriani L, Hui A (2003) A scalable data structure for three-dimensional non-manifold objects. In: Proceedings of the Eurographics symposium on geometry processing, Aachen, Germany, pp 72–82

  38. Kalthoff JF, Winkler S (1987) Failure mode transition at high rates of shear loading. In: Chiem CY, Kunze HD, Meyer LW (eds) Proceedings of the international conference on impact loading and dynamic behavior of materials, Bremen, Germany, pp 185–195

  39. Belytschko T, Chen H, Xu J, Zi G (2003) Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment. Int J Numer Methods Eng 58:1873–1905

    Article  MATH  Google Scholar 

  40. John R, Shah SP (1990) Mixed-mode fracture of concrete subjected to impact loading. J Struct Eng 116:585–602

    Article  Google Scholar 

  41. Ruiz G, Pandolfi A, Ortiz M (2001) Three-dimensional cohesive modeling of dynamic mixed-mode fracture. Int J Numer Methods Eng 52:97–120

    Article  Google Scholar 

Download references

Acknowledgments

Paulino gratefully acknowledges the support from NASA-Ames, Engineering for Complex Systems Program, and the NASA-Ames Chief Engineer (Dr. Tina Panontin) through grant NAG 2-1424. Both Celes and Espinha would like to thank the Tecgraf laboratory at PUC-Rio, which is mainly funded by the Brazilian oil company, Petrobras.

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, Newmark Laboratory, MC-250, 205 North Mathews Avenue, Urbana, IL, 61801-2397, USA

    Glaucio H. Paulino & Zhengyu (Jenny) Zhang

  2. Tecgraf/PUC-Rio—Computer Science Department, Pontifical Catholic University of Rio de Janeiro, Rua Marquês de São Vicente 225, Rio de Janeiro, RJ, 22450-900, Brazil

    Waldemar Celes & Rodrigo Espinha

Authors
  1. Glaucio H. Paulino
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Waldemar Celes
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rodrigo Espinha
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Zhengyu (Jenny) Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Glaucio H. Paulino.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Paulino, G.H., Celes, W., Espinha, R. et al. A general topology-based framework for adaptive insertion of cohesive elements in finite element meshes. Engineering with Computers 24, 59–78 (2008). https://doi.org/10.1007/s00366-007-0069-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-007-0069-7

Keywords