Skip to main content
Springer Nature Link
Log in

Tolerance constraint CNC tool path modeling for discretely parameterized trimmed surfaces

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

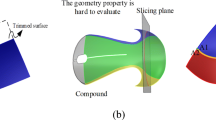
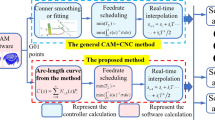
Abstract

This paper proposes a new iso-parametric tool path generation scheme for trimmed parametric surface based on two discrete parameterization techniques, namely, the Partial Differential Equation method and the newly developed “Boundary Interpolation method”. The efficiency of the scheme is measured in terms of path length and computational time for machining some typical surfaces. The side-steps and forward-steps have been formulated to suit the discrete nature of the surface representation. Conventionally the forward-step is calculated by approximating the cutting curve with osculating circle. Due to this approximation there is a possibility that the tolerance can go beyond given limit. In this paper an improved tolerance constraint method has been presented to keep the tolerance in forward-step under given value by considering the true profile of the cutting curve. Case studies show that the method presented here significantly improves the path profile by maintaining the tolerance limit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Elber G, Cohen E (1994) Toolpath generation for freeform surface models. Comput Aided Des 26(6):490–496

    Article  MATH  Google Scholar 

  2. Suresh K, Yang D (1994) Constant scallop-height machining of free-form surfaces. ASME J Eng Ind 116(2):253–259

    Article  Google Scholar 

  3. Ding S, Yang DCH, Han Z (2005) Boundary-conformed machining of turbine blades. Proc IMechE Part B J Eng Manuf 219(3):255–263

    Article  Google Scholar 

  4. George KK, Babu NR (1995) On the effective tool path planning algorithms for sculptured surface manufacture. Comput Ind Eng 28(4):823–836

    Article  Google Scholar 

  5. Huang Y, Oliver JH (1994) Non-constant parameter NC tool path generation on sculptured surfaces. Int J Adv Manuf Technol 9(5):281–290

    Article  Google Scholar 

  6. Li CL (2007) A geometric approach to boundary-conformed tool path generation. Comput Aided Des 39(11):941–952

    Article  Google Scholar 

  7. Li H, Feng HY (2002) Constant scallop-height tool path generation for three axis sculpture surface machining. Comput Aided Des 34(9):647–654

    Article  Google Scholar 

  8. Loney GC, Ozsoy TM (1987) NC machining of free form surfaces. Comput Aided Des 19(2):85–90

    Article  MATH  Google Scholar 

  9. Zhang LP, Nee AYC, Fuh JYH (2004) An efficient cutter contact curve tool path regeneration algorithm for sculptured surface machining. Proc IMechE Part B J Eng Manuf 218(4):389–402

    Article  Google Scholar 

  10. Sarkar S, Dey PP (2013) Tool path generation for algebraically parameterized surface. J Intell Manuf. doi:10.1007/s10845-013-0799-x

    Google Scholar 

  11. Lin RS, Koren Y (1996) Efficient tool-path planning for machining free-form surfaces. J Eng Ind ASME Trans 118(1):20–28

    Article  Google Scholar 

  12. Lasemi A, Xue D, Gu P (2010) Recent development in CNC machining of freeform surfaces: a state of the art review. Comput Aided Des 42(7):641–654

    Article  Google Scholar 

  13. Sarkar S, Dey PP (2012) A new boundary interpolation technique for parameterization of planar surfaces with four arbitrary boundary curves. Proc IMechE Part C J Mech Eng Sci 227(6):1280–1290

    Article  Google Scholar 

  14. Hsu K, Lee SL (1992) A numerical technique for two-dimensional grid generation with grid control at all of the boundaries. J Comput Phys 96(2):451–469

    Article  Google Scholar 

  15. Westgaard G, Nowacki H (2001) Construction of fair surfaces over irregular meshes. ASME. J Comput Inf Sci Eng 1(4):376–384

    Article  Google Scholar 

  16. Cebeci T, Shao JP, Kafyeke F, Laurendeau E (2005) Computational fluid dynamics for engineers. Horizons Publishing Inc., California

    Google Scholar 

  17. Thompson JF, Warsi ZUA, Mastin CW (1985) Numerical grid generation, foundations and applications. North Holland

  18. Hoffmann KA, Chiang ST (1989) Computational fluid dynamics for engineers. Engineering Education System, USA

    Google Scholar 

  19. Vladimir DL (2010) Grid generation methods. Springer, New York

    MATH  Google Scholar 

  20. Marsh D (2005) Applied geometry for computer graphics and CAD. Springer, London

    MATH  Google Scholar 

  21. Yamaguchi F (1988) Curves and surfaces in computer aided geometric design. Springer, London

    Book  MATH  Google Scholar 

  22. Sarkar S, Dey PP (2013) A new Iso-parametric machining algorithm for free-form surface. Proc IMechE Part E J Process Mech Eng. doi:10.1177/0954408913495191

    Google Scholar 

  23. Faux ID, Pratt MJ (1979) Computational geometry for design and manufacture. Ellis Horwood Limited, Chichester

    MATH  Google Scholar 

  24. Stoker JJ (1989) Differential geometry. Wiley-Interscience, New York

    MATH  Google Scholar 

  25. Hanta A, Grieve B (2000) Cartesian machining versus parametric machining: a comparative study. Int J Prod Res 38(13):3043–3065

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, 711103, India

    Subhajit Sarkar & Partha Pratim Dey

Authors
  1. Subhajit Sarkar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Partha Pratim Dey
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Subhajit Sarkar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sarkar, S., Dey, P.P. Tolerance constraint CNC tool path modeling for discretely parameterized trimmed surfaces. Engineering with Computers 31, 763–773 (2015). https://doi.org/10.1007/s00366-014-0388-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-014-0388-4

Keywords