Skip to main content
Springer Nature Link
Log in

Analytic and numerical solutions for axisymmetric flow with partial slip

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

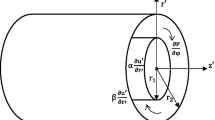
This article deals with the slip effects on the axisymmetric flow of an electrically conducting viscous fluid in the presence of a magnetic field over a non-linear radially stretching sheet. By introducing new similarity transformations, the governing partial differential equations are reduced to an ordinary differential equation. The resulting ordinary differential equation is then solved analytically using the homotopy analysis method and numerically by shooting method to show the accuracy of the analytical solution. The significant effects of various parameters on velocity field are discussed in detail. The shear stress at the wall together with some other physical parameters is tabulated and compared with existing literature, which shows an excellent agreement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Sakiadis BC (1961) Boundary layer behavior on continuous solid surface: 1. Boundary layer equations for two-dimensional and axisymmetric flow. AIChE J 7:26–28

    Article  Google Scholar 

  2. Erickson LE, Fan LT, Fox VG (1966) Heat and mass transfer on a moving continuous flat plate with suction or injection. Ind Eng Chem 5:19–25

    Google Scholar 

  3. Chen TS, Strobel FA (1980) Buoyancy effects in boundary layer adjacent to a continuous moving horizontal flat plate. J Heat Trans 102:170–172

    Article  Google Scholar 

  4. Sajid M (2009) Homotopy analysis of stretching flows with partial slip. Int J Nonlinear Sci 8:284–290

    MATH  MathSciNet  Google Scholar 

  5. Ishak A, Nazar R, Pop I (2008) Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Convers Manag 49:3265–3269

    Article  Google Scholar 

  6. Shahzad A, Ali R (2012) Approximate analytic solution of the magneto-hydrodynamic flow of non-Newtonian fluid over a vertical stretching sheet. Can J Appl Sci 2:202–215

    Google Scholar 

  7. Wang CY (2009) Analysis of viscous flow due to a stretching sheet with surface slip and suction. Nonlinear Anal: Real World Appl 10:375–380

    Article  MATH  MathSciNet  Google Scholar 

  8. Ariel PD (2007) Axisymmetric flow due to a stretching sheet with partial slip. Comput Math Appl 54:1169–1183

    Article  MATH  MathSciNet  Google Scholar 

  9. Mirgolbabaei H, Ganji DD, MEtghani M, Sobati A (2009) Adapted variational iteration method and axisymmetric flow over a stretching sheet. Wolrd J Model Simulat 5:307–314

    Google Scholar 

  10. Ariel PD (2001) Axisymmetric flow of second grade fluid past a stretching sheet. Int J Eng Sci 39:529–553

    Article  MATH  Google Scholar 

  11. Sahoo B (2010) Effects of partial slip on axisymmetric flow of an electrically conducting viscoelastic fluid past a stretching sheet. Cent Eur J Phys 8:498–508

    Google Scholar 

  12. Hayat T, Khan M, Ayub M (2004) On the explicit analytic solutions of an Oldroyd 6-constant fluid. Int J Eng Sci 42:123–135

    Article  MATH  MathSciNet  Google Scholar 

  13. Liao SJ (2005) A new branch of solutions of boundary layer flows over an impermeable stretching plate. Int J Heat Mass Transf 48:2529–2539

    Article  MATH  Google Scholar 

  14. Hayat T, Sajid M (2007) Analytic solution for axisymmetric flow and heat transfer of a second grade fluid past a stretching sheet. Int J Heat Mass Trasnf 50:75–84

    Article  MATH  MathSciNet  Google Scholar 

  15. Sajid M, Hayat T, Asghar S, Vajravelu K (2008) Analytic flow over a nonlinearly stretching sheet. Arch Appl Mech 78:127–134

    Article  MATH  Google Scholar 

  16. Sajid M, Ahmad I, Hayat T, Ayub M (2008) Series solution for unsteady axisymmetric flow and heat transfer over a radially stretching sheet. Commun Nonlinear Sci Numer Simulat 13:2193–2202

    Article  Google Scholar 

  17. Hayat T, Ahmad I, Javed T (2009) On comparison of the solutions for an axisymmetric flow. Numer Methods Partial Differ Equ 25:1204–1211

    Article  MATH  MathSciNet  Google Scholar 

  18. Khan M, Munawar S, Abbasbandy S (2010) Steady flow and heat transfer of a Sisko fluid in annular pipe. Int J Heat Mass Transf 53:1290–1297

    Article  MATH  Google Scholar 

  19. Liao SJ (2010) A short review on the homotopy analysis method in fluid mechanics. J Hydrodyn 22:882–884

    Article  Google Scholar 

  20. Faraz N, Khan Y (2011) Analytic solution of electrically conductive rotating flow of a second grade fluid over a shrinking surface. Ain Shams Eng J 2:221–226

    Article  Google Scholar 

  21. Khan M, Ali R, Shahzad A (2013) MHD Falkner–Skan flow with mixed convection and convective boundary conditions. Walailak J Sci Technol (WJST) 10(5):517–529

    Google Scholar 

  22. Shahzad A, Ali R, Khan M (2012) On the exact solution for axisymmetric flow and heat transfer over a nonlinear radially stretching sheet. Chin Phys Lett 29(8):084705

    Article  Google Scholar 

  23. Andersson HI (2002) Slip flow past a stretching surface. Acta Mech 158(1–2):121–125

    Article  MATH  Google Scholar 

  24. Bhaskar Reddy N, Poornima T, Sreenivasulu P (2014) Influence of variable thermal conductivity on MHD boundary layer slip flow of ethylene-glycol based Cu nanofluids over a stretching sheet with convective boundary condition. Int J Eng Math 2014:905158

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Angewandte Mathematik, TU Dortmund, 44227, Dortmund, Germany

    Ramzan Ali

  2. University of Central Aisa, 720001, Bishkek, Kirgizistan

    Ramzan Ali

  3. Department of Basic Sciences, UET Taxila, Taxila, Pakistan

    Azeem Shahzad

  4. Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan

    Masood Khan

  5. Department of Mathematics, COMSATS Institute of Information Technology, Abbottabad, 22060, Pakistan

    Muhammad Ayub

Authors
  1. Ramzan Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Azeem Shahzad
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Masood Khan
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Muhammad Ayub
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ramzan Ali.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, R., Shahzad, A., Khan, M. et al. Analytic and numerical solutions for axisymmetric flow with partial slip. Engineering with Computers 32, 149–154 (2016). https://doi.org/10.1007/s00366-015-0405-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-015-0405-2

Keywords