Skip to main content
Springer Nature Link
Log in

Solving fractional pantograph delay differential equations via fractional-order Boubaker polynomials

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

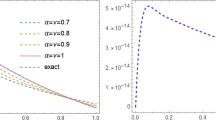
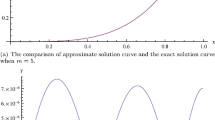
Abstract

In the current study, we introduce fractional-order Boubaker polynomials related to the Boubaker polynomials to achieve the numerical result for pantograph differential equations of fractional order in any arbitrary interval. The features of these polynomials are exploited to construct the new fractional integration and pantograph operational matrices. Then these matrices and least square approximation method are used to reorganize the problem to a nonlinear equations system which can be resolved by means of the Newton’s iterative method. The brief discussion about errors of the used estimations is deliberated and, finally, some examples are included to demonstrate the validity and applicability of our method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Rabiei K, Ordokhani Y, Babolian E (2018) Fractional-order Legendre functions and their application to solve fractional optimal control of systems described by integro-differential equations. Acta Appl Math. https://doi.org/10.1007/s10440-018-0175-0

  2. Kulish VV, Lage JL (2002) Application of fractional calculus to fluid mechanics. J Fluids Eng 124:803–806

    Article  Google Scholar 

  3. Bagley RL, Torvik PJ (1985) Fractional calculus in the transient analysis of viscoelastically damped structures. J AIAA 23:918–925

    Article  MATH  Google Scholar 

  4. Oldham KB (2010) Fractional differential equations in electrochemistry. Adv Eng Softw 41:9–12

    Article  MATH  Google Scholar 

  5. Karamali G, Dehghan M, Abbaszadeh M (2018) Numerical solution of a time-fractional PDE in the electroanalytical chemistry by a local meshless method. Eng Comput. https://doi.org/10.1007/s00366-018-0585-7

  6. Gonzalez-Parra G, Arenas AJ, Chen-Charpentier BM (2014) A fractional order epidemic model for the simulation of outbreaks of in uenza A(H1N1). Math Methods Appl Sci 37(15):2218–2226

    Article  MathSciNet  MATH  Google Scholar 

  7. Bisci GM, Radulescu VD (2015) Multiplicity results for elliptic fractional equations with subcritical term. Nonlinear Differ Equ Appl 22(4):721–739

    Article  MathSciNet  MATH  Google Scholar 

  8. Dabiri A, Butcher EA (2017) Efficient modified Chebyshev differentiation matrices for fractional differential equations. Commun Nonlinear Sci Numer Simul 50:284–310

    Article  MathSciNet  Google Scholar 

  9. Momani S, Al-Khaled K (2005) Numerical solutions for systems of fractional differential equations by the decomposition method. Appl Math Comput 162:1351–1365

    MathSciNet  MATH  Google Scholar 

  10. Saadatmandi A, Dehghan M (2010) A new operational matrix for solving fractional-order differential equations. Comput Math Appl 59:1329–1336

    MathSciNet  MATH  Google Scholar 

  11. Dehghan M, Abbaszadeh M (2017) A finite element method for the numerical solution of Rayleigh–Stokes problem for a heated generalized second grade fluid with fractional derivatives. Eng Comput 33(3):587–605

    Article  Google Scholar 

  12. Suarez L, Shokooh A (1997) An eigenvector expansion method for the solution of motion containing fractional derivatives. J Appl Mech 64:629–635

    Article  MathSciNet  MATH  Google Scholar 

  13. Bataineh AS, Alomari AK, Noorani MSM, Hashim I, Nazar R (2009) Series solutions of systems of nonlinear fractional differential equations. Acta Appl Math 105(2):189–198

    Article  MathSciNet  MATH  Google Scholar 

  14. Odibat Z, Momani S (2006) Application of variational iteration method to nonlinear differential equations of fractional order. Int J Nonlinear Sci Numer Simul 1(7):15–27

    MathSciNet  MATH  Google Scholar 

  15. Saadatmandi A, Dehghan M (2009) Variational iteration method for solving a generalized pantograph equation. Comput Math Appl 58(11):2190–2196

    Article  MathSciNet  MATH  Google Scholar 

  16. Dehghan M, Abbaszadeh M (2018) An efficient technique based on finite difference/finite element method for solution of two-dimensional space/multi-time fractional BlochTorrey equations. Appl Numer Math 131:190–206

    Article  MathSciNet  MATH  Google Scholar 

  17. Dehghan M, Abbaszadeh M (2018) A finite difference/finite element technique with error estimate for space fractional tempered diffusion-wave equation. Comput Math Appl 75(8):2903–2914

    Article  MathSciNet  MATH  Google Scholar 

  18. Dehghan M, Abbaszadeh M (2018) A Legendre spectral element method (SEM) based on the modified bases for solving neutral delay distributedorder fractional damped diffusionwave equation. Math Methods Appl Sci 41(9):3476–3494

    Article  MathSciNet  MATH  Google Scholar 

  19. Kuang Y (1993) Delay differential equations with applications in population dynamics. Academic Press, Boston

    MATH  Google Scholar 

  20. Macdoonald N (1989) Biological delay systems: linear stability theory. Cambridge University Press, Cambridge

    Google Scholar 

  21. Niculescu SI (2001) Delay effects on stability: a robust approach. Springer, Berlin

    MATH  Google Scholar 

  22. Hale JK, Verduyn Lunel SM (1993) Introduction to functional differential equations. Applied mathematical sciences, vol 99. Springer, New York

    Book  MATH  Google Scholar 

  23. Bonilla B, Rivero M, Rodriguez-Germa L, Trujillo JJ (2007) Fractional differential equations as alternative models to nonlinear differential equations. Appl Math Comput 187:79–88

    MathSciNet  MATH  Google Scholar 

  24. Magin RL (2010) Fractional calculus models of complex dynamics in biological tissues. Comput Math Appl 59:1586–1593

    Article  MathSciNet  MATH  Google Scholar 

  25. Ockendon JR, Tayler AB (1971) The dynamics of a current collection system for an electric locomotive. Proc R Soc Lond Ser A 332:447–468

    Article  Google Scholar 

  26. Dehghan M, Shakeri F (2008) The use of the decomposition procedure of Adomian for solving a delay differential equation arising in electrodynamics. Phys Scr 78:1–11

    Article  MATH  Google Scholar 

  27. Sedaghat S, Ordokhani Y, Dehghan M (2012) Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun Nonl Sci Numer Simul 17:4815–4830

    Article  MathSciNet  MATH  Google Scholar 

  28. Yu ZH (2008) Variational iteration method for solving the multi-pantograph delay equation. Phys Lett A 372:6475–6479

    Article  MathSciNet  MATH  Google Scholar 

  29. Tohidi E, Bhrawy AH, Erfani KA (2012) Collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl Math Model 37:4283–4294

    Article  MathSciNet  MATH  Google Scholar 

  30. Bahsi M, Cevik M, Sezer M (2015) Orthoexponential polynomial solutions of delay pantograph differential equations with residual error estimation. Appl Math Comput 271:11–21

    MathSciNet  MATH  Google Scholar 

  31. Guglielmi N, Zennaro M (2003) Stability of one-leg \(\varTheta\)-methods for the variable coefficient pantograph equation on the quasi-geometric mesh. IMA J Numer Anal 23:421–38

    Article  MathSciNet  MATH  Google Scholar 

  32. Saeed U, Rehman M (2014) Hermite wavelet method for fractional delay differential equations. J Differ Equ 2014:8 (Article ID 359093)

    Article  Google Scholar 

  33. Yang Y, Huang Y (2013) Spectral-collocation methods for fractional pantograph delay-integrodifferential equations. Adv Math Phys 2013:14 (Article ID 821327)

    MathSciNet  MATH  Google Scholar 

  34. Rahimkhani P, Ordokhania Y, Babolian E (2017) Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. J Comput Appl Math 309:493–510

    Article  MathSciNet  MATH  Google Scholar 

  35. Anapali A, Ozturk Y, Gulsu M (2015) Numerical approach for solving fractional pantograph equation. Int J Comput Appl 113:9

    MATH  Google Scholar 

  36. Bhrawy AH, Al-Zahrani AA, Alhamed YA, Baleanu D (2014) A new generalized Laguerre–Gauss collocation scheme for numerical solution of generalized fractional pantograph equation. Rom J Phys 59:646–657

    MATH  Google Scholar 

  37. Boubaker K (2007) On modified Boubaker polynomials: some differential and analytical properties of the new polynomial issued from an attempt for solving bi-varied heat equation. Trends Appl Sci Res 2:540–544

    Article  Google Scholar 

  38. Mahmoud BKB (2009) Temperature 3D profiling in cryogenic cylindrical devices using Boubaker polynomials expansion scheme (BPES). Cryogenics 49:217–220

    Article  Google Scholar 

  39. Dada M, Awojoyogbe OB, Boubaker K (2009) Heat transfer spray model: an improved theoretical thermal time-response to uniform layers deposit using Bessel and Boubaker polynomials. Curr Appl Phys 9:622–624

    Article  Google Scholar 

  40. Kumar AS (2010) An analytical solution to applied mathematics-related Love’s equation using the Boubaker polynomials expansion scheme. J Franklin Inst 347(9):1755–1761

    Article  MathSciNet  MATH  Google Scholar 

  41. Boubaker K (2011) Boubaker polynomials expansion scheme (BPES) solution to Boltzmann diffusion equation in the case of strongly anisotropic neutral particles forwardbackward scattering. Ann Nucl Energy 38:1715–1717

    Article  Google Scholar 

  42. Kafash A, Delavarkhalafi A, Karbassi AS, Boubaker K (2014) A numerical approach for solving optimal control problems using the Boubaker polynomials expansion scheme. J Interpolat Approx Sci Comput 2014:1–18

    MathSciNet  Google Scholar 

  43. Rabiei K, Ordokhani Y, Babolian E (2017) The Boubaker polynomials and their application to solve fractional optimal control problems. Nonlinear Dyn 88(2):1013–1026

    Article  MathSciNet  MATH  Google Scholar 

  44. Rabiei K, Ordokhani Y, Babolian E (2018) Fractional-order Boubaker functions and their applications in solving delay fractional optimal control problems. J Vib Control 24:3370. https://doi.org/10.1177/1077546317705041

    Article  MathSciNet  MATH  Google Scholar 

  45. Podlubny I (1999) Fractional diferential equations. Academic Press, New York

    MATH  Google Scholar 

  46. Kreyszig E (1978) Introductory functional analysis with applications. Wiley, New York

    MATH  Google Scholar 

  47. Bellen A, Zennaro M (2003) Numerical methods for delay differential equations. Numerical mathematics and scientific computation. The Clarendon Press, New York

    Book  MATH  Google Scholar 

  48. Wang WS, Li SF (2007) On the one-leg—method for solving nonlinear neutral functional differential equations. Appl Math Comput 193:285–301

    MathSciNet  MATH  Google Scholar 

  49. Chen X, Wang L (2010) The variational iteration method for solving a neutral functional differential equation with proportional delays. Comput Math Appl 59:2696–2702

    Article  MathSciNet  MATH  Google Scholar 

  50. Brunner H, Huang Q, Xies H (2011) Discontinuous Galerkin methods for delay differential equations of pantograph type. SIAM J Numer Anal 48:1944–1967

    Article  MathSciNet  MATH  Google Scholar 

  51. Muroya Y, Ishiwata E, Brunner H (2003) On the attainable order of collocation methods for pantograph integro-differential equations. J Comput Appl Math 152:347–366

    Article  MathSciNet  MATH  Google Scholar 

  52. Rahimkhani P, Ordokhania Y, Babolian E (2017) A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer Algorithms 74(1):223–245

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We express our appreciation to the reviewers for their helpful comments, which improved the quality of this work.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

    Kobra Rabiei & Yadollah Ordokhani

Authors
  1. Kobra Rabiei
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yadollah Ordokhani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yadollah Ordokhani.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rabiei, K., Ordokhani, Y. Solving fractional pantograph delay differential equations via fractional-order Boubaker polynomials. Engineering with Computers 35, 1431–1441 (2019). https://doi.org/10.1007/s00366-018-0673-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-018-0673-8

Keywords