Abstract
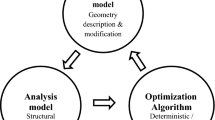
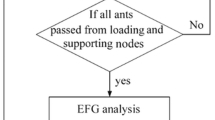
This paper puts forward a newer approach for structural shape optimization by combining a meshless method (MM), i.e. element-free Galerkin (EFG) method, with swarm intelligence (SI)-based stochastic ‘zero-order’ search technique, i.e. artificial bee colony (ABC), for 2D linear elastic problems. The proposed combination is extremely beneficial in structural shape optimization because MM, when used for structural analysis in shape optimization, eliminates inherent issues of well-known grid-based numerical techniques (i.e. FEM) such as mesh distortion and subsequent remeshing while handling large shape changes, poor accuracy due to discontinuous secondary field variables across element boundaries needing costly post-processing techniques and grid optimization to minimize computational errors. Population-based stochastic optimization technique such as ABC eliminates computational burden, complexity and errors associated with design sensitivity analysis. For design boundary representation, Akima spline interpolation has been used in the present work owing to its enhanced stability and smoothness over cubic spline. The effectiveness, validity and performance of the proposed technique are established through numerical examples of cantilever beam and fillet geometry in 2D linear elasticity for shape optimization with behavior constraints on displacement and von Mises stress. For both these problems, influence of a number of design variables in shape optimization has also been investigated.

















Similar content being viewed by others
References
Wall WA, Frenzel MA, Cyron C (2008) Isogeometric structural shape optimization. Comput Methods Appl Mech Eng 197:2976–2988
Imam MH (1982) Three-dimensional shape optimization. Int J Numer Methods Eng 18:661–673
Zienkiewicz OC, Campbell JS (1973) Shape optimization and sequential linear programming. In: Gallagher RH, Zienkiewicz OC (eds) Optimum structural design. Wiley, New York, pp 109–126
Bhavikatti SS, Ramakrishnan CV (1977) Optimum design of fillets in flat and round tension bars. Proceedings of the ASME, Design Engineering Technical Conference, Chicago, Illinois, 77-DET-45
Bhavikatti SS, Ramakrishnan CV (1980) Optimum shape design of rotating disks. Comput Struct 11:397–401
Braibant V, Fleury C (1984) Shape optimal design using B-splines. Comput Methods Appl Mech Eng 44:247–267
Annicchiarico W, Cerrolaza M (1999) Finite elements, genetic algorithms and b-splines: a combined technique for shape optimization. Finite Elements Anal Des 33:125–141
Botkin ME (1982) Shape optimization of plate and shell structures. AIAA J 20(2):268–273
Wang SY, Sun Y, Gallagher RH (1985) Sensitivity analysis in shape optimization of continuum structures. Comp Struct 20(5):855–867
Belegundu AD, Rajan SD (1988) A shape optimization approach based on natural design variables and shape functions. Comput Methods Appl Mech Eng 66:87–106
Tortorelli DA (1993) A geometric representation scheme suitable for shape optimization. Mech Struct Mach 21(1):95–121
Firl M, Wuchner R, Bletzinger KU (2013) Regularization of shape optimization problems using FE-based parametrization. Struct Multidisc Optim 47:507–521
Stavropoulou E, Hojjat M, Bletzinger KU (2014) In-plane mesh regularization for node-based shape optimization problems. Comput Methods Appl Mech Engrg 275:39–54
Haftka RT, Grandhi RV (1986) Structural shape optimization: a survey. Comput Methods Appl Mech Eng 57(1):91–106
Ding Y (1986) Shape optimization of structures: a literature survey. Comput Struct 24(6):985–1004
Mackerle J (2003) Topology and shape optimization of structures using FEM and BEM-a bibliography (1999–2001). Finite Elem Anal Des 39:243–253
Bennett JA, Botkin ME (1985) Structural shape optimization with geometric description and adaptive mesh refinement. AIAA J 23(3):458–464
Kim NH, Choi KK (2005) Structural sensitivity analysis and optimization 1: linear systems. Springer, New York
Lacroix D, Bouillard P (2003) Improved sensitivity analysis by a coupled FE-EFG method. Comput Struct 81:2431–2439
Grindeanu I, Choi KK, Chen JS, Chnag KH (1999) Shape design optimization of Hyperelastic structures using a Meshless method. AIAA J 37(8):990–997
Diaz AR, Kikuchi N, Taylor JE (1983) A method of grid optimization for finite element methods. Comp Methods Appl Mech Eng 41:29–45
Ingber MS, Mitra AK (1986) Grid optimization for the boundary element method. Int J Numer Methods Eng 23:2121–2136
Bathe KJ (1996) Finite element procedures. Prentice Hall, Englewood Cliffs
Najafi AR, Safdaric M, Tortorelli DA, Geubelle PH (2015) A gradient based shape optimization scheme using an interface-enriched generalized FEM. Comput Methods Appl Mech Eng 296:1–17
Kim NH, Chang Y (2005) Eulerian shape design sensitivity analysis and optimization with a fixed grid. Comput Methods Appl Mech Eng 194:3291–3314
Gracia MJ, Gonzalez CA (2004) Shape optimization of continuum structures via evolution strategies and fixed grid finite element analysis. Struct Multidisc Optim 26:92–98
Garcia-Ruiz MJ, Steven GP (1999) Fixed grid finite element in elasticity optimization. Eng Comput 16(2):145–164
Hughes TJR, Cottrell JA, BazilevsY (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195
Fubeder D, Simeon B, Vuong AV (2015) Fundamental aspects of shape optimization in the context of isogeometric analysis. Comput Methods Appl Mech Eng 286:313–331
Ha SH, Choi KK, Cho S (2010) Numerical method for shape optimization using T-spline based isogeometric method. Struct Multidisc Optim 42:417–428
Qian X (2010) Full analytical sensitivities in NURBS based isogeometric shape optimization. Comput Methods Appl Mech Eng 199:2059–2071
Bobaru F, Rachakonda S (2004) Boundary layer in shape optimization of convective fins using a meshless approach. Int J Numer Methods Eng 60(7):1215–1236
Belytschko TY, Lu YY, Gu L (1994) Element-free Galerkin methods. Int J Numer Methods Eng 37(2):229–256
Mota Soares CA, Radrigues HC, Choi KK (1984) Shape optimal structural design using boundary elements and minimum compliance techniques. ASME 84-DET-57
Mota Soares CA, Rodrigues HC, Oliveira Faria LM, Haug EJ (1984) Optimization of the geometry of shafts using boundary elements. ASME J Mech Trans Autom Des 106(2):199–203
Zhang J, Gong S, Huang Y, Qiu A, Chen R (2008) Structural dynamic shape optimization and sensitivity analysis based on RKPM. Struct Multidisc Optim 36:307–317
Kim NH, Choi KK, Botkin ME (2003) Numerical method for shape optimization using meshless method. Struct Multidisc Optim 24:418–429
Bobaru F, Mukherjee S (2001) Shape sensitivity analysis and shape optimization in planar using the element-free Galerkin method. Comput Methods Appl Mech Eng 190:4319–4937
Phan AV, Mukherjee S, Mayer JRR (1998) Stresses, stress sensitivities and shape optimization in two-dimensional linear elasticity by the boundary contour method. Int J Numer Methods Eng 42:1391:1407
Zhao Z (1991) In shape design sensitivity analysis and optimization using the boundary element method. Springer, New York
Bobaru F, Mukherjee S (2002) Meshless approach to shape optimization of linear thermoelastic solids. Int J Numer Methods Eng 53:765–796
Hou JW, Sheen JS, Chuang CH (1992) Shape-sensitivity analysis and design optimization of linear, thermoelastic solids. AIAA J 30(2):528–537
Bobaru F, Rachakonda S (2004) Optimal shape profiles for cooling fins of high and low conductivity. Int J Heat Mass Transf 47(23):4953–4966
Bobaru F, Rachakonda S (2006) E(FG)2: a new fixed-grid shape optimization method based on the element-free Galerkin mesh-free analysis: taking large steps in shape optimization. Struct Multidiscip Optim 32:215–228
Zou W, Zhou JX, Zhang ZQ, Li Q (2007) A truly meshless method based on partition of unity quadrature for shape optimization of continua. Comput Mech 39:357–365
Zhang ZQ, Zhou JX, Zhou N, Wang XM, Zhang L (2005) Shape optimization using reproducing kernel particle method and an enriched genetic algorithm. Comput Methods Appl Mech Eng 194:4048–4070
Banichuk NV, Serra M, Sinitsyn A (2006) Shape optimization of quasi-brittle axisymmetric shells by genetic algorithm. Comput Struct 84:1925–1933
Muc A, Gurba W (2001) Genetic algorithms and finite element analysis in optimization of composite structures. Compos Struct 54:275–281
Sonmez FO (2007) Shape optimization of 2D structures using simulated annealing. Comput Methods Appl Mech Eng 196:3279–3299
Shim PY, Manoochehri S (1997) Generating optimal configurations in structural design using simulated annealing. Int J Numer methods Eng 40:1053–1069
Karaboga D (2005) An Idea Based on Honey Bee Swarm for Numerical Optimization. Technical Report-TR06, Erciyes University
Karaboga D, Akay B (2009) A comparative study of Artificial Bee Colony algorithm. Appl Math Comput 214:108–132
Sonmez M (2011) Discrete optimum design of truss structures using artificial bee colony algorithm. Struct Multidisc Optim 43:85–97
Park JY, Han SY (2013) Application of artificial bee colony algorithm to topology optimization for dynamic stiffness problems. Comput Math Appl 66:1879–1891
Zhu T, Atlure SN (1998) A modified collocation method and a penalty formulation for enforcing the essential boundary conditions in the element free Galerkin method. Comput Mech 21:211–222
Lu YY, Belytschko T, Gu L (1994) A new implementation of the element free Galerkin method. Comput Methods Appl Mech Eng 113(3–4):397–414
Krongauz Y, Belytschko T (1996) Enforcement of essential boundary conditions in meshless approximations using finite elements. Comput Methods Appl Mech Eng 131(1–2):133–145
Beissel S, Belytschko T (1996) Nodal integration of the element-free Galerkin method. Comput Methods Appl Mech Eng 139:49–71
Chen JS, Wu CT, Yoon S, You Y (2001) A stabilized conforming nodal integration for Galerkin mesh-free methods. Int J Numer Methods Eng 50:435–466
Carpinteri A, Ferro G, Ventura G (2002) The partition of unity quadrature in meshless methods. Int J Numer Methods Eng 54:987
DuflotM HungND (2002) A truly meshless Galerkin method based on a moving least squares quadrature. Commun Numer Methods Eng 18:441–449
Zuohiui P (2000) Treatment of point loads in element free Galerkin method (EFGM). Commun Numer Meth Engrg 16:335–341
Karaboga D, Gorkemli B, Ozturk C, Karaboga N (2012) A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artf Intell Rev 42:21–57
Karaboga D, Basturk B (2007) On the performance of artificial bee colony (ABC) algorithm. Appl Soft Comput 8:687–697
Tereshko V (2000) Reaction-diffusion model of a honeybee colony’s foraging behaviour. In: Schoenauer M et al (eds) Parallel problem solving from nature VI. Lecture Notes in Computer Science, vol 1917. Springer, Berlin, pp 807–816
Jordehi AR (2014) A review on constraint handling strategies in particle swarm optimization. Neural Comput Appl 26:1265–1275
Akima H (1970) A new method of interpolation and smooth curve fitting based on local procedures. J Assoc Comput Mach 17(4):589–602
Wang C, Yu T, Shao G, Nguyen TT, Bui TQ (2018) Shape optimization of structures with cutouts by an efficient approach based on XIGA and chaotic particle swarm optimization. Eur J Mech A Solids 74:176–187
Lian H, Kerfriden P, Bordas SPA (2016) Implementation of regularized isogeometric boundary element methods for gradient-based shape optimization in two-dimensional linear elasticity. Int J Numer Meth Eng 106:972–1017
Sun SH, Yu TT, Nguyen TT, Atroshchenko E, Bui TQ (2018) Structural shape optimization by IGABEM and particle swarm optimization algorithm. Eng Anal Bound Elem 88:26–40
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Daxini, S.D., Prajapati, J.M. Numerical shape optimization based on meshless method and stochastic optimization technique. Engineering with Computers 36, 565–586 (2020). https://doi.org/10.1007/s00366-019-00714-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-019-00714-3