Abstract
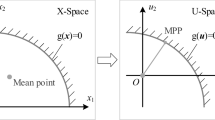
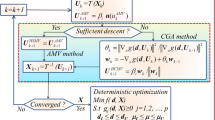
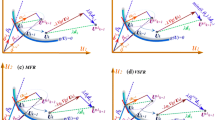
The performances of first-order reliability method (FORM) are highly important owing to its accuracy and efficiency in the structural reliability analysis. In the gradient methods-based sensitivity analysis, the iterative formula of FORM is established using the gradient vector which it may not compute for some structural problems with discrete or non-continuous performance functions. In this study, the probabilistic Gaussian global-best harmony search (GGHS) optimization is implemented to search for the most probable point in the structural reliability analysis. The proposed GGHS approach for reliability analyses is performed based on two main adjusted processes using the random Gaussian generation. The accuracy and efficiency of the GGHS are compared with original harmony search (HS) algorithm and three modified versions of HS as improved HS, global-best HS, and improved global-best HS based on a mathematical and three structural problems. The obtained results illustrated that the PGGHS is more efficient than other modified versions of HS and provides the accurate results for discrete performance functions compared to original FORM-based gradient method.









Similar content being viewed by others
References
Jiang C, Qiu H, Li X, Chen Z, Gao L, Li P (2019) Iterative reliable design space approach for efficient reliability-based design optimization. Eng Comput. https://doi.org/10.1007/s00366-018-00691-z
Meng Z, Pu Y, Zhou H (2018) Adaptive stability transformation method of chaos control for first order reliability method. Eng Comput 34(4):671–683. https://doi.org/10.1007/s00366-017-0566-2
Keshtegar B (2017) A modified mean value of performance measure approach for reliability-based design optimization. Arab J Sci Eng 42(3):1093–1101
Keshtegar B, Chakraborty S (2018) A hybrid self-adaptive conjugate first order reliability method for robust structural reliability analysis. Appl Math Model 53:319–332
Jiang C, Qiu H, Yang Z, Chen L, Gao L, Li P (2019) A general failure-pursuing sampling framework for surrogate-based reliability analysis. Reliab Eng Syst Saf 183:47–59
Zhu S-P, Liu Q, Peng W, Zhang X-C (2018) Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int J Mech Sci 142:502–517
Ditlevsen O, Madsen HO (1996) Structural reliability methods, vol 178. Wiley, New York
Yaseen ZM, Keshtegar B (2018) Limited descent-based mean value method for inverse reliability analysis. Eng Comput. https://doi.org/10.1007/s00366-018-0661-z
Keshtegar B, Kisi O (2018) RM5Tree: radial basis M5 model tree for accurate structural reliability analysis. Reliab Eng Syst Saf 180:49–61
Seghier El Amine Ben, Keshtegar MB, Correia JAFO, Lesiuk G, De Jesus AMP (2019) Reliability analysis based on hybrid algorithm of M5 model tree and Monte Carlo simulation for corroded pipelines: case of study X60 Steel grade pipes. Eng Fail Anal 97:793–803. https://doi.org/10.1016/j.engfailanal.2019.01.061
Au S-K, Beck JL (2001) Estimation of small failure probabilities in high dimensions by subset simulation. Probab Eng Mech 16(4):263–277
Hamzehkolaei NS, Miri M, Rashki M (2018) New simulation-based frameworks for multi-objective reliability-based design optimization of structures. Appl Math Model 62:1–20. https://doi.org/10.1016/j.apm.2018.05.015
Rashki M, Miri M, Moghaddam MA (2014) A simulation-based method for reliability based design optimization problems with highly nonlinear constraints. Autom Constr 47:24–36
Engelund S, Rackwitz R (1993) A benchmark study on importance sampling techniques in structural reliability. Struct Saf 12(4):255–276
Dey A, Mahadevan S (1998) Ductile structural system reliability analysis using adaptive importance sampling. Struct Saf 20(2):137–154
Nie J, Ellingwood BR (2000) Directional methods for structural reliability analysis. Struct Saf 22(3):233–249
Zhao Y-G, Ang AH (2003) System reliability assessment by method of moments. J Struct Eng 129(10):1341–1349
Zhao Y-G, Ono T (2004) On the problems of the fourth moment method. Struct Saf 26(3):343–347
Goswami S, Ghosh S, Chakraborty S (2016) Reliability analysis of structures by iterative improved response surface method. Struct Saf 60(Supplement C):56–66. https://doi.org/10.1016/j.strusafe.2016.02.002
Meng Z, Li G, Yang D, Zhan L (2017) A new directional stability transformation method of chaos control for first order reliability analysis. Struct Multidiscip Optim 55(2):601–612
Keshtegar B, Meng Z (2017) A hybrid relaxed first-order reliability method for efficient structural reliability analysis. Struct Saf 66:84–93
Roudak MA, Shayanfar MA, Barkhordari MA, Karamloo M (2017) A robust approximation method for nonlinear cases of structural reliability analysis. Int J Mech Sci 133(Supplement C):11–20. https://doi.org/10.1016/j.ijmecsci.2017.08.038
Green DK (2017) Efficient Markov Chain Monte Carlo for combined subset simulation and nonlinear finite element analysis. Comput Methods Appl Mech Eng 313:337–361
Arab HG, Ghasemi MR (2015) A fast and robust method for estimating the failure probability of structures. Proc Inst Civil Eng Struct Build 168(4):298–309
Keshtegar B, Kisi O (2017) M5 model tree and Monte Carlo simulation for efficient structural reliability analysis. Appl Math Model 48:899–910
Ghohani Arab H, Rashki M, Rostamian M, Ghavidel A, Shahraki H, Keshtegar B (2018) Refined first-order reliability method using cross-entropy optimization method. Eng Comput. https://doi.org/10.1007/s00366-018-0680-9
Li D-Q, Yang Z-Y, Cao Z-J, Au S-K, Phoon K-K (2017) System reliability analysis of slope stability using generalized subset simulation. Appl Math Model 46:650–664
Rashki M, Miri M, Moghaddam MA (2012) A new efficient simulation method to approximate the probability of failure and most probable point. Struct Saf 39:22–29
Huang J, Griffiths D (2011) Observations on FORM in a simple geomechanics example. Struct Saf 33(1):115–119
Huang X, Li Y, Zhang Y, Zhang X (2018) A new direct second-order reliability analysis method. Appl Math Model. https://doi.org/10.1016/j.apm.2017.10.026
Jian W, Zhili S, Qiang Y, Rui L (2017) Two accuracy measures of the Kriging model for structural reliability analysis. Reliab Eng Syst Saf 167(Supplement C):494–505. https://doi.org/10.1016/j.ress.2017.06.028
Zhang Z, Jiang C, Wang G, Han X (2015) First and second order approximate reliability analysis methods using evidence theory. Reliab Eng Syst Saf 137:40–49
Keshtegar B, Lee I (2016) Relaxed performance measure approach for reliability-based design optimization. Struct Multidiscip Optim 54(6):1439–1454
Keshtegar B, Chakraborty S (2018) Dynamical accelerated performance measure approach for efficient reliability-based design optimization with highly nonlinear probabilistic constraints. Reliab Eng Syst Saf 178:69–83. https://doi.org/10.1016/j.ress.2018.05.015
Keshtegar B, Hao P (2017) A hybrid self-adjusted mean value method for reliability-based design optimization using sufficient descent condition. Appl Math Model 41:257–270
Meng Z, Keshtegar B (2019) Adaptive conjugate single-loop method for efficient reliability-based design and topology optimization. Comput Methods Appl Mech Eng 344:95–119. https://doi.org/10.1016/j.cma.2018.10.009
Keshtegar B (2018) Enriched FR conjugate search directions for robust and efficient structural reliability analysis. Eng Comput 34(1):117–128
Keshtegar B, Bagheri M (2018) Fuzzy relaxed-finite step size method to enhance the instability of the fuzzy first-order reliability method using conjugate discrete map. Nonlinear Dyn 91(3):1443–1459
Keshtegar B, Baharom S, El-Shafie A (2018) Self-adaptive conjugate method for a robust and efficient performance measure approach for reliability-based design optimization. Eng Comput 34(1):187–202
Keshtegar B (2017) A hybrid conjugate finite-step length method for robust and efficient reliability analysis. Appl Math Model 45:226–237. https://doi.org/10.1016/j.apm.2016.12.027
Keshtegar B (2018) Conjugate finite-step length method for efficient and robust structural reliability analysis. Struct Eng Mech 65:415–422. https://doi.org/10.12989/sem.2018.65.4.415
Meng Z, Zhang D, Li G, Yu B (2019) An importance learning method for non-probabilistic reliability analysis and optimization. Struct Multidiscip Optim 59(4):1255–1271
Meng Z, Li G, Wang BP, Hao P (2015) A hybrid chaos control approach of the performance measure functions for reliability-based design optimization. Comput Struct 146:32–43. https://doi.org/10.1016/j.compstruc.2014.08.011
Meng Z, Yang D, Zhou H, Wang BP (2018) Convergence control of single loop approach for reliability-based design optimization. Struct Multidiscip Optim 57(3):1079–1091
Meng Z, Zhang D, Liu Z, Li G (2018) An adaptive directional boundary sampling method for efficient reliability-based design optimization. J Mech Des 140(12):121406
Keshtegar B, Hao P, Meng Z (2017) A self-adaptive modified chaos control method for reliability-based design optimization. Struct Multidiscip Optim 55(1):63–75
Keshtegar B, Hao P (2018) A hybrid descent mean value for accurate and efficient performance measure approach of reliability-based design optimization. Comput Methods Appl Mech Eng 336:237–259
Seghier El Amine Ben, Keshtegar MB, Elahmoune B (2018) Reliability analysis of low, mid and high-grade strength corroded pipes based on plastic flow theory using adaptive nonlinear conjugate map. Eng Fail Anal 90:245–261. https://doi.org/10.1016/j.engfailanal.2018.03.029
Gong J-X, Yi P (2011) A robust iterative algorithm for structural reliability analysis. Struct Multidiscip Optim 43(4):519–527
António CC (2001) A hierarchical genetic algorithm for reliability based design of geometrically non-linear composite structures. Compos Struct 54(1):37–47
Breitung K (2015) 40 years FORM: some new aspects? Probab Eng Mech 42:71–77
J-x Gong, Yi P, Zhao N (2014) Non-gradient–based algorithm for structural reliability analysis. J Eng Mech 140(6):04014029
Elegbede C (2005) Structural reliability assessment based on particles swarm optimization. Struct Saf 27(2):171–186
Santosh T, Saraf R, Ghosh A, Kushwaha H (2006) Optimum step length selection rule in modified HL–RF method for structural reliability. Int J Press Vessels Pip 83(10):742–748
Geem ZW, Kim JH, Loganathan GV (2001) A new heuristic optimization algorithm: harmony search. Simulation 76(2):60–68
Geem ZW, Choi J-Y (2007) Music composition using harmony search algorithm. In: workshops on applications of evolutionary computation, Springer, pp 593–600
Mahdavi M, Fesanghary M, Damangir E (2007) An improved harmony search algorithm for solving optimization problems. Appl Math Comput 188(2):1567–1579
Wang C-M, Huang Y-F (2010) Self-adaptive harmony search algorithm for optimization. Expert Syst Appl 37(4):2826–2837
Omran MG, Mahdavi M (2008) Global-best harmony search. Appl Math Comput 198(2):643–656
Zou D, Gao L, Wu J, Li S, Li Y (2010) A novel global harmony search algorithm for reliability problems. Comput Ind Eng 58(2):307–316
Zou D, Gao L, Wu J, Li S (2010) Novel global harmony search algorithm for unconstrained problems. Neurocomputing 73(16–18):3308–3318
El-Abd M (2013) An improved global-best harmony search algorithm. Appl Math Comput 222:94–106
Keshtegar B, Hao P, Wang Y, Li Y (2017) Optimum design of aircraft panels based on adaptive dynamic harmony search. Thin Walled Struct 118:37–45
Keshtegar B, Ozbakkaloglu T, Gholampour A (2017) Modeling the behavior of FRP-confined concrete using dynamic harmony search algorithm. Eng Comput 33(3):415–430
Yang D (2010) Chaos control for numerical instability of first order reliability method. Commun Nonlinear Sci Numer Simul 15(10):3131–3141
White DW, Jeong WY, Toğay O (2016) Comprehensive stability design of planar steel members and framing systems via inelastic buckling analysis. Int J Steel Struct 16(4):1029–1042
Zhang L, Lu Z, Wang P (2015) Efficient structural reliability analysis method based on advanced Kriging model. Appl Math Model 39(2):781–793
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest to any part for publishing this research.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations
Rights and permissions
About this article
Cite this article
Yaseen, Z.M., Aldlemy, M.S. & Oukati Sadegh, M. Non-gradient probabilistic Gaussian global-best harmony search optimization for first-order reliability method. Engineering with Computers 36, 1189–1200 (2020). https://doi.org/10.1007/s00366-019-00756-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-019-00756-7