Skip to main content
Springer Nature Link
Log in

Legendre wavelet-based iterative schemes for fourth-order elliptic equations with nonlocal boundary conditions

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

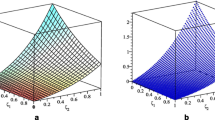
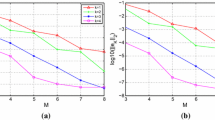
Abstract

In the literature of wavelets, there is limited report of work done to solve nonlinear differential equations with nonlocal boundary conditions. This work is a new attempt to solve a fourth-order elliptic equation with the use of nonlocal boundary conditions by coupling quasilinearization with Legendre wavelet. Since the previously available approach failed to produce reliable accuracy for certain class of problems, this iterative scheme has been suitably modified to deal with a broader class to obtain an accuracy that is reliable. To show the efficiency of the proposed numerical method, a comparison was performed with some existing methods available in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Adibi H, Assari P (2011) On the numerical solution of weakly singular Fredholm integral equations of the second kind using Legendre wavelets. J Vib Control 17(5):689–698

    Article  MathSciNet  Google Scholar 

  2. Avaji M, Dehcheshmeh SS, Hafshejani JS, Ghahfarokhi DF (2013) On the solution of linear and nonlinear fractional integro-differential equations in nano-transistors. J Comput Theor Nanosci 10:510–513

    Article  Google Scholar 

  3. Aziz I, Islam S, Nisar M (2016) An efficient numerical algorithm based on Haar wavelet for solving a class of linear and nonlinear nonlocal boundary-value problems. Calcolo 53:621–633

    Article  MathSciNet  Google Scholar 

  4. Aziz I, Islam S (2015) An efficient modified Haar wavelet collocation method for numerical solution of two-dimensional elliptic PDEs. Differ Equ Dyn Syst 9:e1003654. https://doi.org/10.1007/s12591-015-0262-x

    Article  Google Scholar 

  5. Aziz I, Islam S, Sarler B (2013) Wavelets collocation methods for the numerical solution of elliptic BV problems. Appl Math Model 37:676–694

    Article  MathSciNet  Google Scholar 

  6. Bai Z, Wang H (2002) On positive solutions of some nonlinear fourth-order beam equations. J Math Anal Appl 270:357–368

    Article  MathSciNet  Google Scholar 

  7. Banifatemi E, Razzaghi M, Yousefi S (2007) Two-dimensional Legendre Wavelets method for the mixed Volterra-Fredholm integral equations. J Vib Control 13(11):1667–1675

    Article  MathSciNet  Google Scholar 

  8. Chen Y, McKenna PJ (1997) Traveling waves in a nonlinear suspension beam: theoretical results and numerical observations. J Differ Equ 135:325–355

    Article  Google Scholar 

  9. Gupta CP (1988) Existence and uniqueness theorem for the bending of an elastic beam equation. Appl Anal 26:289–304

    Article  MathSciNet  Google Scholar 

  10. Heydari MH, Hooshmandasl MR, Cattani C, Li M (2013) Legendre wavelets method for solving fractional population growth model in a closed system. Mathematical Problems in Engineering, Article ID 161030, 8 pages

  11. Islam S, Aziz I, Ahmad M (2015) Numerical solution of two-dimensional elliptic PDEs with nonlocal boundary conditions. Comput Math Appl 69:180–205

    Article  MathSciNet  Google Scholar 

  12. Kumar KH, Vijesh VA (2016) Chebyshev wavelet quasilinearization scheme for coupled nonlinear Sine-Gordon equations. J Comput Nonlinear Dyn 12(1):011018 05 pages

    Article  Google Scholar 

  13. Lazer AC, McKenna PJ (1990) Large-amplitude periodic oscillations in suspension bridges: some new connections with nonlinear analysis. SIAM Rev 32:537–578

    Article  MathSciNet  Google Scholar 

  14. Sunny LA, Vijesh VA (2018) A monotone iterative technique for nonlinear fourth order elliptic equations with nonlocal boundary conditions. J Sci Comput 76:275–298

    Article  MathSciNet  Google Scholar 

  15. McKenna PJ, Walter W (1990) Traveling waves in a suspension bridge. SIAM J Appl Math 50:703–715

    Article  MathSciNet  Google Scholar 

  16. Mohammadi F, Hosseini MM (2011) A new Legendre wavelet operational matrix of derivative and its applications in solving the singular ordinary differential equations. J Franklin Inst 348:1787–1796

    Article  MathSciNet  Google Scholar 

  17. Pao CV, Wang YM (2016) Numerical methods for fourth-order elliptic equations with nonlocal boundary conditions. J Comput Appl Math 292:447–468

    Article  MathSciNet  Google Scholar 

  18. Pao CV, Wang YM (2010) Nonlinear fourth-order elliptic equations with nonlocal boundary conditions. J Math Anal Appl 372:351–365

    Article  MathSciNet  Google Scholar 

  19. Razzaghi M, Yousefi S (2001) The Legendre wavelets operational matrix of integration. Int J Syst Sci 32(4):495–502

    Article  MathSciNet  Google Scholar 

  20. Saeed U, Rehman MU, Iqbal MA (2015) Modified Chebyshev wavelet methods for fractional delay-type equations. Appl Math Comput 264:431–442

    Article  MathSciNet  Google Scholar 

  21. Vijesh VA, Sunny LA, Kumar KH (2016) Legendre wavelet-quasilinearization technique for solving q-difference equations. J Diff Equ Appl 22(4):594–606

    Article  MathSciNet  Google Scholar 

  22. Vijesh A, Kumar KH (2015) Wavelet based quasilinearization method for semi-linear parabolic initial boundary value problem. Appl Math Comput 266:1163–1176

    Article  MathSciNet  Google Scholar 

  23. Yin F, Song J (2014) A coupled method of Laplace transform and Legendre wavelets for nonlinear Klein–Gordon equations. Math Methods Appl Sci 37(6):781–792

    Article  MathSciNet  Google Scholar 

  24. Zhang X, Liu L (2007) Positive solutions of fourth-order multi-point boundary value problems with bending term. Appl Math Comput 194:321–332

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Basic Sciences, Indian Institute of Technology Indore, Indore, 453552, India

    K. Harish Kumar & V. Antony Vijesh

Authors
  1. K. Harish Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. V. Antony Vijesh
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to K. Harish Kumar.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, K.H., Vijesh, V.A. Legendre wavelet-based iterative schemes for fourth-order elliptic equations with nonlocal boundary conditions. Engineering with Computers 36, 1371–1378 (2020). https://doi.org/10.1007/s00366-019-00766-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00766-5

Keywords