Skip to main content
Springer Nature Link
Log in

Nonlinear vibration and dynamic instability analysis nanobeams under thermo-magneto-mechanical loads: a parametric excitation study

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

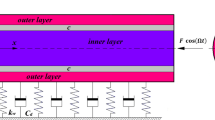
The nonlinear vibration behavior and dynamic instability of Euler–Bernoulli nanobeams under thermo-magneto-mechanical loads is the main objective of the present paper. Firstly, a short Euler–Bernoulli nanobeam is modeled and exposed to an external parametric excitation. Based on the nonlocal continuum theory and nonlinear von Karman beam theory, the nonlinear governing differential equation of motion is derived. Secondly, to transport the partial differential equation to the ordinary differential equation, Galerkin method is applied. Then, multiple scales method, as an analytical approach, is used to solve the equation. At the end, modulation equation of Euler–Bernoulli nanobeams is obtained. Then, to evaluate the dynamic instability of the system, trivial and nontrivial steady-state solutions are discussed. Emphasizing the effect of parametric excitation, for considering the instability regions, bifurcation points are studied and investigated. As a result, it can be observed that the damping coefficient plays an effective role as well as parametric excitation in stability and frequency response of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Eda G, Fanchini G, Chhowalla M (2008) Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material. Nat Nanotechnol 3(5):270

    Google Scholar 

  2. Li D, Müller MB, Gilje S, Kaner RB, Wallace GG (2008) Processable aqueous dispersions of graphene nanosheets. Nat Nanotechnol 3(2):101

    Google Scholar 

  3. Potekin R, Kim S, McFarland DM, Bergman LA, Cho H, Vakakis AF (2018) A micromechanical mass sensing method based on amplitude tracking within an ultra-wide broadband resonance. Nonlinear Dyn 92(2):287–304

    Google Scholar 

  4. Mahmoud MA (2016) Validity and accuracy of resonance shift prediction formulas for microcantilevers: a review and comparative study. Crit Rev Solid State Mater Sci 41(5):386–429

    Google Scholar 

  5. Ji Y, Choe M, Cho B, Song S, Yoon J, Ko HC, Lee T (2012) Organic nonvolatile memory devices with charge trapping multilayer graphene film. Nanotechnology 23(10):105202

    Google Scholar 

  6. Arash B, Wang Q (2013) Detection of gas atoms with carbon nanotubes. Sci Rep 3:1782

    Google Scholar 

  7. Bunch JS, Van Der Zande AM, Verbridge SS, Frank IW, Tanenbaum DM, Parpia JM, McEuen PL (2007) Electromechanical resonators from graphene sheets. Science 315(5811):490–493

    Google Scholar 

  8. Kuilla T, Bhadra S, Yao D, Kim NH, Bose S, Lee JH (2010) Recent advances in graphene based polymer composites. Prog Polym Sci 35(11):1350–1375

    Google Scholar 

  9. Eringen AC, Edelen DGB (1972) On nonlocal elasticity. Int J Eng Sci 10(3):233–248

    MathSciNet  MATH  Google Scholar 

  10. Eringen AC (1983) Theories of nonlocal plasticity. Int J Eng Sci 21(7):741–751

    MATH  Google Scholar 

  11. Ghadiri M, Shafiei N, Akbarshahi A (2016) Influence of thermal and surface effects on vibration behavior of nonlocal rotating Timoshenko nanobeam. Appl Phys A 122(7):673

    Google Scholar 

  12. Rahmanian S, Ghazavi MR, Hosseini-Hashemi S (2019) On the numerical investigation of size and surface effects on nonlinear dynamics of a nanoresonator under electrostatic actuation. J Braz Soc Mech Sci Eng 41(1):16

    Google Scholar 

  13. Zhang YQ, Liu GR, Wang JS (2004) Small-scale effects on buckling of multiwalled carbon nanotubes under axial compression. Phys Rev B 70(20):205430

    Google Scholar 

  14. Barretta R, Feo L, Luciano R, de Sciarra FM (2015) Variational formulations for functionally graded nonlocal Bernoulli–Euler nanobeams. Compos Struct 129:80–89

    Google Scholar 

  15. Ghadiri M, Safi M (2017) Nonlinear vibration analysis of functionally graded nanobeam using homotopy perturbation method. Adv Appl Math Mech 9(1):144–156

    MathSciNet  Google Scholar 

  16. Ehyaei J, Akbarshahi A, Shafiei N (2017) Influence of porosity and axial preload on vibration behavior of rotating FG nanobeam. Adv Nano Res 5(2):141–169

    Google Scholar 

  17. Ebrahimi F, Hosseini SHS (2016) Thermal effects on nonlinear vibration behavior of viscoelastic nanosize plates. J Therm Stresses 39(5):606–625

    Google Scholar 

  18. Mouffoki A, Bedia EA, Houari MSA, Tounsi A, Mahmoud SR (2017) Vibration analysis of nonlocal advanced nanobeams in hygro-thermal environment using a new two-unknown trigonometric shear deformation beam theory. Smart Struct Syst 20(3):369–383

    Google Scholar 

  19. Bedia WA, Houari MSA, Bessaim A, Bousahla AA, Tounsi A, Saeed T, Alhodaly MS (2019) A new hyperbolic two-unknown beam model for bending and buckling analysis of a nonlocal strain gradient nanobeams. J Nano Res 57:175–191

    Google Scholar 

  20. Mokhtar Y, Heireche H, Bousahla AA, Houari MSA, Tounsi A, Mahmoud SR (2018) A novel shear deformation theory for buckling analysis of single layer graphene sheet based on nonlocal elasticity theory. Smart Struct Syst 21(4):397–405

    Google Scholar 

  21. Bellifa H, Benrahou KH, Bousahla AA, Tounsi A, Mahmoud SR (2017) A nonlocal zeroth-order shear deformation theory for nonlinear postbuckling of nanobeams. Struct Eng Mech 62(6):695–702

    Google Scholar 

  22. Zemri A, Houari MSA, Bousahla AA, Tounsi A (2015) A mechanical response of functionally graded nanoscale beam: an assessment of a refined nonlocal shear deformation theory beam theory. Struct Eng Mech 54(4):693–710

    Google Scholar 

  23. Bouafia K, Kaci A, Houari MSA, Benzair A, Tounsi A (2017) A nonlocal quasi-3D theory for bending and free flexural vibration behaviors of functionally graded nanobeams. Smart Struct Syst 19(2):115–126

    Google Scholar 

  24. Kadari B, Bessaim A, Tounsi A, Heireche H, Bousahla AA, Houari MSA (2018) Buckling analysis of orthotropic nanoscale plates resting on elastic foundations. J Nano Res 55:42–56

    Google Scholar 

  25. Karami B, Janghorban M, Tounsi A (2018) Variational approach for wave dispersion in anisotropic doubly-curved nanoshells based on a new nonlocal strain gradient higher order shell theory. Thin Walled Struct 129:251–264

    Google Scholar 

  26. Karami B, Janghorban M, Tounsi A (2018) Nonlocal strain gradient 3D elasticity theory for anisotropic spherical nanoparticles. Steel Compos Struct 27(2):201–216

    Google Scholar 

  27. Karami B, Janghorban M, Shahsavari D, Tounsi A (2018) A size-dependent quasi-3D model for wave dispersion analysis of FG nanoplates. Steel Compos Struct 28(1):99–110

    Google Scholar 

  28. Karami B, Janghorban M, Tounsi A (2017) Effects of triaxial magnetic field on the anisotropic nanoplates. Steel Compos Struct 25(3):361–374

    Google Scholar 

  29. Karami B, Shahsavari D, Nazemosadat SMR, Li L, Ebrahimi A (2018) Thermal buckling of smart porous functionally graded nanobeam rested on Kerr foundation. Steel Compos Struct 29(3):349–362

    Google Scholar 

  30. Ahouel M, Houari MSA, Bedia EA, Tounsi A (2016) Size-dependent mechanical behavior of functionally graded trigonometric shear deformable nanobeams including neutral surface position concept. Steel Compos Struct 20(5):963–981

    Google Scholar 

  31. Chaht FL, Kaci A, Houari MSA, Tounsi A, Bég OA, Mahmoud SR (2015) Bending and buckling analyses of functionally graded material (FGM) size-dependent nanoscale beams including the thickness stretching effect. Steel Compos Struct 18(2):425–442

    Google Scholar 

  32. Tlidji Y, Zidour M, Draiche K, Safa A, Bourada M, Tounsi A, Mahmoud SR (2019) Vibration analysis of different material distributions of functionally graded microbeam. Struct Eng Mech 69(6):637–649

    Google Scholar 

  33. Abualnour M, Houari MSA, Tounsi A, Mahmoud SR (2018) A novel quasi-3D trigonometric plate theory for free vibration analysis of advanced composite plates. Compos Struct 184:688–697

    Google Scholar 

  34. Chikh A, Tounsi A, Hebali H, Mahmoud SR (2017) Thermal buckling analysis of cross-ply laminated plates using a simplified HSDT. Smart Struct Syst 19(3):289–297

    Google Scholar 

  35. Semmah A, Heireche H, Bousahla AA, Tounsi A (2019) Thermal buckling analysis of SWBNNT on Winkler foundation by nonlocal FSDT. Adv Nano Res 7(2):89–98

    Google Scholar 

  36. Hamza-Cherif R, Meradjah M, Zidour M, Tounsi A, Belmahi S, Bensattalah T (2018) Vibration analysis of nano beam using differential transform method including thermal effect. J Nano Res 54:1–14

    Google Scholar 

  37. Şimşek M (2014) Large amplitude free vibration of nanobeams with various boundary conditions based on the nonlocal elasticity theory. Compos B Eng 56:621–628

    Google Scholar 

  38. Şimşek M (2016) Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. Int J Eng Sci 105:12–27

    MathSciNet  MATH  Google Scholar 

  39. Nazemnezhad R, Hosseini-Hashemi S (2014) Nonlocal nonlinear free vibration of functionally graded nanobeams. Compos Struct 110:192–199

    MATH  Google Scholar 

  40. Nourbakhsh H, Mohammadzadeh R, Rafiee M, Rafiee R (2012) Nonlinear effects on resonance behaviour of beams in micro scale. Appl Mech Mater 110:4178–4186

    Google Scholar 

  41. Oskouie MF, Ansari R, Sadeghi F (2017) Nonlinear vibration analysis of fractional viscoelastic Euler–Bernoulli nanobeams based on the surface stress theory. Acta Mech Solida Sin 30(4):416–424

    Google Scholar 

  42. Ghadiri M, Rajabpour A, Akbarshahi A (2017) Non-linear forced vibration analysis of nanobeams subjected to moving concentrated load resting on a viscoelastic foundation considering thermal and surface effects. Appl Math Model 50:676–694

    MathSciNet  MATH  Google Scholar 

  43. Attia A, Bousahla AA, Tounsi A, Mahmoud SR, Alwabli AS (2018) A refined four variable plate theory for thermoelastic analysis of FGM plates resting on variable elastic foundations. Struct Eng Mech 65(4):453–464

    Google Scholar 

  44. Menasria A, Bouhadra A, Tounsi A, Bousahla AA, Mahmoud SR (2017) A new and simple HSDT for thermal stability analysis of FG sandwich plates. Steel Compos Struct 25(2):157–175

    Google Scholar 

  45. El-Haina F, Bakora A, Bousahla AA, Tounsi A, Mahmoud SR (2017) A simple analytical approach for thermal buckling of thick functionally graded sandwich plates. Struct Eng Mech 63(5):585–595

    Google Scholar 

  46. Bousahla AA, Benyoucef S, Tounsi A, Mahmoud SR (2016) On thermal stability of plates with functionally graded coefficient of thermal expansion. Struct Eng Mech 60(2):313–335

    Google Scholar 

  47. Bouderba B, Houari MSA, Tounsi A, Mahmoud SR (2016) Thermal stability of functionally graded sandwich plates using a simple shear deformation theory. Struct Eng Mech 58(3):397–422

    Google Scholar 

  48. Khetir H, Bouiadjra MB, Houari MSA, Tounsi A, Mahmoud SR (2017) A new nonlocal trigonometric shear deformation theory for thermal buckling analysis of embedded nanosize FG plates. Struct Eng Mech 64(4):391–402

    Google Scholar 

  49. Fahsi A, Tounsi A, Hebali H, Chikh A, Adda Bedia EA, Mahmoud SR (2017) A four variable refined nth-order shear deformation theory for mechanical and thermal buckling analysis of functionally graded plates. Geomech Eng 13(3):385–410

    Google Scholar 

  50. Beldjelili Y, Tounsi A, Mahmoud SR (2016) Hygro-thermo-mechanical bending of S-FGM plates resting on variable elastic foundations using a four-variable trigonometric plate theory. Smart Struct Syst 18(4):755–786

    Google Scholar 

  51. Hamidi A, Houari MSA, Mahmoud SR, Tounsi A (2015) A sinusoidal plate theory with 5-unknowns and stretching effect for thermomechanical bending of functionally graded sandwich plates. Steel Compos Struct 18(1):235–253

    Google Scholar 

  52. Belkorissat I, Houari MSA, Tounsi A, Bedia EA, Mahmoud SR (2015) On vibration properties of functionally graded nano-plate using a new nonlocal refined four variable model. Steel Compos Struct 18(4):1063–1081

    Google Scholar 

  53. Bourada F, Bousahla AA, Bourada M, Azzaz A, Zinata A, Tounsi A (2019) Dynamic investigation of porous functionally graded beam using a sinusoidal shear deformation theory. Wind Struct 28(1):19–30

    Google Scholar 

  54. Abdelaziz HH, Meziane MAA, Bousahla AA, Tounsi A, Mahmoud SR, Alwabli AS (2017) An efficient hyperbolic shear deformation theory for bending, buckling and free vibration of FGM sandwich plates with various boundary conditions. Steel Compos Struct 25(6):693–704

    Google Scholar 

  55. Meksi R, Benyoucef S, Mahmoudi A, Tounsi A, Adda Bedia EA, Mahmoud SR (2019) An analytical solution for bending, buckling and vibration responses of FGM sandwich plates. J Sandw Struct Mater 21(2):727–757

    Google Scholar 

  56. Younsi A, Tounsi A, Zaoui FZ, Bousahla AA, Mahmoud SR (2018) Novel quasi-3D and 2D shear deformation theories for bending and free vibration analysis of FGM plates. Geomech Eng 14(6):519–532

    Google Scholar 

  57. Zaoui FZ, Ouinas D, Tounsi A (2019) New 2D and quasi-3D shear deformation theories for free vibration of functionally graded plates on elastic foundations. Compos B Eng 159:231–247

    Google Scholar 

  58. Belabed Z, Bousahla AA, Houari MSA, Tounsi A, Mahmoud SR (2018) A new 3-unknown hyperbolic shear deformation theory for vibration of functionally graded sandwich plate. Earthq Struct 14(2):103–115

    Google Scholar 

  59. Houari MSA, Tounsi A, Bessaim A, Mahmoud SR (2016) A new simple three-unknown sinusoidal shear deformation theory for functionally graded plates. Steel Compos Struct 22(2):257–276

    Google Scholar 

  60. Karami B, Shahsavari D, Janghorban M, Tounsi A (2019) Resonance behavior of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Int J Mech Sci 156:94–105

    Google Scholar 

  61. Besseghier A, Houari MSA, Tounsi A, Mahmoud SR (2017) Free vibration analysis of embedded nanosize FG plates using a new nonlocal trigonometric shear deformation theory. Smart Struct Syst 19(6):601–614

    Google Scholar 

  62. Bounouara F, Benrahou KH, Belkorissat I, Tounsi A (2016) A nonlocal zeroth-order shear deformation theory for free vibration of functionally graded nanoscale plates resting on elastic foundation. Steel Compos Struct 20(2):227–249

    Google Scholar 

  63. She GL, Yuan FG, Ren YR, Xiao WS (2017) On buckling and postbuckling behavior of nanotubes. Int J Eng Sci 121:130–142

    MathSciNet  MATH  Google Scholar 

  64. She GL, Yuan FG, Ren YR, Liu HB, Xiao WS (2018) Nonlinear bending and vibration analysis of functionally graded porous tubes via a nonlocal strain gradient theory. Compos Struct 203:614–623

    Google Scholar 

  65. She GL, Ren YR, Yuan FG, Xiao WS (2018) On vibrations of porous nanotubes. Int J Eng Sci 125:23–35

    MathSciNet  MATH  Google Scholar 

  66. She GL, Ren YR, Yan KM (2019) On snap-buckling of porous FG curved nanobeams. Acta Astronaut 161:475–484

    Google Scholar 

  67. She GL, Yuan FG, Ren YR (2018) On wave propagation of porous nanotubes. Int J Eng Sci 130:62–74

    MathSciNet  MATH  Google Scholar 

  68. Fourn H, Atmane HA, Bourada M, Bousahla AA, Tounsi A, Mahmoud SR (2018) A novel four variable refined plate theory for wave propagation in functionally graded material plates. Steel Compos Struct 27(1):109–122

    Google Scholar 

  69. Bouhadra A, Tounsi A, Bousahla AA, Benyoucef S, Mahmoud SR (2018) Improved HSDT accounting for effect of thickness stretching in advanced composite plates. Struct Eng Mech 66(1):61–73

    Google Scholar 

  70. de Oliveira FM, Greco M (2015) Nonlinear dynamic analysis of beams with layered cross sections under moving masses. J Braz Soc Mech Sci Eng 37(2):451–462

    Google Scholar 

  71. Arani AG, Abdollahian M, Kolahchi R (2015) Nonlinear vibration of a nanobeam elastically bonded with a piezoelectric nanobeam via strain gradient theory. Int J Mech Sci 100:32–40

    Google Scholar 

  72. Huang Y, Fu J, Liu A (2018) Dynamic instability of Euler–Bernoulli nanobeams subject to parametric excitation. Compos B Eng 164:226–234

    Google Scholar 

  73. Wang YZ, Wang YS, Ke LL (2016) Nonlinear vibration of carbon nanotube embedded in viscous elastic matrix under parametric excitation by nonlocal continuum theory. Physica E 83:195–200

    Google Scholar 

  74. Li C, Lim CW, Yu JL (2010) Dynamics and stability of transverse vibrations of nonlocal nanobeams with a variable axial load. Smart Mater Struct 20(1):015023

    Google Scholar 

  75. Bakhadda B, Bouiadjra MB, Bourada F, Bousahla AA, Tounsi A, Mahmoud SR (2018) Dynamic and bending analysis of carbon nanotube-reinforced composite plates with elastic foundation. Wind Struct 27(5):311–324

    Google Scholar 

  76. Bouadi A, Bousahla AA, Houari MSA, Heireche H, Tounsi A (2018) A new nonlocal HSDT for analysis of stability of single layer graphene sheet. Adv Nano Res 6(2):147–162

    Google Scholar 

  77. Yazid M, Heireche H, Tounsi A, Bousahla AA, Houari MSA (2018) A novel nonlocal refined plate theory for stability response of orthotropic single-layer graphene sheet resting on elastic medium. Smart Struct Syst 21(1):15–25

    Google Scholar 

  78. Youcef DO, Kaci A, Benzair A, Bousahla AA, Tounsi A (2018) Dynamic analysis of nanoscale beams including surface stress effects. Smart Struct Syst 21(1):65–74

    Google Scholar 

  79. Draoui A, Zidour M, Tounsi A, Adim B (2019) Static and dynamic behavior of nanotubes-reinforced sandwich plates using (FSDT). J Nano Res 57:117–135

    Google Scholar 

  80. Alevras P, Theodossiades S, Rahnejat H (2017) Broadband energy harvesting from parametric vibrations of a class of nonlinear Mathieu systems. Appl Phys Lett 110(23):233901

    Google Scholar 

  81. Amer YA, El-Sayed AT, Kotb AA (2016) Nonlinear vibration and of the Duffing oscillator to parametric excitation with time delay feedback. Nonlinear Dyn 85(4):2497–2505

    MathSciNet  Google Scholar 

  82. Bobryk RV, Yurchenko D (2016) On enhancement of vibration-based energy harvesting by a random parametric excitation. J Sound Vib 366:407–417

    Google Scholar 

  83. Darabi M, Ganesan R (2017) Non-linear vibration and dynamic instability of internally-thickness-tapered composite plates under parametric excitation. Compos Struct 176:82–104

    Google Scholar 

  84. Wang YZ (2017) Nonlinear internal resonance of double-walled nanobeams under parametric excitation by nonlocal continuum theory. Appl Math Model 48:621–634

    MathSciNet  MATH  Google Scholar 

  85. Krylov S, Harari I, Cohen Y (2005) Stabilization of electrostatically actuated microstructures using parametric excitation. J Micromech Microeng 15(6):1188

    Google Scholar 

  86. Lima R, Sampaio R (2016) Two parametric excited nonlinear systems due to electromechanical coupling. J Braz Soc Mech Sci Eng 38(3):931–943

    Google Scholar 

  87. Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16

    MathSciNet  MATH  Google Scholar 

  88. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710

    Google Scholar 

  89. Emam SA (2009) A static and dynamic analysis of the postbuckling of geometrically imperfect composite beams. Compos Struct 90(2):247–253

    MathSciNet  Google Scholar 

  90. Emam SA, Nayfeh AH (2009) Postbuckling and free vibrations of composite beams. Compos Struct 88(4):636–642

    Google Scholar 

  91. Murmu T, McCarthy MA, Adhikari S (2013) In-plane magnetic field affected transverse vibration of embedded single-layer graphene sheets using equivalent nonlocal elasticity approach. Compos Struct 96:57–63

    Google Scholar 

  92. Kitipornchai S, He XQ, Liew KM (2005) Continuum model for the vibration of multilayered graphene sheets. Phys Rev B 72(7):075443

    Google Scholar 

  93. Nayfeh AH, Mook DT (2008) Nonlinear oscillations. Wiley, New York

    MATH  Google Scholar 

  94. Azrar L, Benamar R, White RG (1999) Semi-analytical approach to the non-linear dynamic response problem of S–S and C–C beams at large vibration amplitudes part I: general theory and application to the single mode approach to free and forced vibration analysis. J Sound Vib 224(2):183–207

    Google Scholar 

  95. Azrar L, Benamar R, White RG (2002) A semi-analytical approach to the non-linear dynamic response problem of beams at large vibration amplitudes, Part II: multimode approach to the steady state forced periodic response. J Sound Vib 255(1):1–41

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Qazvin, 3414896818, Iran

    Farzad Ebrahimi & S. Hamed S. Hosseini

Authors
  1. Farzad Ebrahimi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Hamed S. Hosseini
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, F., Hosseini, S.H.S. Nonlinear vibration and dynamic instability analysis nanobeams under thermo-magneto-mechanical loads: a parametric excitation study. Engineering with Computers 37, 395–408 (2021). https://doi.org/10.1007/s00366-019-00830-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00830-0

Keywords