Skip to main content
Springer Nature Link
Log in

I-GWO and Ex-GWO: improved algorithms of the Grey Wolf Optimizer to solve global optimization problems

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

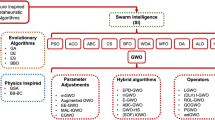
In this paper, two novel meta-heuristic algorithms are introduced to solve global optimization problems inspired by the Grey Wolf Optimizer (GWO) algorithm. In the GWO algorithm, wolves are likely to be located in regions close to each other. Therefore, as they catch the hunt (approaching the solution), they may create an intensity in the same or certain regions. In this case, the mechanism to prevent the escape of the hunt may not work well. First, the proposed algorithm is the expanded model of the GWO algorithm that is called expanded Grey Wolf Optimizer. In this method, the same as GWO, alpha, beta, and delta play the role of the main three wolves. However, the next wolves select and update their positions according to the previous and the first three wolves in each iteration. Another proposed algorithm is based on the incremental model and is, therefore, called incremental Grey Wolf Optimizer. In this method, each wolf updates its own position based on all the wolves selected before it. There is the possibility of finding solutions (hunts) quicker than according to other algorithms in the same category. However, they may not always guarantee to find a good solution because of their act dependent on each other. Both algorithms focus on exploration and exploitation. In this paper, the proposed algorithms are simulated over 33 benchmark functions and the related results are compared with well-known optimization algorithms. The results of the proposed algorithms seem to be good solutions for various problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Winston PH (1992) Artificial intelligence, 3rd edn. Addison-Wesley, Boston

    MATH  Google Scholar 

  2. Yao X, Yong L (1997) Fast evolution strategies. In: International conference on evolutionary programming. Springer, Berlin

  3. Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61

    Google Scholar 

  4. Talbi EG (2009) Metaheuristics: from design to implementation, vol 74. Wiley, Hoboken

    MATH  Google Scholar 

  5. Mirjalili S (2015) The ant lion optimizer. Adv Eng Softw 83:80–98

    Google Scholar 

  6. Jamil M, Xin-She Y (2013) A literature survey of benchmark functions for global optimization problems. arXiv preprint arXiv.1308-4008

  7. Holland JH (1992) Genetic algorithms. Sci Am 267(1):66–73

    Google Scholar 

  8. Chawla P, Chana I, Rana A (2015) A novel strategy for automatic test data generation using soft computing technique. Front Comput Sci 9(3):346–363

    Google Scholar 

  9. Gomes GF, de Almeida FA, Junqueira DM, da Cunha Jr SS, Ancelotti AC Jr (2019) Optimized damage identification in CFRP plates by reduced mode shapes and GA-ANN methods. Eng Struct 181:111–123

    Google Scholar 

  10. Kilinc M, Caicedo JM (2019) Finding plausible optimal solutions in engineering problems using an adaptive genetic algorithm. Adv Civ Eng 2019:1–9

    Google Scholar 

  11. Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim 11(4):341–359

    MathSciNet  MATH  Google Scholar 

  12. Sharma R, Vashisht V, Singh AV, Kumar S (2019) Analysis of existing clustering algorithms for wireless sensor networks. System Performance and Management Analytics. Springer, Singapore, pp 259–277

    Google Scholar 

  13. Mann PS, Singh S (2019) Improved metaheuristic-based energy-efficient clustering protocol with optimal base station location in wireless sensor networks. Soft Comput 23(3):1021–1037

    MATH  Google Scholar 

  14. Sahu RK, Sekhar GC, Priyadarshani S (2019) Differential evolution algorithm tuned tilt integral derivative controller with filter controller for automatic generation control. Evol Intell. https://doi.org/10.1007/s12065-019-00215-8

    Article  Google Scholar 

  15. Yao X, Liu Y, Lin G (1999) Evolutionary programming made faster. IEEE Trans Evol Comput 3(2):82–102

    Google Scholar 

  16. Fogel LJ, Owens AJ, Walsh MJ (1966) Artificial intelligence through simulated evolution. Wiley-IEEE Press, Hoboken

    MATH  Google Scholar 

  17. Zhang X, Luo J, Sun X, Xie J (2019) Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm. Eng Optim 51(1):42–62

    MathSciNet  Google Scholar 

  18. Simon D (2008) Biogeography-based optimization. IEEE Trans Evol Comput 12(6):702–713

    Google Scholar 

  19. Kasilingam F, Pasupuleti J, Bharatiraja C, Adedayo Y (2019) Power system stabilizer optimization using BBO algorithm for a better damping of rotor oscillations owing to small disturbances. FME Trans 47(1):166–176

    Google Scholar 

  20. Kumar M, Om H (2019) A Hybrid bio-inspired algorithm for protein domain problems. In: Advances in nature-inspired computing and applications. Springer, Cham, pp 291–311

  21. Bhattacharya A, Chattopadhyay PK (2010) Solving complex economic load dispatch problems using biogeography-based optimization. Expert Syst Appl 37(5):3605–3615

    Google Scholar 

  22. Rashedi E, Nezamabadi-Pour H, Saryazdi S (2009) GSA: a gravitational search algorithm. Inf Sci 179(13):2232–2248

    MATH  Google Scholar 

  23. Naserbegi A, Aghaie M, Minuchehr A, Alahyarizadeh G (2018) A novel exergy optimization of Bushehr nuclear power plant by gravitational search algorithm (GSA). Energy 148:373–385

    Google Scholar 

  24. Marzband M, Ghadimi M, Sumper A, Domínguez-García JL (2014) Experimental validation of a real-time energy management system using multi-period gravitational search algorithm for microgrids in islanded mode. Appl Energy 128:164–174

    Google Scholar 

  25. Chakraborti T, Sharma KD, Chatterjee A (2014) A novel local extrema based gravitational search algorithm and its application in face recognition using one training image per class. Eng Appl Artif Intell 34:13–22

    Google Scholar 

  26. Erol OK, Eksin I (2006) A new optimization method: big bang–big crunch. Adv Eng Softw 37(2):106–111

    Google Scholar 

  27. Sakthivel S, Pandiyan SA, Marikani S, Selvi SK (2013) Application of big bang big crunch algorithm for optimal power flow problems. Int J Eng Sci 2(4):41–47

    Google Scholar 

  28. Kaveh A, Talatahari S (2010) A novel heuristic optimization method: charged system search. Acta Mech 213(3–4):267–289

    MATH  Google Scholar 

  29. Özyön S, Temurtaş H, Durmuş B, Kuvat G (2012) Charged system search algorithm for emission constrained economic power dispatch problem. Energy 46(1):420–430

    Google Scholar 

  30. Lam AY, Li VO (2010) Chemical-reaction-inspired metaheuristic for optimization. IEEE Trans Evol Comput 14(3):381–399

    Google Scholar 

  31. Xu J, Lam AY, Li VO (2011) Chemical reaction optimization for task scheduling in grid computing. IEEE Trans Parallel Distrib Syst 22(10):1624–1631

    Google Scholar 

  32. Li Z, Li Y, Yuan T, Chen S, Jiang S (2019) Chemical reaction optimization for virtual machine placement in cloud computing. Appl Intell 49(1):220–232

    Google Scholar 

  33. Kabir R, Islam R (2019) Chemical reaction optimization for RNA structure prediction. Appl Intell 49(2):352–375

    Google Scholar 

  34. Formato RA (2007) Central force optimization: a new metaheuristic with applications in applied electromagnetics. Prog Electromagn Res 77:425–491

    Google Scholar 

  35. Haghighi A, Ramos HM (2012) Detection of leakage freshwater and friction factor calibration in drinking networks using central force optimization. Water Resour Manag 26(8):2347–2363

    Google Scholar 

  36. Hatamlou A (2013) Black hole: a new heuristic optimization approach for data clustering. Inf Sci 222:175–184

    MathSciNet  Google Scholar 

  37. Hatamlou A (2018) Solving travelling salesman problem using black hole algorithm. Soft Comput 22(24):8167–8175

    Google Scholar 

  38. Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of ICNN'95 - international conference on neural networks, Australia, pp 1942–1948

  39. Pattanayak S, Agarwal S, Choudhury BB, Sahoo SC (2019) Path planning of mobile robot using PSO algorithm. In: Information and communication technology for intelligent systems. Springer, Singapore, pp 515–522

  40. Syahputra R, Robandi I, Ashari M (2015) Reconfiguration of distribution network with distributed energy resources integration using PSO algorithm. Telkomnika 13(3):759

    Google Scholar 

  41. Dorigo M, Birattari M (2010) Ant colony optimization. Springer, New York, pp 36–39

    Google Scholar 

  42. Okdem S, Karaboga D (2009) Routing in wireless sensor networks using an ant colony optimization (ACO) router chip. Sensors 9(2):909–921

    Google Scholar 

  43. Yi W, Kumar A (2007) Ant colony optimization for disaster relief operations. Transp Res Part E Logist Transp Rev 43(6):660–672

    Google Scholar 

  44. Tian J, Yu W, Xie S (2008) An ant colony optimization algorithm for image edge detection. In: 2008 IEEE congress on evolutionary computation (IEEE World Congress on Computational Intelligence). IEEE, pp 751–756

  45. Karaboga D, Basturk B (2008) On the performance of artificial bee colony (ABC) algorithm. Appl Soft Comput 8(1):687–697

    Google Scholar 

  46. Gong D, Han Y, Sun J (2018) A novel hybrid multi-objective artificial bee colony algorithm for blocking lot-streaming flow shop scheduling problems. Knowl Based Syst 148:115–130

    Google Scholar 

  47. Singh A (2009) An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem. Appl Soft Comput 9(2):625–631

    Google Scholar 

  48. Yang XS (2010) A new metaheuristic bat-inspired algorithm. Nature inspired cooperative strategies for optimization (NICSO 2010). Springer, New York, pp 65–74

    Google Scholar 

  49. Osaba E, Yang XS, Diaz F, Lopez-Garcia P, Carballedo R (2016) An improved discrete bat algorithm for symmetric and asymmetric traveling salesman problems. Eng Appl Artif Intell 48:59–71

    Google Scholar 

  50. Sathya MR, Ansari MMT (2015) Load frequency control using Bat inspired algorithm based dual mode gain scheduling of PI controllers for interconnected power system. Int J Electr Power Energy Syst 64:365–374

    Google Scholar 

  51. Yang XS (2010) Firefly algorithm, stochastic test functions and design optimisation. Int J Bio-Inspir Comput 2:78–84

    Google Scholar 

  52. Banati H, Bajaj M (2011) Fire fly based feature selection approach. Int J Comput Sci Issues (IJCSI) 8(4):473

    Google Scholar 

  53. Talatahari S, Gandomi AH, Yun GJ (2014) Optimum design of tower structures using firefly algorithm. Struct Des Tall Spec Build 23(5):350–361

    Google Scholar 

  54. Tuba E, Tuba M, Beko M (2017) Mobile wireless sensor networks coverage maximization by firefly algorithm. In: 2017 27th international conference Radioelektronika (RADIOELEKTRONIKA). IEEE, pp 1–5

  55. Yang XS, Deb S (2009) Cuckoo search via Lévy flights. In: 2009 World congress on nature and biologically inspired computing (NaBIC), pp 210–214

  56. Mohamad A, Zain AM, Bazin NEN, Udin A (2013) Cuckoo search algorithm for optimization problems-a literature review. Applied mechanics and materials, vol 421. Trans Tech Publications, Zurich, pp 502–506

    Google Scholar 

  57. Rath A, Samantaray S, Swain PC (2019) Optimization of the cropping pattern using cuckoo search technique. Smart techniques for a smarter planet. Springer, Cham, pp 19–35

    Google Scholar 

  58. Arif MA, Mohamad MS, Latif MSA, Deris S, Remli MA, Daud KM, Corchado JM (2018) A hybrid of cuckoo search and minimization of metabolic adjustment to optimize metabolites production in genome-scale models. Comput Biol Med 102:112–119

    Google Scholar 

  59. Dhivya M, Sundarambal M (2011) Cuckoo search for data gathering in wireless sensor networks. Int J Mob Commun 9(6):642–656

    Google Scholar 

  60. Mucherino A, Seref O (2007) Monkey search: a novel metaheuristic search for global optimization. AIP Conf Proc 953(1):162–173

    Google Scholar 

  61. Zhou Y, Chen X, Zhou G (2016) An improved monkey algorithm for a 0–1 knapsack problem. Appl Soft Comput 38:817–830

    Google Scholar 

  62. Yi TH, Li HN, Zhang XD (2015) Health monitoring sensor placement optimization for Canton Tower using immune monkey algorithm. Struct Control Health Monit 22(1):123–138

    Google Scholar 

  63. Khairuzzaman AKM, Chaudhury S (2017) Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst Appl 86:64–76

    Google Scholar 

  64. Li Q, Chen H, Huang H, Zhao X, Cai Z, Tong C, Tian X (2017) An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis. Comput Math Methods Med 2017:1–15

    Google Scholar 

  65. Fahad M, Aadil F, Khan S, Shah PA, Muhammad K, Lloret J, Mehmood I (2018) Grey wolf optimization based clustering algorithm for vehicular ad-hoc networks. Comput Electr Eng 70:853–870

    Google Scholar 

  66. Mousavi S, Mosavi A, Varkonyi-Koczy AR (2017) A load balancing algorithm for resource allocation in cloud computing. In: International conference on global research and education. Springer, Cham, pp 289–296

  67. Mittal N, Singh U, Sohi BS (2016) Modified grey wolf optimizer for global engineering optimization. Appl Comput Intell Soft Comput 8:1–16

    Google Scholar 

  68. Faris H, Aljarah I, Al-Betar MA, Mirjalili S (2018) Grey wolf optimizer: a review of recent variants and applications. Neural Comput Appl 30(2):413–435

    Google Scholar 

  69. Joshi H, Arora S (2017) Enhanced grey wolf optimization algorithm for global optimization. Fundam Inform 153(3):235–264

    MathSciNet  MATH  Google Scholar 

  70. Liang JJ, Qu BY, Suganthan PN (2013) Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou China and Technical Report, Nanyang Technological University, Singapore, vol 635

  71. Liang JJ, Qu BY, Suganthan PN, Chen Q (2014) Problem definitions and evaluation criteria for the CEC 2015 competition on learning-based real-parameter single objective optimization. Technical Report201411A, Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou China and Technical Report, Nanyang Technological University, Singapore, vol 29, pp 625–640

  72. Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computer Engineering Department, Engineering and Natural Sciences Faculty, Istanbul Sabahattin Zaim University, Istanbul, Turkey

    Amir Seyyedabbasi

  2. Computer Engineering Department, Engineering and Architecture Faculty, Istanbul Arel University, Istanbul, Turkey

    Farzad Kiani

Authors
  1. Amir Seyyedabbasi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Farzad Kiani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Amir Seyyedabbasi.

Ethics declarations

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Seyyedabbasi, A., Kiani, F. I-GWO and Ex-GWO: improved algorithms of the Grey Wolf Optimizer to solve global optimization problems. Engineering with Computers 37, 509–532 (2021). https://doi.org/10.1007/s00366-019-00837-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00837-7

Keywords