Skip to main content

Advertisement

Springer Nature Link
Log in

Nonlinear free vibration analysis of composite conical shell panel with cluster of delamination in hygrothermal environment

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

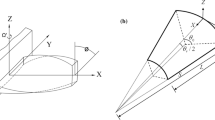
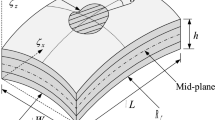
The nonlinear eigenvalue responses of conical composite shell structure with cluster of multiple delaminations are investigated numerically using the displacement-type finite element technique including the influence of the moisture and elevated thermal environment. The governing equation for the free vibrated structure case of the layered conical panel is obtained through a generalization of the principle of virtual displacement. The numerical solutions are obtained through a customized computer code developed via the higher order displacement field model imposing the zero stresses at the top and bottom surfaces of the laminate. The panel model has been discretized using an eight-nodded isoparametric element to maintain the desired C0 continuity and to avoid the mathematical complexity involved in C1-type continuity. A delamination model is developed by accounting single and cluster of delaminations. The delamination is located at centre of the laminates, either in cluster form or segregated over the lamina. The model is developed by considering the laminate is exposed to elevated moisture and temperature environment. The contribution of moisture and temperature effects on delaminated lamina is examined. The solution methodology is validated with published results. Influence of various parameters such as lamination schemes, aspect ratios, support conditions, thickness ratios, curvature ratios and material properties of the linear and nonlinear free vibration frequencies are analysed in detail and presented. The inferences from the study signify the reduction trend of fundamental frequency due to the presence of single/multi-delamination and moisture content.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Barbero EJ, Reddy JN (1991) Modeling of delamination in composite laminates using a layer-wise plate theory. Int J Solids Struct 28:373–388. https://doi.org/10.1016/0020-7683(91)90200-Y

    Article  MATH  Google Scholar 

  2. Jinho O, Cho M, Kim JS (2005) Dynamic analysis of composite plate with multiple delaminations based on higher-order zigzag theory. Int J Solids Struct 42:6122–6140. https://doi.org/10.1016/j.ijsolstr.2005.06.006

    Article  MATH  Google Scholar 

  3. Parhi PK, Bhattaacharyya SK, Sinha PK (2001) Hygrothermal effects on the dynamic behavior of multiple delaminated composite plates and shells. J Sound Vib 248:195–214. https://doi.org/10.1006/jsvi.2000.3506

    Article  Google Scholar 

  4. Khiloun M, Bousahla AA, Kaci A, Bessaim A, Tounsi A, Mahmoud SR (2019) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT. Eng Comput. https://doi.org/10.1007/s00366-019-00732-1

    Article  Google Scholar 

  5. Bourada F, Bousahla AA, Bourada B, Azzaz A, Zinata A, Tounsi A (2019) Dynamic investigation of porous functionally graded beam using a sinusoidal shear deformation theory. Wind Struct 28:19–30. https://doi.org/10.12989/was.2019.28.1.019

    Article  Google Scholar 

  6. Chaabane LA, Bourada F, Sekkal M et al (2019) Analytical study of bending and free vibration responses of functionally graded beams resting on elastic foundation. Struct Eng Mech 71:185–196. https://doi.org/10.12989/sem.2019.71.2.185

    Article  Google Scholar 

  7. Boukhlif Z, Bouremana B, Bourada F et al (2019) A simple quasi-3D HSDT for the dynamics analysis of FG thick plate on elastic foundation. Steel Compos Struct 31:503–516. https://doi.org/10.12989/scs.2019.31.5.503

    Article  Google Scholar 

  8. Boulefrakh L, Hebali H, Chikh A (2019) The effect of parameters of visco-Pasternak foundation on the bending and vibration properties of a thick FG plate. Geomech Eng 18:161–178. https://doi.org/10.12989/gae.2019.18.2.161

    Article  Google Scholar 

  9. Boutaleb S, Benrahou KH, Bakora A et al (2019) Dynamic Analysis of nanosize FG rectangular plates based on simple nonlocal quasi 3D HSDT. Adv Nano Res 7:189–206. https://doi.org/10.12989/anr.2019.7.3.191

    Article  Google Scholar 

  10. Meksi R, Benyoucef S, Mahmoudi A, Tounsi A, Bedia EAA, Mahmoud SR (2019) An analytical solution for bending, buckling and vibration responses of FGM sandwich plates. J Sandw Struct Mater 21:727–757. https://doi.org/10.1177/1099636217698443

    Article  Google Scholar 

  11. Zaoui FZ, Ouinas D, Tounsi A (2019) New 2D and quasi-3D shear deformation theories for free vibration of functionally graded plates on elastic foundations. Compos Part B 159:231–247. https://doi.org/10.1016/j.compositesb.2018.09.051

    Article  Google Scholar 

  12. Zarga D, Tounsi A, Bousahla AA, Bourada F, Mahmoud SR (2019) Thermomechanical bending study for functionally graded sandwich plates using a simple quasi-3D shear deformation theory. Steel Compos Struct 32:389–410. https://doi.org/10.12989/SCS.2019.32.3.389

    Article  Google Scholar 

  13. Hellal H, BouradaM Hebali H, Bourada F, Tounsi A, Bousahla AA, Mahmoud S (2019) Dynamic and stability analysis of functionally graded material sandwich plates in hygro-thermal environment using a simple higher shear deformation theory. J Sand Struct Mater. https://doi.org/10.1177/1099636219845841

    Article  Google Scholar 

  14. Attia A, Bousahla AA, Tounsi A, Mahmoud SR, Alwabli AS (2018) A refined four variable plate theory for thermoelastic analysis of FGM plates resting on variable elastic foundations. Struct Eng Mech 65:453–464. https://doi.org/10.12989/sem.2018.65.4.453

    Article  Google Scholar 

  15. Hamza-Cherif R, Meradjah M, Zidour M, Tounsi A, Belmahi S, Bensattalah T (2018) Vibration analysis of nano beam using differential transform method including thermal effect. J Nano Res 54:1–14. https://doi.org/10.4028/www.scientific.net/JNanoR.54.1

    Article  Google Scholar 

  16. Karami B, Janghorban M, Shahsavari D, Tounsi A (2018) A size-dependent quasi-3D model for wave dispersion analysis of FG nanoplates. Steel Comp Struct 28:99–110. https://doi.org/10.12989/scs.2018.28.1.099

    Article  Google Scholar 

  17. Menasria A, Bouhadra A, Tounsi A, Bousahla AA (2017) A new and simple HSDT for thermal stability analysis of FG sandwich plates. Steel Compos Struct 25:157–175. https://doi.org/10.12989/SCS.2017.25.2.157

    Article  Google Scholar 

  18. El-Haina F, Bakora A, Bousahla AA, Tounsi A (2017) A simple analytical approach for thermal buckling of thick functionally graded sandwich plates. Struct Eng Mech 63:585–595. https://doi.org/10.12989/SEM.2017.63.5.585

    Article  Google Scholar 

  19. Chikh A, Tounsi A, Hebali H, Mahmoud SR (2017) Thermal buckling analysis of cross-ply laminated plates using a simplified HSDT. Smart Struct Syst 19:289–297. https://doi.org/10.12989/SSS.2017.19.3.289

    Article  Google Scholar 

  20. Bousahla AA, Benyoucef S, Tounsi A, Mahmoud SR (2016) On thermal stability of plates with functionally graded coefficient of thermal expansion. Struct Eng Mech 60:313–335. https://doi.org/10.12989/sem.2016.60.2.313

    Article  Google Scholar 

  21. Fahsi A, Tounsi A, Hebali H, Chikh A, Bedia EAA, Mahmoud SR (2017) A four variable refined nth-order shear deformation theory for mechanical and thermal buckling analysis of functionally graded plates. Geomech Eng 13:385–410. https://doi.org/10.12989/gae.2017.13.3.385

    Article  Google Scholar 

  22. Hadi NH, Ameen KA (2011) Nonlinear free vibration of cylindrical shells with delamination using high order shear deformation theory-A finite element approach. Am J Sci Ind 2:251–277. https://doi.org/10.5251/ajsir.2011.2.2.251.277

    Article  Google Scholar 

  23. Dey S, Karmakar A (2012) Free vibration analysis of multiple delaminated angle-ply composite conical shells- a finite element approach. Compos Struct 94:2188–2196. https://doi.org/10.1016/j.compstruct.2012.01.006

    Article  Google Scholar 

  24. Hu N, Fukunaga H, Kameyama M, Aramaki Y, Chang FK (2002) Vibration analysis of delaminated composite beams and plates using a higher order finite elements. Int J Mater Sci 44:1479–1503. https://doi.org/10.1016/S0020-7403(02)00026-7

    Article  MATH  Google Scholar 

  25. Williams TO, Addessio FL (1998) A dynamic model for laminated plates with delamination. Int J Solids Struct 35:83–106. https://doi.org/10.1016/S0020-7683(97)00055-3

    Article  MATH  Google Scholar 

  26. Bruno D, Greco F, Lonetti P (2005) A 3D delamination modeling technique based on plate and interface theories for laminated structures. Eur J Mech Solids/A 24:127–149. https://doi.org/10.1016/j.euromechsol.2004.11.005

    Article  MATH  Google Scholar 

  27. Li S, Reid SR, Soden PD (1994) A finite strip analysis of cracked laminates. Mech Mater 18:289–311. https://doi.org/10.1016/0167-6636(94)90041-8

    Article  Google Scholar 

  28. Krueger R, O’Brien TK (2001) A shell/3D modeling technique for the analysis of delaminated composite laminates. Compos A 32:25–44. https://doi.org/10.1016/S1359-835X(00)00133-0

    Article  Google Scholar 

  29. Ramtekkar GS (2009) Free vibration analysis of delaminated beams using mixed finite element model. J Sound Vib 328:428–440. https://doi.org/10.1016/j.jsv.2009.08.008

    Article  Google Scholar 

  30. Lee F, Ju H, Lee KH (1995) Free vibration of composite plates with delaminations around cutouts. Compos Struct 32:177–183. https://doi.org/10.1016/0263-8223(95)00016-X

    Article  Google Scholar 

  31. Allix O, Ladeveze P (1992) Inter laminar interface modeling for the prediction of delamination. Compos Struct 22:235–242. https://doi.org/10.1016/0263-8223(92)90060-P

    Article  Google Scholar 

  32. Wang SS, Yu TP (2006) Nonlinear mechanics of delamination in fibre-composite laminates: asymptotic solutions and computational results. Compos Sci Tech 66:776–784. https://doi.org/10.1016/j.compscitech.2004.12.020

    Article  Google Scholar 

  33. Tenek LH, Henneke EG, Gunzburger MD (1993) Vibration of delaminated composite plates and some application to non-destructive testing. Compos Struct 23:253–262. https://doi.org/10.1016/0263-8223(93)90226-G

    Article  Google Scholar 

  34. Shu D, Della CN (2004) Vibration of multiple delaminated beams. Compos Struct 64:467–477. https://doi.org/10.1016/j.compstruct.2003.09.047

    Article  Google Scholar 

  35. Pipes RB, Vinson JR, Chou TW (1976) On the hygrothermal response of laminated composite systems. J Compos Mater 10:129–148. https://doi.org/10.1177/002199837601000203

    Article  Google Scholar 

  36. Kundu CK, Maiti DK, Sinha PK (2007) Nonlinear finite element analysis of laminated composite doubly curved shells in hygrothermal environment. J Reinf Plast Compos 26:1461–1478. https://doi.org/10.1177/0731684407079751

    Article  Google Scholar 

  37. Zine A, Tounsi A, Draiche K, Sekkal M, Mahmoud SR (2018) A novel higher-order shear deformation theory for bending and free vibration analysis of isotropic and multilayered plates and shells. Steel Compos Struct 26:125–137. https://doi.org/10.12989/scs.2018.26.2.125

    Article  Google Scholar 

  38. Karami B, Janghorbana M, Tounsi A (2018) Variational approach for wave dispersion in anisotropic doubly-curved nanoshells based on a new nonlocal strain gradient higher order shell theory. Thin-Walled Struct 129:251–264. https://doi.org/10.1016/j.tws.2018.02.025

    Article  Google Scholar 

  39. Sofiyev AH (2012) The nonlinear vibration of FGM truncated conical shells. Compos Struct 94:2237–2245. https://doi.org/10.1016/j.compstruct.2012.02.005

    Article  Google Scholar 

  40. Tripathi V, Singh BN, Shukla KK (2007) Free vibration of laminated composite conical shells with random material properties. Compos Struct 81:96–104. https://doi.org/10.1016/j.compstruct.2006.08.002

    Article  Google Scholar 

  41. Correia IFP, Barbosa JI, Soares CMM, Soares CAM (2000) A finite element semi-analytical model for laminated axis-symmetric shells: statics, dynamics and buckling. Comput Struct 76:299–317. https://doi.org/10.1016/S0045-7949(99)00165-0

    Article  Google Scholar 

  42. Reddy JN (1997) Mechanics of laminated composite plates—theory and analysis. CRC Press, London, Boca Raton

    MATH  Google Scholar 

  43. Lo SH, Zhen W, Cheung YK, Wanji C (2010) Hygrothermal effects on multilayered composite plates using a refined higher order theory. Compos Struct 92:633–646. https://doi.org/10.1016/j.compstruct.2009.09.034

    Article  Google Scholar 

  44. Faooq U, Gregory K (2009) Modeling and simulation of delamination in fibrous composite panels under low velocity impact from variable shape impactors. Europ J of Sci Res 25:614–635

    Google Scholar 

  45. Correia IFP, Soares CMM, Soares CAM, Hreskovits J (2003) Analysis of laminated conical shell structures using higher order models. Compos Struct 62:383–390. https://doi.org/10.1016/j.compstruct.2003.09.009

    Article  Google Scholar 

  46. Cook RD, Malkus DS, Plesha ME, Witt RJ (1989) Concepts and applications of finite element analysis. Wiley, Madison

    MATH  Google Scholar 

  47. Huebner KH, Dewhirst DL, Smith DE, Byrom TG (2001) The finite element method for engineers. Wiley, NewYork

    Google Scholar 

  48. Liew KM, Lim CW, Ong LS (1994) Vibration of pre-twisted cantilever shallow conical shells. Int J Solids Struct 31:2463–2474. https://doi.org/10.1016/0020-7683(94)90031-0

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Indian Space Research Organization, Vikram Sarabhai Space Centre, Trivandrum, India

    Achutananda Parhi

  2. Department of Aerospace Engineering, Indian Institute of Technology, Kharagpur, 208016, India

    B. N. Singh

  3. Department of Mechanical Engineering, National Institute of Technology, Rourkela, 769008, India

    Subrata K. Panda

Authors
  1. Achutananda Parhi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. B. N. Singh
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Subrata K. Panda
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Subrata K. Panda.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Parhi, A., Singh, B.N. & Panda, S.K. Nonlinear free vibration analysis of composite conical shell panel with cluster of delamination in hygrothermal environment. Engineering with Computers 37, 1565–1577 (2021). https://doi.org/10.1007/s00366-019-00903-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00903-0

Keywords