Skip to main content
SpringerLink
Log in

Statistical learning algorithm for concurrency of tensile strength tests

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

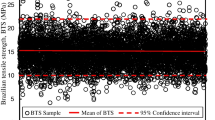
Direct and indirect test procedures are utilized to provide tensile strengths of rock and concrete samples. While the measurements provided by these methods are considered as identical in theory, a difference between the values is recorded in practice. To provide an association between the tensile test methods, a data-driven algorithm for identifying the uncertainty systems has been suggested. This study presents a novel algorithm including two steps: data processing-fusion and simulation. In the first step, both random and systematic error components in the tensile strength testing procedures are fused by uncertainty treatment-based data processing. By this way, instead of some assumptions and descriptive statistics, a data-fusion method is adapted. After that, a Monte Carlo simulation is performed using parametric and nonparametric probability distributions. Thus, a concurrency between the tensile strength procedures including strength values and uncertainty intervals is provided. The case study implemented by a real data set showed that the proposed algorithm has a feature of transparency, flexibility and also accuracy. The density functions used in the simulations do not require being normal while the conventional uncertainty-based data processing, Taylor’s ISO-GUM method depends on the normality. In addition, the algorithm does not need specification of coverage factor and it also works without any sensitivity coefficient. The methodology can be recommended to provide an agreement between the tensile strength values of rocks especially with limited number of data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Paterson MS, Wong T-F (2005) Experimental rock deformation—the brittle field, 2nd edn. Springer, Berlin

    Google Scholar 

  2. Perras MA, Diederichs MS (2014) A review of the tensile strength of rock: concepts and testing. Geotech Geol Eng 32:525–546

    Article  Google Scholar 

  3. Moss RES (2008) Quantifying measurement uncertainty of thirty meter shear wave velocity (VS30). Bull Seismol Soc Am 98(3):1399–1411

    Article  Google Scholar 

  4. Kuhinek D, Zoric I, Hrzenjak P (2011) Measurement uncertainty in testing of uniaxial compressive strength and deformability of rock samples. Meas Sci Rev 11(4):112–117

    Article  Google Scholar 

  5. Dhoska K, Tola S, Pramono A, Vozga I (2018) Evaluation of measurement uncertainty for determination the mechanical resistance of the brick samples by using uniaxial compressive strength test. Int J Metrol Qual Eng 9(12):1–5

    Google Scholar 

  6. Koepke A, Lafarge T, Possolo A, Toman B (2017) Consensus building for interlaboratory studies, key comparisons, and meta-analysis. Metrologia 54:S34–S62

    Article  Google Scholar 

  7. Lysiak-Pastuszak E (2004) Interlaboratory analytical performance studies; a way to estimate measurement uncertainty. Oceanologia 46(3):427–438

    Google Scholar 

  8. Rukhin AL (2009) Weighted means statistics in interlaboratory studies. Metrologia 46:323–331

    Article  Google Scholar 

  9. Wang CM, Iyer HK (2010) On multiple-method studies. Metrologia 47:642–645

    Article  Google Scholar 

  10. Da Silva RJNB, Ricardo JNB, Pennecchi FR, Hibbert DB, Kuselman I (2018) Tutorial and spreadsheets for Bayesian evaluation of risks of false decisions on conformity of a multicomponent material or object due to measurement uncertainty. Chemom Intell Lab Syst 182:109–116

    Article  Google Scholar 

  11. Petosic A, Djurek I, Suhanek M, Grubesa S (2019) Interlaboratory comparisons’ measurement uncertainty in the field of environmental noise. Measurement 148:106932

    Article  Google Scholar 

  12. Pendrill LR (2014) Using measurement uncertainty in decision-making and conformity assessment. Metrologia 51:S206–S218

    Article  Google Scholar 

  13. Erarslan N, Williams DJ (2012) Experimental, numerical and analytical studies on tensile strength of rocks. Int J Rock Mech Min Sci 49:21–30

    Article  Google Scholar 

  14. Tutmez B, Unver B (2017) Uncertainty-based analysis for agreement of tensile-strength measurement procedures. Geotech Test J 40:506–514

    Article  Google Scholar 

  15. Ghamgosar M, Erarslan N, Williams DJ (2017) Experimental investigation of fracture process zone in rocks damaged under cyclic loadings. Exp Mech 57:97–113

    Article  Google Scholar 

  16. Hudson JA, Harrison JP (2000) Engineering rock mechanics: an introduction to principles. Elsevier, Amsterdam

    Google Scholar 

  17. Brisevac Z, Kujundzic T, Cajic S (2015) Current cognition of rock tensile strength testing by Brazilian test. Min Geol Pet Eng Bull 30(2):101–114. https://doi.org/10.17794/rgn.2015.2.2

    Article  Google Scholar 

  18. ISRM (2007) Suggested methods for determining tensile strength of rock materials. In: Ulusay R, Hudson JA (eds) The complete ISRM suggested methods for rock characterization, testing and monitoring: 1974–2006. ISRM Turkish National Group, Ankara

    Google Scholar 

  19. Singh PK, Tripathy A, Kainthola A, Mahanta B, Singh B, Singh TN (2017) Indirect estimation of compressive and shear strength from simple index tests. Eng Comput 33:1–11

    Article  Google Scholar 

  20. Rabinovich SG (2017) Evaluating measurement accuracy. Springer, Switzerland

    Book  Google Scholar 

  21. JCGM 100 (2008) Evaluation of measurement data—guide to the expression of uncertainty in measurement, BIPM, Serres, France

  22. Shaw BD (2017) Uncertainty analysis of experimental data with R. CRC Press, Boca Raton

    Book  Google Scholar 

  23. Adachi K (2016) Matrix-based introduction to multivariate data analysis. Springer, Singapore

    Book  Google Scholar 

  24. Servin C, Ceberio M, Jaimes A, Tweedie C, Kreinovich V (2013) How to describe and propagate uncertainty when processing time series: metrological and computational challenges, with potential applications to environmental studies. In: Chen SM, Pedrycz W (eds) Time series analysis, modeling and applications: a computational intelligence perspective. Springer, Berlin, pp 279–299

    Chapter  Google Scholar 

  25. Servin C, Kreinovich V (2015) Propagation of interval and probabilistic uncertainty in cyberinfrastructure-related data processing and data fusion. Springer, Cham

    Book  Google Scholar 

  26. Unpingco J (2015) Python for probability, statistics, and machine learning. Springer, Cham

    MATH  Google Scholar 

  27. Efron B, Tibshirani RJ (1993) An introduction to the Bootstrap. Chapman and Hall, London

    Book  Google Scholar 

  28. Efron B (2011) The bootstrap and Markov-chain Monte Carlo. J Biopharm Stat 21:1052–1062

    Article  MathSciNet  Google Scholar 

  29. Gorski B, Conlon B, Ljunggren B (2007) Determination of the direct and indirect tensile strength on cores from borehole KFM01D, SKB Report—SKB P-07-76, Sweden

  30. Astrua M, Ichim D, Pennecchi F, Pisani M (2007) Statistical techniques for assessing the agreement between two instruments. Metrologia 44:385–392

    Article  Google Scholar 

  31. Efron B, Hastie T (2016) Computer age statistical inference. Cambridge University Press, Cambridge

    Book  Google Scholar 

  32. Charki A, Pavese F (2019) Data comparisons and uncertainty: a roadmap for gaining in competence and improving the reliability of results. Int J Metrol Qual Eng 10(1):1–10

    Article  Google Scholar 

  33. Coleman HW, Steele WG (2018) Experimentation, validation, and uncertainty analysis for engineers. Wiley, Chichester

    Book  Google Scholar 

Download references

Acknowledgements

The author extends the appreciation to Editor-in-Chief Professor Mark Shephard and anonymous reviewers for the constructive comments.

Author information

Authors and Affiliations

  1. School of Engineering, Inonu University, 44280, Malatya, Turkey

    Bulent Tutmez

Authors
  1. Bulent Tutmez
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bulent Tutmez.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tutmez, B. Statistical learning algorithm for concurrency of tensile strength tests. Engineering with Computers 37, 1781–1789 (2021). https://doi.org/10.1007/s00366-019-00911-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00911-0

Keywords

Search

Navigation