Skip to main content
Springer Nature Link
Log in

A high-performance four-node flat shell element with drilling degrees of freedom

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

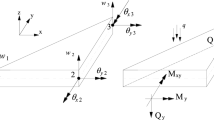
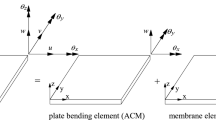
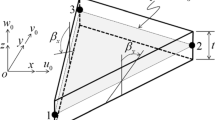
This paper presents a new four-node quadrilateral flat shell element, named QFSUQ, for analysis of shell structures. The element is formed by assemblage of a new membrane element and a plate-bending element. The membrane component is an unsymmetric quadrilateral element with drilling degrees of freedom. The trial functions of the membrane element are determined using the element stress fields formulated based on the analytical solutions of the Airy stress function in global Cartesian coordinate system. The corresponding test functions are obtained through the four-node isoparametric-based displacement fields which are enhanced by drilling rotations. The bending component is based on the Hellinger–Reissner variational principle for analysis of Reissner–Mindlin plates. To validate the performance of the proposed element several numerical benchmark problems are employed and the obtained results are compared with other shell elements. The results prove that the QFSUQ element preserves the advantages of the parent element formulation namely explicit stiffness matrix, free of membrane locking, shear locking and singularity problems and is also appropriate in analysis of shell structures with complex geometry, loading and boundary conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Nguyen-Hoang S, Phung-Van P, Natarajan S, Kim HG (2016) A combined scheme of edge-based and node-based smoothed finite element methods for Reissner–Mindlin flat shells. Eng Comput 32:267–284

    Google Scholar 

  2. Rezaiee-Pajand M, Arabi E, Masoodi AR (2018) A triangular shell element for geometrically nonlinear analysis. Acta Mech 229:323–342

    MathSciNet  MATH  Google Scholar 

  3. Tornabene F, Viola E (2013) Static analysis of functionally graded doubly-curved shells and panels of revolution. Meccanica 48:901–930

    MathSciNet  MATH  Google Scholar 

  4. Hernández E, Spa C, Surriba S (2018) A non-standard finite element method for dynamical behavior of cylindrical classical shell model. Meccanica 53:1037–1048

    MathSciNet  MATH  Google Scholar 

  5. Cheung YK, Zhang YX, Chen WJ (2000) A refined nonconforming plane quadrilateral element. Comput Struct 78:699–709

    Google Scholar 

  6. Cen S, Chen XM, Fu XR (2007) Quadrilateral membrane element family formulated by the quadrilateral area coordinate method. Comput Methods Appl Mech Eng 196:4337–4353

    MATH  Google Scholar 

  7. Chen J, Li CJ, Chen WJ (2010) A family of spline finite elements. Comput Struct 88:718–727

    Google Scholar 

  8. Zhang L, Bathe KJ (2017) Overlapping finite elements for a new paradigm of solution. Comput Struct 187:64–76

    Google Scholar 

  9. Rajendran S, Liew KM (2003) A novel unsymmetric 8-node plane element immune to mesh distortion under a quadratic displacement field. Int J Numer Meth Eng 58:1713–1748

    MATH  Google Scholar 

  10. Liew KM, Rajendran S, Wang J (2006) A quadratic plane triangular element immune to quadratic mesh distortions under quadratic displacement fields. Comput Methods Appl Mech Eng 195:1207–1223

    MATH  Google Scholar 

  11. Ooi ET, Rajendran S, Yeo JH (2008) Remedies to rotational frame dependence and interpolation failure of US-QUAD8 element. Commun Numer Methods Eng 24:1203–1217

    MathSciNet  MATH  Google Scholar 

  12. Cen S, Zhou GH, Fu XR (2012) A shape-free 8-node plane element unsymmetric analytical trial function method. Int J Numer Meth Eng 91:158–185

    MATH  Google Scholar 

  13. Zhou PL, Cen S, Huang JB, Li CF, Zhang Q (2017) An unsymmetric 8-node hexahedral element with high distortion tolerance. Int J Numer Meth Eng 109:1130–1158

    MathSciNet  Google Scholar 

  14. Xie Q, Sze KY, Zhou YX (2016) Modified and Trefftz unsymmetric finite element models. Int J Mech Mater Des 12:53–70

    Google Scholar 

  15. Shang Y, Ouyang W (2018) 4-Node unsymmetric quadrilateral membrane element with drilling DOFs insensitive to severe mesh-distortion. Int J Numer Meth Eng 113:1589–1606

    MathSciNet  Google Scholar 

  16. Shi G, Liu Y, Wang X (2015) Accurate, efficient, and robust Q4-like membrane elements formulated in Cartesian coordinates using the quasi-conforming element technique. Math Probl Eng 2015:198390

    MATH  Google Scholar 

  17. Wang C, Zhang X, Hu P (2016) New formulation of quasi-conforming method: a simple membrane element for analysis of planar problems. Eur J Mech A/Solids 60:122–133

    MathSciNet  MATH  Google Scholar 

  18. Allman DJ (1984) A compatible triangular element including vertex rotations for plane elasticity analysis. Comput Struct 19:1–8

    MATH  Google Scholar 

  19. Cook RD (1986) On the Allman triangle and a related quadrilateral element. Comput Struct 22:1065–1067

    Google Scholar 

  20. Groenwold AA, Xiao QZ, Theron NJ (2004) Accurate solution of traction free boundaries using hybrid stress membrane elements with drilling degrees of freedom. Comput Struct 82:2071–2081

    Google Scholar 

  21. Çalık Karaköse ÜH, Askes H (2010) Static and dynamic convergence studies of a four-noded membrane finite element with rotational degrees of freedom based on displacement superposition. Int J Numer Methods Biomed Eng 26:1263–1275

    MATH  Google Scholar 

  22. Zouari W, Hammadi F, Ayad R (2016) Quadrilateral membrane finite elements with rotational DOFs for the analysis of geometrically linear and nonlinear plane problems. Comput Struct 173:139–149

    Google Scholar 

  23. Batoz JL, Hammadi F, Zheng C, Zhong W (2000) On the linear analysis of plates and shells using a new-16 degrees of freedom flat shell element. Comput Struct 78:11–20

    Google Scholar 

  24. Batoz JL, Zheng CL, Hammadi F (2001) Formulation and evaluation of new triangular, quadrilateral, pentagonal and hexagonal discrete Kirchhoff plate/shell elements. Int J Numer Meth Eng 52:615–630

    MathSciNet  MATH  Google Scholar 

  25. Zengjie G, Wanji C (2003) Refined triangular discrete Mindlin flat shell elements. Comput Mech 33:52–60

    MATH  Google Scholar 

  26. Pimpinelli G (2004) An assumed strain quadrilateral element with drilling degrees of freedom. Finite Elem Anal Des 41:267–283

    Google Scholar 

  27. Sabourin F, Carbonniere J, Brunet M (2009) A new quadrilateral shell element using 16 degrees of freedom. Eng Comput 26:500–540

    MATH  Google Scholar 

  28. Wang Z, Sun Q (2014) Corotational nonlinear analyses of laminated shell structures using a 4-node quadrilateral flat shell element with drilling stiffness. Acta Mech Sin 30:418–429

    MathSciNet  MATH  Google Scholar 

  29. Hamadi D, Ayoub A, Abdelhafid O (2015) A new flat shell finite element for the linear analysis of thin shell structures. Eur J Comput Mech 24:232–255

    Google Scholar 

  30. Sangtarash H, Arab HG, Sohrabi MR, Ghasemi MR (2019) Formulation and evaluation of a new four-node quadrilateral element for analysis of the shell structures. Eng Comput. https://doi.org/10.1007/s00366-019-00763-8

    Article  Google Scholar 

  31. Shang Y, Cen S, Li CF (2016) A 4-node quadrilateral flat shell element formulated by the shape-free HDF plate and HSF membrane elements. Eng Comput 33:713–741

    Google Scholar 

  32. Huang M, Zhao Z, Shen C (2010) An effective planar triangular element with drilling rotation. Finite Elem Anal Des 46:1031–1036

    Google Scholar 

  33. Cen S, Fu XR, Zhou MJ (2011) 8-and 12-node plane hybrid stress-function elements immune to severely distorted mesh containing elements with concave shapes. Comput Methods Appl Mech Eng 200:2321–2336

    MathSciNet  MATH  Google Scholar 

  34. Tang LM, Liu YX (1985) Quasi-conforming element techniques for penalty finite element methods. Finite Elem Anal Des 1:25–33

    MATH  Google Scholar 

  35. Wang C, Zhang X, Hu P (2016) A 4-node quasi-conforming quadrilateral element for couple stress theory immune to distorted mesh. Comput Struct 175:52–64

    Google Scholar 

  36. Wang C, Wang X, Zhang X, Hu P (2017) Assumed stress quasi-conforming technique for static and free vibration analysis of Reissner–Mindlin plates. Int J Numer Meth Eng 112:303–337

    MathSciNet  Google Scholar 

  37. Cook RD, Malkus DS, Plesha ME, Witt RJ (1974) Concepts and applications of finite element analysis, vol 4. Wiley, New York

    Google Scholar 

  38. Taylor RL (1987) Finite element analysis of linear shell problems. In: Whiteman JR (ed) Proceedings of the mathematics in finite elements and applications, pp 191–203

  39. Ooi ET, Rajendran S, Yeo JH (2004) A 20-node hexahedron element with enhanced distortion tolerance. Int J Numer Meth Eng 60:2501–2530

    MATH  Google Scholar 

  40. Dvorkin EN, Bathe KJ (1984) A continuum mechanics based four-node shell element for general non-linear analysis. Eng Comput 1:77–88

    Google Scholar 

  41. Ko Y, Lee PS, Bathe KJ (2017) A new 4-node MITC element for analysis of two-dimensional solids and its formulation in a shell element. Comput Struct 192:34–49

    Google Scholar 

  42. ABAQUS (2012) Abaqus 6.12 Theory Manual. Dassault Systèmes Simulia Corp., Providence, Rhode Island

  43. Klinkel S, Gruttmann F, Wagner W (2006) A robust non-linear solid shell element based on a mixed variational formulation. Comput Methods Appl Mech Eng 195:179–201

    MATH  Google Scholar 

  44. Rezaiee-Pajand M, Yaghoobi M (2018) An efficient flat shell element. Meccanica 53:1015–1035

    MathSciNet  MATH  Google Scholar 

  45. Ibrahimbegović A, Frey F (1994) Stress resultant geometrically non-linear shell theory with drilling rotations. Part III: Linearized kinematic. Int J Numer Meth Eng 37:3659–3683

    MATH  Google Scholar 

  46. Belytschko T, Leviathan I (1994) Physical stabilization of the 4-node shell element with one point quadrature. Comput Methods Appl Mech Eng 113:321–350

    MATH  Google Scholar 

  47. Alves de Sousa RJ, Cardoso RP, Fontes Valente RA, Yoon JW, Grácio JJ, Natal Jorge RM (2005) A new one-point quadrature enhanced assumed strain (EAS) solid-shell element with multiple integration points along thickness: Part I—geometrically linear applications. Int J Numer Meth Eng 62:952–977

    MATH  Google Scholar 

  48. Hu P, Xia Y, Tang L (2011) A four-node Reissner–Mindlin shell with assumed displacement quasi-conforming method. Comput Model Eng Sci 73:103–135

    MATH  Google Scholar 

  49. Norachan P, Suthasupradit S, Kim KD (2012) A co-rotational 8-node degenerated thin-walled element with assumed natural strain and enhanced assumed strain. Finite Elem Anal Des 50:70–85

    MathSciNet  Google Scholar 

  50. Alves de Sousa RJ, Natal Jorge RM, Fontes Valente RA, César de Sá JMA (2003) A new volumetric and shear locking-free 3D enhanced strain element. Eng Comput 20:896–925

    MATH  Google Scholar 

  51. Abed-Meraim F, Combescure A (2007) A physically stabilized and locking-free formulation of the (SHB8PS) solid-shell element. Eur J Comput Mech/Revue Européenne de Mécanique Numérique 16:1037–1072

    MATH  Google Scholar 

  52. Nguyen-Thanh N, Rabczuk T, Nguyen-Xuan H, Bordas SP (2008) A smoothed finite element method for shell analysis. Comput Methods Appl Mech Eng 198:165–177

    MATH  Google Scholar 

  53. Moreira RAS, Rodrigues JD (2011) A non-conforming plate facet-shell finite element with drilling stiffness. Finite Elem Anal Des 47:973–981

    Google Scholar 

  54. Wang C, Hu P, Xia Y (2012) A 4-node quasi-conforming Reissner–Mindlin shell element by using Timoshenko's beam function. Finite Elem Anal Des 61:12–22

    MathSciNet  Google Scholar 

  55. Timoshenko SP, Woinowsky-Krieger S (1959) Theory of plates and shells. McGraw-hill, New York

    MATH  Google Scholar 

  56. Timoshenko S, Goodier JN (1979) Theory of elasticity, 3rd edn. McGraw-Hill, New York

    MATH  Google Scholar 

  57. Flügge W (1973) Stresses in shells. Springer-Verlag, New York

    MATH  Google Scholar 

  58. Macneal RH, Harder RL (1985) A proposed standard set of problems to test finite element accuracy. Finite Elem Anal Des 1:3–20

    Google Scholar 

  59. Simo JC, Fox DD, Rifai MS (1989) On a stress resultant geometrically exact shell model. Part II: the linear theory; computational aspects. Comput Methods Appl Mech Eng 73:53–92

    MATH  Google Scholar 

  60. Knight NF (1997) Raasch challenge for shell elements. AIAA J 35:375–381

    MATH  Google Scholar 

  61. Belytschko T, Stolarski H, Liu WK, Carpenter N, Ong JS (1985) Stress projection for membrane and shear locking in shell finite elements. Comput Methods Appl Mech Eng 51:221–258

    MathSciNet  MATH  Google Scholar 

  62. Lee PS, Bathe KJ (2002) On the asymptotic behavior of shell structures and the evaluation in finite element solutions. Comput Struct 80:235–255

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Civil Engineering Department, University of Sistan and Baluchestan, 98167-45845, Zahedan, Iran

    Hosein Sangtarash, Hamed G. Arab, Mohammad R. Sohrabi & Mohammad R. Ghasemi

Authors
  1. Hosein Sangtarash
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hamed G. Arab
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Mohammad R. Sohrabi
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Mohammad R. Ghasemi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hamed G. Arab.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sangtarash, H., Arab, H.G., Sohrabi, M.R. et al. A high-performance four-node flat shell element with drilling degrees of freedom. Engineering with Computers 37, 2837–2852 (2021). https://doi.org/10.1007/s00366-020-00974-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-00974-4

Keywords