Skip to main content
Springer Nature Link
Log in

SEREP-based reduced model of higher order viscoelastic propeller shaft considering various asymmetries

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

The material damping of rotors causes instability by introducing tangential force to whirl orbit. Literature shows that the improvement of stability range is achieved using fibre-reinforced composites or layered rotors which are light yet strong and exhibit better damping properties. In this study, a multi-layered viscoelastic propeller shaft mounted on three journal bearings is considered. Higher order finite-element model is developed after utilizing operator-based constitutive relationship, which includes various asymmetries from several sources like gyroscopic effect, internal damping, and journal bearing support. A large number of states of the higher order model, as well as the presence of asymmetry, make the system complicated for post-processing. Modified system equivalent reduction expansion process (SEREP) is applied for model reduction that uses both right and left eigenvectors of the original propeller-shaft system. Different numerical results are compared to test the effectiveness of reduced model. Though SEREP is found in the literature, its application over most realistic and higher order asymmetric system is completely new.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Bland DR (1960) The theory of linear viscoelasticity. Pergamon Press, Oxford

    MATH  Google Scholar 

  2. Zorzi ES, Nelson HD (1977) Finite element simulation of rotor—bearing systems with internal damping. J Eng Power Trans ASME 99:71–76. https://doi.org/10.1115/1.3446254

    Article  Google Scholar 

  3. Guran A, Rimrott FPJ, Janabi-Sharifi F (1991) On the stability of a spinning viscoelastic column. J Struct Mech 19(4):437–455. https://doi.org/10.1080/08905459108905151

    Article  Google Scholar 

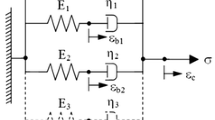
  4. Dutt JK, Roy H (2011) Viscoelastic modelling of rotor-shaft systems using an operator-based approach. J Mech Sci Inst Mech Eng Part C 225(1):73–87. https://doi.org/10.1243/09544062JMES2064

    Article  Google Scholar 

  5. Jivkov VS, Zahariev EV (2014) Stability and nonstationary vibrations of rotor in elastoviscous field. Mech Based Des Struct Mach 42(1):35–55. https://doi.org/10.1080/15397734.2013.814545

    Article  Google Scholar 

  6. Montagnier O, Hochard C (2014) Dynamics of a supercritical composite shaft mounted on viscoelastic supports. J Sound Vib 333:470–484. https://doi.org/10.1016/j.jsv.2013.09.021

    Article  Google Scholar 

  7. Roy H, Dutt JK (2016) Dynamics of polymer and polymer composite rotors—an operator based finite element approach. Appl Math Model 40:1754–1768. https://doi.org/10.1016/j.apm.2015.08.021

    Article  MathSciNet  MATH  Google Scholar 

  8. Roy H, Chandraker S, Dutt JK, Roy T (2016) Dynamics of multilayer, multidisc viscoelastic rotor—an operator based higher order classical model. J Sound Vib 369:87–108. https://doi.org/10.1016/j.jsv.2015.12.047

    Article  Google Scholar 

  9. Roy H, Chandraker S (2017) Dynamic study of viscoelastic rotor: modal analysis of higher order model considering various asymmetries. Mech Mach Theory 109:65–77. https://doi.org/10.1016/j.mechmachtheory.2016.11.003

    Article  Google Scholar 

  10. Guyan RJ (1965) Reduction of stiffness and mass matrices. Am Inst Aeronaut Astronaut 3(2):380–380. https://doi.org/10.2514/3.2874

    Article  Google Scholar 

  11. O'Callahan JC (1989) A procedure for an improved reduced system (IRS) model. In: Proceedings of the seventh international modal analysis conference, Las Vegas, pp 17–21

  12. Gordis JH (1992) An analysis of the improved reduced system (IRS) model reduction procedure. In: 10th international modal analysis conference, San Diego, vol 1(A94-12476 02-39), pp 471–479

  13. Friswell MI, Garvey SD, Penny JET (1998) The convergence of the iterated IRS methods. J Sound Vib 211(1):123–132. https://doi.org/10.1006/jsvi.1997.1368

    Article  MathSciNet  MATH  Google Scholar 

  14. Chandraker S, Roy H (2014) A balanced IIRS model for investigating the dynamics of damped rotor bearing system. In: Proceedings of the ASME gas turbine India conference V001T06A014. https://doi.org/10.1115/GTINDIA2014-8279

  15. Chandraker S, Roy H (2016) Dynamic study of viscoelastic rotor: reduction of higher order model using different techniques. Aerosp Sci Technol 58:306–317. https://doi.org/10.1016/j.ast.2016.08.006

    Article  Google Scholar 

  16. O'Callahan JC, Avitable P, Riemer R (1989) System equivalent reduction expansion process (SEREP). In: Proceedings of the seventh international modal analysis conference. Las Vegas, pp 29–37

  17. Friswell MI, Inman DJ (1999) Reduced-order models of structures with viscoelastic components. Am Inst Aeronaut Astronaut 37(10):1325–1328. https://doi.org/10.2514/2.603

    Article  Google Scholar 

  18. Friswell MI, Penny JET (1998) Garvey SD (2001) Model reduction for structures with damping and gyroscopic effects. Proc Int Semin Modal Anal KU Leuven 3:1151–1158

    Google Scholar 

  19. Das A, Dutt JK (2008) Reduced model of a rotor shaft system using modified SEREP. Mech Res Commun 35:398–407. https://doi.org/10.1016/j.mechrescom.2008.04.004

    Article  MATH  Google Scholar 

  20. Zhang Z, Zhang Z, Huang X, Hua H (2014) Stability and transient dynamics of a propeller-shaft system as induced by nonlinear friction acting on bearing-shaft contact interface. J Sound Vib 333(12):2608–2630. https://doi.org/10.1016/j.jsv.2014.01.026

    Article  Google Scholar 

  21. Meirovitch L (1975) Elements of vibration analysis. McGraw-Hill Science, Engineering & Mathematics, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology, Rourkela, Orissa, 769008, India

    Krishanu Ganguly & Haraprasad Roy

Authors
  1. Krishanu Ganguly
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Haraprasad Roy
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Haraprasad Roy.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ganguly, K., Roy, H. SEREP-based reduced model of higher order viscoelastic propeller shaft considering various asymmetries. Engineering with Computers 37, 3237–3249 (2021). https://doi.org/10.1007/s00366-020-00978-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-00978-0

Keywords

Profiles

  1. Krishanu Ganguly View author profile