Development of a shell superelement for large deformation and free vibration analysis of composite spherical shells

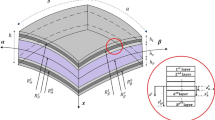
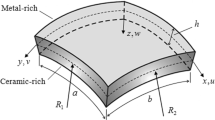
Abstract

Finite element analysis of huge and/or complicated structures often requires long times and large computational expenses. Superelements are huge elements that exploit the deformation theory of a specific problem to provide the capability of discretizing the problem with minimum number of elements. They are employed to reduce the computational cost while retaining the accuracy of results in FEM analysis of engineering problems. In this research, a new shell superelement is presented to study linear/nonlinear static and free vibration analysis of spherical structures with partial or full spherical geometries that exist in many industrial applications. Furthermore, this study investigates the effects of changing the superelement size and its number of nodes on solution accuracy. The governing equations of composite spherical shells are derived based on the first-order shear deformation theory and considering large deformations. For solving the nonlinear governing equations, the tangent stiffness matrix has been extracted and the Newton–Raphson method is employed. The capability of the presented shell superelement is investigated in several problems under linear/nonlinear static and free vibration analysis. The results acquired by the presented shell superelements are compared with available results in the literature and conventional shell elements in a commercial software. Results comparisons reveal high accuracy at a reduced computational cost in the superelement model.

Appendices

Appendix 1

$\left[ {B_{m} } \right],\left[ {B_{b} } \right],\left[ {B_{s} } \right]$ and $\left[ {B_{NL} } \right]$ are given as the following equations:

$$\begin{aligned} & \left[ {B_{m} } \right] \\ & \quad = \left[ {\begin{array}{*{20}l} {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }}} \hfill & 0 \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }}} \hfill & 0 \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill \\ {\frac{{\cot \left( \varphi \right)}}{R}N_{1} } \hfill & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {\frac{{\cot \left( \varphi \right)}}{R}N_{i} } \hfill & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} \hfill & {\frac{1}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill \\ {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} \hfill & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} \hfill & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{i} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] \\ & \left[ {B_{b} } \right] \\ & \quad = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }}} & 0 \\ 0 & 0 & 0 & {\frac{{\cot \left( \varphi \right)}}{R}N_{1} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} \\ 0 & 0 & 0 & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{1} } \\ \end{array} \begin{array}{*{20}c} \ldots & 0 & 0 & 0 & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }}} & 0 \\ \ldots & 0 & 0 & 0 & {\frac{{\cot \left( \varphi \right)}}{R}N_{i} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} \\ \ldots & 0 & 0 & 0 & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }} - \frac{{\cot \left( \varphi \right)}}{R}N_{i} } \\ \end{array} } \right] \\ & \left[ {B_{s} } \right] \\ & \quad = \left[ {\begin{array}{*{20}c} { - \frac{1}{R}N_{1} } & 0 & {\frac{1}{R}\frac{{\partial N_{1} }}{{\partial \varphi }}} & 1 & 0 \\ 0 & { - \frac{1}{R}N_{1} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{1} }}{{\partial \theta }}} & 0 & 1 \\ \end{array} \begin{array}{*{20}c} {~~~ \ldots } & { - \frac{1}{R}N_{i} } & 0 & {\frac{1}{R}\frac{{\partial N_{i} }}{{\partial \varphi }}} & 1 & 0 \\ {~~~ \ldots } & 0 & { - \frac{1}{R}N_{i} } & {\frac{1}{{R\sin \left( \varphi \right)}}\frac{{\partial N_{i} }}{{\partial \theta }}} & 0 & 1 \\ \end{array} } \right] \\ & \left[ {B_{{NL}} } \right] = \left[ {\begin{array}{*{20}c} {B_{{NL}}^{{\left( 1 \right)}} } \\ {B_{{NL}}^{{\left( 2 \right)}} } \\ {B_{{NL}}^{{\left( 3 \right)}} } \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}\left\{ U \right\}^{T} ~\left\{ {\tilde{d}_{1} } \right\}^{T} \left\{ {\tilde{d}_{1} } \right\}} \\ {\frac{1}{2}\left\{ U \right\}^{T} ~\left\{ {\tilde{d}_{2} } \right\}^{T} \left\{ {\tilde{d}_{2} } \right\}} \\ {~~~\frac{1}{2}\left\{ U \right\}^{T} ~\left\{ {\tilde{d}_{1} } \right\}^{T} \left\{ {\tilde{d}_{2} } \right\}~} \\ \end{array} } \right\} \\ & [B_{{NL}} ] = \left[ {\begin{array}{*{20}c} {\frac{1}{{2R^{2} }}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{{\partial \varphi }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{{npe}} }}{{\partial \varphi }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0} \right\}} \\ {\frac{1}{{2R^{2} \sin ^{2} \left( \varphi \right)}}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \theta }}w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{{npe}} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \theta }}w_{i} \quad 0\quad 0} \right\}} \\ {\frac{1}{{R^{2} \sin \left( \varphi \right)}}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{{npe}} }}{{\partial \theta }}\mathop \sum \limits_{{i = 1}}^{{npe}} \frac{{\partial N_{i} }}{{\partial \varphi }}w_{i} \quad 0\quad 0} \right\}.} \\ \end{array} } \right] \\ \end{aligned}$$

(23)

Appendix 2

$K_{1} ,K_{2} ,K_{3} , \ldots ,K_{10}$ are specified as the following equations:

$$\begin{aligned} K_{1} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{m} } \right]^{T} \left[ A \right]\left[ {B_{m} } \right]{\text{d}}A \\ K_{2} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{m} } \right]^{T} \left[ A \right]\left[ {B_{NL} } \right]{\text{d}}A \\ K_{3} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{m} } \right]^{T} \left[ B \right]\left[ {B_{b} } \right]{\text{d}}A \\ K_{4} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {\tilde{B}_{NL} } \right]^{T} \left[ A \right]\left[ {B_{m} } \right]{\text{d}}A \\ K_{5} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {\tilde{B}_{NL} } \right]^{T} \left[ A \right]\left[ {B_{NL} } \right]{\text{d}}A \\ K_{6} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {\tilde{B}_{NL} } \right]^{T} \left[ B \right]\left[ {B_{b} } \right]{\text{d}}A \\ K_{7} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{b} } \right]^{T} \left[ B \right]\left[ {B_{m} } \right] dA \\ K_{8} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{b} } \right]^{T} \left[ B \right]\left[ {B_{NL} } \right] dA \\ K_{9} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{b} } \right]^{T} \left[ D \right]\left[ {B_{b} } \right]{\text{d}}A \\ K_{10} & = \mathop {\iint }\limits_{{A^{e} }}^{{}} \left[ {B_{s} } \right]^{T} \left[ {A_{s} } \right]\left[ {B_{s} } \right]{\text{d}}A. \\ \end{aligned}$$

(24)

In the above equation, $\left[ {\tilde{B}_{NL} } \right]$ is written as:

$$\begin{aligned} & \left[ {\tilde{B}_{NL} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{B}_{NL}^{\left( 1 \right)} } \\ {\tilde{B}_{NL}^{\left( 2 \right)} } \\ {\tilde{B}_{NL}^{\left( 3 \right)} } \\ \end{array} } \right] \\ & \tilde{B}_{NL}^{\left( 1 \right)} = \frac{1}{{R^{2} }}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} \quad 0\quad 0\quad \cdots \quad \cdots 0\quad 0\quad \frac{{\partial N_{npe} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} \quad 0\quad 0} \right\} \\ & \tilde{B}_{NL}^{\left( 2 \right)} = \frac{1}{{R^{2} \sin^{2} \left( \varphi \right)}}\left\{ {0\quad 0\quad \frac{{\partial N_{1} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} \quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \frac{{\partial N_{npe} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} \quad 0\quad 0} \right\} \\ & \tilde{B}_{NL}^{\left( 3 \right)} = \frac{1}{{R^{2} \sin \left( \varphi \right)}}\left\{ {0\quad 0\quad \left( {\frac{{\partial N_{1} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} } \right) + \left( {\frac{{\partial N_{1} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} } \right)\quad 0\quad 0\quad \ldots \quad \ldots \quad 0\quad 0\quad \left( {\frac{{\partial N_{npe} }}{\partial \theta }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \varphi }w_{i} } \right) + \left( {\frac{{\partial N_{npe} }}{\partial \varphi }\mathop \sum \limits_{i = 1}^{npe} \frac{{\partial N_{i} }}{\partial \theta }w_{i} } \right)\quad 0\quad 0} \right\}. \\ \end{aligned}$$

(25)

Appendix 3

This research uses the Newton–Raphson algorithm for solving the nonlinear governing equation as follows:

$$\begin{aligned} & \left[ {K^{t} \left( {\left\{ U \right\}^{r} } \right)} \right]\left\{ {\Delta U} \right\} = \left\{ F \right\} - \left[ {K \left( {\left\{ U \right\}^{r} } \right)} \right] \left\{ U \right\}^{r} \\ & \left\{ U \right\}^{r + 1} \,= \left\{ U \right\}^{r} + \left\{ {\Delta U} \right\} \\ \end{aligned}$$

(26)

where $K^{t}$ is the tangent stiffness matrix which is expressed as follows:

$$(K_{ij}^{t} )^{r} = K_{ik,j}^{r} U_{k}^{r} + K_{ij}^{r}$$

(27)

where

$$\begin{aligned} & K_{{ik,j}}^{r} = \left( {K_{2} } \right)_{{ik,j}}^{r} + \left( {K_{4} } \right)_{{ik,j}}^{r} + \left( {K_{5} } \right)_{{ik,j}}^{r} + \left( {K_{6} } \right)_{{ik,j}}^{r} + \left( {K_{8} } \right)_{{ik,j}}^{r} \\ & \left( {K_{2} } \right)_{{ik,j}}^{r} = \left( {B_{m} } \right)_{{pi}} ~\left( A \right)_{{pq}} ~\left( {B_{{NL}} } \right)_{{qk,j}} \\ & \left( {K_{4} } \right)_{{ik,j}}^{r} = \left( {\tilde{B}_{{NL}} } \right)_{{pi,j}} ~\left( A \right)_{{pq}} ~\left( {B_{m} } \right)_{{qk,j}} \\ & \left( {K_{5} } \right)_{{ik,j}}^{r} = \left( {\tilde{B}_{{NL}} } \right)_{{pi,j}} ~~~\left( A \right)_{{pq}} ~~~\left( {B_{{NL}} } \right)_{{qk}}^{r} + \left( {\tilde{B}_{{NL}} } \right)_{{pi}}^{r} ~~~\left( A \right)_{{pq}} ~~~\left( {B_{{NL}} } \right)_{{qk,j}} \\ & \left( {K_{6} } \right)_{{ik,j}} = \left( {\tilde{B}_{{NL}} } \right)_{{pi,j}} ~~~\left( B \right)_{{pq}} ~~~\left( {B_{b} } \right)_{{qk}} \\ & \left( {K_{8} } \right)_{{ik,j}} = \left( {B_{b} } \right)_{{pi}} ~~~\left( B \right)_{{pq}} ~~~\left( {B_{{NL}} } \right)_{{q,jk}} \\ & \quad i,j,k = 1:dof \times npe;\quad p,q = 1,2,3. \\ \end{aligned}$$

(28)

Nonzero terms of $\left( {B_{NL} } \right)_{pi,j}$ and $\left( {\tilde{B}_{NL} } \right)_{pi,j}$ matrices are defined as the following equations:

$$\left( {B_{NL} } \right)_{pi,j} = \left\{ {\begin{array}{*{20}c} {\left[ {B_{NL} } \right]_{1i,j} } \\ {\left[ {B_{NL} } \right]_{2i,j} } \\ {\left[ {B_{NL} } \right]_{3i,j} } \\ \end{array} } \right\},\left( {\tilde{B}_{NL} } \right)_{pi,j} = \left\{ {\begin{array}{*{20}c} {\left[ {\tilde{B}_{NL} } \right]_{1i,j} } \\ {\left[ {\tilde{B}_{NL} } \right]_{2i,j} } \\ {\left[ {\tilde{B}_{NL} } \right]_{3i,j} } \\ \end{array} } \right\}$$

(29)

where

$$\begin{aligned} & \left[ {B_{NL} } \right]_{1i,j} = \left[ {\begin{array}{*{20}c} {B_{1NLj}^{11} } & {B_{1NLj}^{12} } & \cdots & {B_{1NLj}^{1l} } \\ {B_{1NLj}^{21} } & {B_{1NLj}^{22} } & \cdots & {B_{1NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {B_{1NLj}^{k1} } & {B_{1NLj}^{k2} } & \cdots & {B_{1NLj}^{kl} } \\ \end{array} } \right],\quad \left[ {\tilde{B}_{NL} } \right]_{1i,j}= \left[ {\begin{array}{*{20}c} {\tilde{B}_{1NLj}^{11} } & {\tilde{B}_{1NLj}^{12} } & \cdots & {\tilde{B}_{1NLj}^{1l} } \\ {\tilde{B}_{1NLj}^{21} } & {\tilde{B}_{1NLj}^{22} } & \cdots & {\tilde{B}_{1NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{B}_{1NLj}^{k1} } & {\tilde{B}_{1NLj}^{k2} } & \cdots & {\tilde{B}_{1NLj}^{kl} } \\ \end{array} } \right] \\ & \left[ {B_{NL} } \right]_{2i,j} = \left[ {\begin{array}{*{20}c} {B_{2NLj}^{11} } & {B_{2NLj}^{12} } & \ldots & {B_{2NLj}^{1l} } \\ {B_{2NLj}^{21} } & {B_{2NLj}^{22} } & \ldots & {B_{2NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {B_{2NLj}^{k1} } & {B_{2NLj}^{k2} } & \ldots & {B_{2NLj}^{kl} } \\ \end{array} } \right],\quad \left[ {\tilde{B}_{NL} } \right]_{2i,j} = \left[ {\begin{array}{*{20}c} {\tilde{B}_{2NLj}^{11} } & {\tilde{B}_{2NLj}^{12} } & \cdots & {\tilde{B}_{2NLj}^{1l} } \\ {\tilde{B}_{2NLj}^{21} } & {\tilde{B}_{2NLj}^{22} } & \cdots & {\tilde{B}_{2NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{B}_{2NLj}^{k1} } & {\tilde{B}_{2NLj}^{k2} } & \cdots & {\tilde{B}_{2NLj}^{kl} } \\ \end{array} } \right] \\ & \left[ {B_{NL} } \right]_{3i,j} = \left[ {\begin{array}{*{20}c} {B_{3NLj}^{11} } & {B_{3NLj}^{12} } & \ldots & {B_{3NLj}^{1l} } \\ {B_{3NLj}^{21} } & {B_{3NLj}^{22} } & \ldots & {B_{3NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {B_{3NLj}^{k1} } & {B_{3NLj}^{k2} } & \ldots & {B_{3Lj}^{kl} } \\ \end{array} } \right] ,\quad \left[ {\tilde{B}_{NL} } \right]_{3i,j} = \left[ {\begin{array}{*{20}c} {\tilde{B}_{3NLj}^{11} } & {\tilde{B}_{3NLj}^{12} } & \cdots & {\tilde{B}_{3NLj}^{1l} } \\ {\tilde{B}_{3NLj}^{21} } & {\tilde{B}_{3NLj}^{22} } & \cdots & {\tilde{B}_{3NLj}^{1l} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{B}_{3NLj}^{k1} } & {\tilde{B}_{3NLj}^{k2} } & \cdots & {\tilde{B}_{3NLj}^{kl} } \\ \end{array} } \right] \\ & B_{1NLJ}^{kl} = \frac{1}{{2R^{2} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\varphi } N_{l,\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \tilde{B}_{1NLJ}^{kl} = \frac{1}{{R^{2} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\varphi } N_{l,\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & B_{2NLJ}^{kl} = \frac{1}{{2R^{2} \sin^{2} \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\theta } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \tilde{B}_{2NLJ}^{kl} = \frac{1}{{R^{2} \sin^{2} \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\theta } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & B_{3NLJ}^{kl} = \frac{1}{{R^{2} \sin \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \tilde{B}_{3NLJ}^{kl} = \frac{1}{{R^{2} \sin \left( \varphi \right)}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{k,\theta } N_{l,\varphi } + N_{k,\varphi } N_{l,\theta } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]. \\ \end{aligned}$$

(30)

Appendix 4

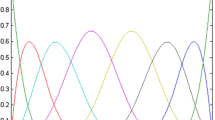
Shape functions of the spherical shell superelement including pole in the local coordinate system are expressed as follows:

• (a) $M = 3, N = 16$:

  $$\begin{gathered} \begin{array}{*{20}c} {N_{i} = \frac{{\gamma \left( {\gamma - 1} \right)}}{2}} & {i = 1} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {N_{{2,i}} = \frac{{\left( {1 - \gamma } \right)\left( {1 + \gamma } \right)}}{4} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {i = 1 - 16} \hfill \\ {\quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right]} \hfill & {} \hfill \\ \end{array} \hfill \\ \begin{array}{*{20}l} {N_{{3,i}} = \frac{{\gamma \left( {\gamma + 1} \right)}}{8} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {i = 1 - 16} \hfill \\ {\quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right]} \hfill & {} \hfill \\ \end{array} \hfill \\ \end{gathered}$$

  (31)

• (b) $M = 2, N = 16$:

  $$\begin{gathered} \begin{array}{*{20}c} {N_{i} = \frac{{\left( {1 - \lambda } \right)}}{2}} & {i = 1} \\ \end{array} \hfill \\ \begin{array}{*{20}l} {N_{{2,i}} = \frac{{\left( {1 + \lambda } \right)}}{{16}} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {i = 1 - 16} \hfill \\ {\quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right]} \hfill & {} \hfill \\ {\quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right]} \hfill & {} \hfill \\ \end{array} \hfill \\ \end{gathered}$$

  (32)

Also, the shape functions of the spherical shell superelement without pole are given as follows:

• (a) $M = 3, N = 16$:

  $$\begin{array}{*{20}l} \begin{aligned} & N_{{1,{\text{i}}}} = \frac{{\gamma \left( {\gamma - 1} \right)}}{8} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \begin{aligned} & N_{{2,{\text{i}}}} = \frac{{\left( {1 - \gamma } \right)\left( {1 + \gamma } \right)}}{4} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \begin{aligned} & N_{{3,{\text{i}}}} = \frac{{\gamma \left( {\gamma + 1} \right)}}{8} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \end{array}$$

  (33)

• (b) $M = 2, N = 16$:

  $$\begin{array}{*{20}l} \begin{aligned} & N_{{1,{\text{i}}}} = \frac{{\left( {1 - \lambda } \right)}}{{16}} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16} \hfill \\ \begin{aligned} & N_{{2,{\text{i}}}} = \frac{{\left( {1 + \lambda } \right)}}{{16}} \times \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right) \\ & \quad \times \left[ {1 + \cos \left( {4\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {2\left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right)} \right] \\ & \quad \times \left[ {1 + \cos \left( {\pi ~\left( {\mu + 1} \right) - \frac{{\left( {i - 1} \right) \times \pi }}{8}} \right)} \right] \\ \end{aligned} \hfill & {i = 1 - 16~} \hfill \\ \end{array} .$$

  (34)