Skip to main content
Springer Nature Link
Log in

Application of shifted Chebyshev polynomial-based Rayleigh–Ritz method and Navier’s technique for vibration analysis of a functionally graded porous beam embedded in Kerr foundation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

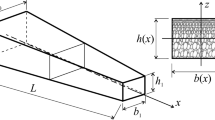
The present study is dealt with the applicability of shifted Chebyshev polynomial-based Rayleigh–Ritz method and Navier’s technique on free vibration of functionally graded (FG) beam with uniformly distributed porosity along the thickness of the beam. The material properties such as Young’s modulus, mass density, and Poisson’s ratio are also considered to vary along the thickness of the FG beam as per the power-law exponent model. The porous FG beam is embedded in an elastic substrate; namely, the Kerr elastic foundation and the displacement field of the beam are governed by a refined higher-order shear deformation theory. The effectiveness of the Rayleigh–Ritz method is due to the use of the shifted Chebyshev polynomials as a shape function. The orthogonality of shifted Chebyshev polynomial makes the technique more computationally efficient and avoid ill-conditioning for the higher number of terms of the polynomial. Hinged–hinged, clamped–hinged, clamped–clamped, and clamped-free boundary conditions have been taken into account for the parametric study. Validation of the present model is examined by comparing it with the existing literature in special cases showing remarkable agreement. A pointwise convergence study is also carried out for shifted Chebyshev polynomial-based Rayleigh–Ritz method, and the effect of power-law exponent, porosity volume fraction index, and elastic foundation on natural frequencies is studied comprehensively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Sina SA, Navazi HM, Haddadpour H (2009) An analytical method for free vibration analysis of functionally graded beams. Mater Des 30:741–747

    Google Scholar 

  2. Ke LL, Yang J, Kitipornchai S (2010) An analytical study on the nonlinear vibration of functionally graded beams. Meccanica 45:743–752

    MathSciNet  MATH  Google Scholar 

  3. Hein H, Feklistova L (2011) Free vibrations of non-uniform and axially functionally graded beams using Haar wavelets. Eng Struct 33:3696–3701

    Google Scholar 

  4. Shooshtari A, Rafiee M (2011) Nonlinear forced vibration analysis of clamped functionally graded beams. Acta Mech 221:23–38

    MATH  Google Scholar 

  5. Wattanasakulpong N, Prusty BG, Kelly DW (2011) Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int J Mech Sci 53:734–743

    Google Scholar 

  6. Wattanasakulpong N, Prusty BG, Kelly DW, Hoffman M (2012) Free vibration analysis of layered functionally graded beams with experimental validation. Mater Des 36:182–190

    Google Scholar 

  7. Thai HT, Vo TP (2012) Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int J Mech Sci 62:57–66

    Google Scholar 

  8. Fallah A, Aghdam MM (2012) Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Compos Part B 43:1523–1530

    Google Scholar 

  9. Pradhan KK, Chakraverty S (2013) Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh–Ritz method. Compos Part B 51:175–184

    Google Scholar 

  10. Rahimi GH, Gazor MS, Hemmatnezhad M, Toorani H (2013) On the post buckling and free vibrations of FG Timoshenko beams. Compos Struct 95:247–253

    Google Scholar 

  11. Vo TP, Thai HT, Nguyen TK, Maheri A, Lee J (2014) Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Eng Struct 64:12–22

    Google Scholar 

  12. Kanani AS, Niknam H, Ohadi AR, Aghdam MM (2014) Effect of nonlinear elastic foundation on large amplitude free and forced vibration of functionally graded beam. Compos Struct 115:60–68

    Google Scholar 

  13. Nguyen TK, Nguyen TTP, Vo TP, Thai HT (2015) Vibration and buckling analysis of functionally graded sandwich beams by a new higher-order shear deformation theory. Compos Part B Eng 76:273–285

    Google Scholar 

  14. Su H, Banerjee JR (2015) Development of dynamic stiffness method for free vibration of functionally graded Timoshenko beams. Comput Struct 147:107–116

    Google Scholar 

  15. Tossapanon P, Wattanasakulpong N (2016) Stability and free vibration of functionally graded sandwich beams resting on two-parameter elastic foundation. Compos Struct 142:215–225

    Google Scholar 

  16. Huang Y, Zhang M, Rong H (2016) Buckling analysis of axially functionally graded and non-uniform beams based on Timoshenko theory. Acta Mech Solida Sin 29:200–207

    Google Scholar 

  17. Chen D, Yang J, Kitipornchai S (2016) Free and forced vibrations of shear deformable functionally graded porous beams. Int J Mech Sci 108–109:14–22

    Google Scholar 

  18. Jing LL, Ming PJ, Zhang WP, Fu LR, Cao YP (2016) Static and free vibration analysis of functionally graded beams by combination Timoshenko theory and finite volume method. Compos Struct 138:192–213

    Google Scholar 

  19. Sedighi HM, Shirazi KH, Attarzadeh MA (2013) A study on the quintic nonlinear beam vibrations using asymptotic approximate approaches. Acta Astronaut 91:245–250

    Google Scholar 

  20. Sedighi HM, Shirazi KH, Noghrehabadi A (2012) Application of recent powerful analytical approaches on the non-linear vibration of cantilever beams. Int J Nonlinear Sci Numer Simul 13(7–8):487–494

    MathSciNet  MATH  Google Scholar 

  21. Sedighi HM, Daneshmand F (2014) Nonlinear transversely vibrating beams by the homotopy perturbation method with an auxiliary term. J Appl Comput Mech 1(1):1–9

    Google Scholar 

  22. Esmaeili M, Tadi Beni Y (2019) Vibration and buckling analysis of functionally graded flexoelectric smart beam. J Appl Comput Mech 5(5):900–917

    Google Scholar 

  23. Karami B, Janghorban M, Rabczuk T (2020) Dynamics of two-dimensional functionally graded tapered Timoshenko nanobeam in thermal environment using nonlocal strain gradient theory. Compos Part B Eng 182:107622

    Google Scholar 

  24. Karami B, Janghorban M, Li L (2018) On guided wave propagation in fully clamped porous functionally graded nanoplates. Acta Astronaut 143:380–390

    Google Scholar 

  25. She GL, Yuan FG, Karami B, Ren YR, Xiao WS (2019) On nonlinear bending behavior of FG porous curved nanotubes. Int J Eng Sci 135:58–74

    MathSciNet  MATH  Google Scholar 

  26. She GL, Jiang XY, Karami B (2019) On thermal snap-buckling of FG curved nanobeams. Mater Res Express 6(11):115008

    Google Scholar 

  27. Karami B, Shahsavari D, Janghorban M, Li L (2020) Free vibration analysis of FG nanoplate with poriferous imperfection in hygrothermal environment. Struct Eng Mech 73(2):191

    Google Scholar 

  28. Karami B, Shahsavari D, Janghorban M, Li L (2019) On the resonance of functionally graded nanoplates using bi-Helmholtz nonlocal strain gradient theory. Int J Eng Sci 144:103143

    MathSciNet  MATH  Google Scholar 

  29. Karami B, Shahsavari D, Li L (2018) Temperature-dependent flexural wave propagation in nanoplate-type porous heterogenous material subjected to in-plane magnetic field. J Therm Stress 41(4):483–499

    Google Scholar 

  30. Karami B, Janghorban M (2019) On the dynamics of porous nanotubes with variable material properties and variable thickness. Int J Eng Sci 136:53–66

    MathSciNet  MATH  Google Scholar 

  31. Alimirzaei S, Mohammadimehr M, Tounsi A (2019) Nonlinear analysis of viscoelastic micro-composite beam with geometrical imperfection using FEM: MSGT electro-magneto-elastic bending, buckling and vibration solutions. Struct Eng Mech 71(5):485–502

    Google Scholar 

  32. Karami B, Janghorban M, Tounsi A (2019) Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Eng Comput 35(4):1297–1316

    Google Scholar 

  33. Tounsi A, Al-Dulaijan SU, Al-Osta MA, Chikh A, Al-Zahrani MM, Sharif A, Tounsi A (2020) A four variable trigonometric integral plate theory for hygro-thermo-mechanical bending analysis of AFG ceramic-metal plates resting on a two-parameter elastic foundation. Steel Compos Struct 34(4):511–524

    Google Scholar 

  34. Addou FY, Meradjah M, Bousahla AA, Benachour A, Bourada F, Tounsi A, Mahmoud SR (2019) Influences of porosity on dynamic response of FG plates resting on Winkler/Pasternak/ Kerr foundation using quasi 3D HSDT. Comput Concr 24(4):347–367

    Google Scholar 

  35. Chaabane LA, Bourada F, Sekkal M, Zerouati S, Zaoui FZ, Tounsi A, Derras A, Bousahla AA, Tounsi A (2019) Analytical study of bending and free vibration responses of functionally graded beams resting on elastic foundation. Struct Eng Mech 71(2):185–196

    Google Scholar 

  36. Boukhlif Z, Bouremana M, Bourada F, Bousahla AA, Bourada M, Tounsi A, Al-Osta MA (2019) A simple quasi-3D HSDT for the dynamics analysis of FG thick plate on elastic foundation. Steel Compos Struct 31(5):503–516

    Google Scholar 

  37. Boulefrakh L, Hebali H, Chikh A, Bousahla AA, Tounsi A, Mahmoud SR (2019) The effect of parameters of visco-Pasternak foundation on the bending and vibration properties of a thick FG plate. Geomech Eng 18(2):161–178

    Google Scholar 

  38. Kaddari M, Kaci A, Bousahla AA, Tounsi A, Bourada F, Bedia EA, Al-Osta MA (2020) A study on the structural behaviour of functionally graded porous plates on elastic foundation using a new quasi-3D model: bending and free vibration analysis. Comput Concr 25(1):37

    Google Scholar 

  39. Bourada F, Bousahla AA, Bourada M, Azzaz A, Zinata A, Tounsi A (2019) Dynamic investigation of porous functionally graded beam using a sinusoidal shear deformation theory. Wind Struct 28(1):19–30

    Google Scholar 

  40. Khiloun M, Bousahla AA, Kaci A, Bessaim A, Tounsi A, Mahmoud SR (2019) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT. Eng Comput. https://doi.org/10.1007/s00366-019-00732-1

    Article  Google Scholar 

  41. Bousahla AA, Bourada F, Mahmoud SR, Tounsi A, Algarni A, Bedia EA, Tounsi A (2020) Buckling and dynamic behavior of the simply supported CNT-RC beams using an integral-first shear deformation theory. Comput Concr 25(2):155

    Google Scholar 

  42. Boussoula A, Boucham B, Bourada M, Bourada F, Tounsi A, Bousahla AA, Tounsi A (2020) A simple nth-order shear deformation theory for thermomechanical bending analysis of different configurations of FG sandwich plates. Smart Struct Syst 25(2):197

    Google Scholar 

  43. Paul A, Das D (2016) Free vibration analysis of pre-stressed FGM Timoshenko beams under large transverse deflection by a variational method. Eng Sci Technol 19:1003–1017

    Google Scholar 

  44. Wang X, Shirong L (2016) Free vibration analysis of functionally graded material beams based on Levinson beam theory. Appl Math Mech 37:861–878

    MathSciNet  MATH  Google Scholar 

  45. Kahya V, Turan M (2017) Finite element model for vibration and buckling of functionally graded beams based on the first-order shear deformation theory. Compos Part B 109:108–115

    Google Scholar 

  46. Nguyen DK, Nguyen QH, Tran TT, Bui VT (2017) Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech 228:141–155

    MathSciNet  MATH  Google Scholar 

  47. Deng H, Chen KD, Cheng W, Zhao SG (2017) Vibration and buckling analysis of double-functionally graded Timoshenko beam system on Winkler–Pasternak elastic foundation. Compos Struct 160:152–168

    Google Scholar 

  48. Celebi K, Yarimpabuc D, Tutuncu N (2018) Free vibration analysis of functionally graded beams using complementary functions method. Arch Appl Mech 88:729–739

    Google Scholar 

  49. Sinir S, Çevik M, Sinir BG (2018) Nonlinear free and forced vibration analyses of axially functionally graded Euler–Bernoulli beams with non-uniform cross-section. Compos Part B Eng 148:123–131

    Google Scholar 

  50. Banerjee JR, Ananthapuvirajah A (2018) Free vibration of functionally graded beams and frameworks using the dynamic stiffness method. J Sound Vib 422:34–47

    Google Scholar 

  51. Karamanli A (2018) Free vibration analysis of two directional functionally graded beams using a third order shear deformation theory. Compos Struct 189:127–136

    Google Scholar 

  52. Fazzolari FA (2018) Generalized exponential, polynomial and trigonometric theories for vibration and stability analysis of porous FG sandwich beams resting on elastic foundations. Compos Part B Eng 136:254–271

    Google Scholar 

  53. Cao D, Gao Y (2019) Free vibration of non-uniform axially functionally graded beams using the asymptotic development method. Appl Math Mech 40:85–96

    MathSciNet  Google Scholar 

  54. Wattanasakulpong N, Ungbhakorn V (2014) Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp Sci Technol 32(1):111–120

    Google Scholar 

  55. Shahsavari D, Shahsavari M, Li L, Karami B (2018) A novel quasi-3D hyperbolic theory for free vibration of FG plates with porosities resting on Winkler/Pasternak/Kerr foundation. Aerosp Sci Technol 72:134–149

    Google Scholar 

  56. Malikan M, Tornabene F, Dimitri R (2018) Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater Res Express 5(9):095006

    Google Scholar 

  57. Senthilnathan NR, Lim SP, Lee KH, Chow ST (1987) Buckling of shear-deformable plates. AIAA J 25(9):1268–1271

    Google Scholar 

  58. Bekhadda A, Bensaid I, Cheikh A, Kerboua B (2019) Static buckling and vibration analysis of continuously graded ceramic-metal beams using a refined higher-order shear deformation theory. Multidiscip Model Mater Struct. https://doi.org/10.1108/MMMS-03-2019-0057

    Article  Google Scholar 

  59. Daikh AA (2019) Temperature dependent vibration analysis of functionally graded sandwich plates resting on Winkler/Pasternak/Kerr foundation. Mater Res Express 6(6):065702

    Google Scholar 

  60. Jena SK, Chakraverty S, Malikan M (2020) Implementation of non-probabilistic methods for stability analysis of nonlocal beam with structural uncertainties. Eng Comput. https://doi.org/10.1007/s00366-020-00987-z

    Article  Google Scholar 

  61. Jena SK, Chakraverty S, Malikan M, Tornabene F (2019) Stability analysis of single-walled carbon nanotubes embedded in Winkler foundation placed in a thermal environment considering the surface effect using a new refined beam theory. Mech Des Struct Mach. https://doi.org/10.1080/15397734.2019.1698437

    Article  Google Scholar 

  62. Jena SK, Chakraverty S, Malikan M (2019) Vibration and buckling characteristics of nonlocal beam placed in a magnetic field embedded in Winkler–Pasternak elastic foundation using a new refined beam theory: an analytical approach. Eur Phys J Plus 135:1–18

    Google Scholar 

  63. Jena SK, Chakraverty S, Tornabene F (2019) Buckling behavior of nanobeam placed in an electro-magnetic field using shifted Chebyshev polynomials based Rayleigh–Ritz method. Nanomaterials 9(9):1326

    Google Scholar 

  64. Malikan M, Eremeyev VA (2020) Post-critical buckling of truncated conical carbon nanotubes considering surface effects embedding in a nonlinear Winkler substrate using the Rayleigh–Ritz method. Mater Res Express 7:025005

    Google Scholar 

  65. Jena SK, Chakraverty S, Jena RM (2019) Propagation of uncertainty in free vibration of Euler–Bernoulli nanobeam. J Braz Soc Mech Sci Eng 41(10):436

    Google Scholar 

  66. Yang J, Shen HS (2002) Vibration characteristics and transient response of shear-deformable functionally graded plates in thermal environments. J Sound Vib 255(3):579–602

    Google Scholar 

  67. Reddy JN, Chin CD (1998) Thermomechanical analysis of functionally graded cylinders and plates. J Therm Stress 21(6):593–626

    Google Scholar 

  68. Şimşek M (2010) Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nucl Eng Des 240(4):697–705

    MathSciNet  Google Scholar 

Download references

Acknowledgements

The first two authors would like to acknowledge Defence Research and Development Organization (DRDO), New Delhi, India (Sanction Code: DG/TM/ERIPR/GIA/17-18/0129/020), for the funding to carry out the present research work.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Rourkela, Rourkela, Odisha, 769008, India

    Subrat Kumar Jena & S. Chakraverty

  2. Department of Mechanics of Materials and Structures, Faculty of Civil and Environmental Engineering, Gdansk University of Technology, ul. G. Narutowicza 11/12, 80-233, Gdańsk, Poland

    Mohammad Malikan

Authors
  1. Subrat Kumar Jena
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Chakraverty
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Mohammad Malikan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. Chakraverty.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jena, S.K., Chakraverty, S. & Malikan, M. Application of shifted Chebyshev polynomial-based Rayleigh–Ritz method and Navier’s technique for vibration analysis of a functionally graded porous beam embedded in Kerr foundation. Engineering with Computers 37, 3569–3589 (2021). https://doi.org/10.1007/s00366-020-01018-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01018-7

Keywords