Skip to main content
Springer Nature Link
Log in

A parametric knot adaptation approach to isogeometric analysis of contact problems

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

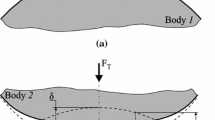
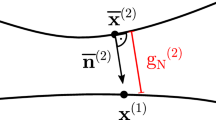
In this paper, an adaptive approach is presented to deal with isogeometric analysis of contact problems. Suggestion of an isogeometric adaptive refinement strategy for contact problems is the subject of this paper. Refinements are performed near the boundaries of the contact zone with insertion of new knots in the parametric domain. The performance and efficiency of the method are demonstrated via four examples, i.e., the Hertz problem and three hyperelastic contact problems. The obtained results are compared with solutions of very fine computational models. The proposed approach shows good convergence not only for the contact pressure but also for the contact zone limits. Another advantage of the method is eliminating the need for a priori guess of the contact zone limits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Franke D, Düster A, Nübel V, Rank E (2010) A comparison of the h-, p-, hp-, and rp-version of the FEM for the solution of the 2D Hertzian contact problem. Comput Mech 45(5):513–522

    Article  Google Scholar 

  2. Kagan P, Fischer A, Bar-Yoseph PZ (1998) New B-spline finite element approach for geometrical design and mechanical analysis. Int J Numer Methods Eng 41(3):435–458

    Article  Google Scholar 

  3. Gardner L, Gardner G, Dag I (1995) AB-spline finite element method for the regularized long wave equation. Commun Numer Methods Eng 11(1):59–68

    Article  Google Scholar 

  4. Braibant V, Fleury C (1984) Shape optimal design using B-splines. Comput Methods Appl Mech Eng 44(3):247–267

    Article  Google Scholar 

  5. Hughes TJ, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194(39–41):4135–4195

    Article  MathSciNet  Google Scholar 

  6. Borden MJ, Scott MA, Evans JA, Hughes TJ (2011) Isogeometric finite element data structures based on Bézier extraction of NURBS. Int J Numer Meth Eng 87(1–5):15–47

    Article  Google Scholar 

  7. Nguyen VP, Anitescu C, Bordas SP, Rabczuk T (2015) Isogeometric analysis: an overview and computer implementation aspects. Math Comput Simul 117:89–116

    Article  MathSciNet  Google Scholar 

  8. Temizer I, Wriggers P, Hughes T (2011) Contact treatment in isogeometric analysis with NURBS. Comput Methods Appl Mech Eng 200(9–12):1100–1112

    Article  MathSciNet  Google Scholar 

  9. Lu J (2011) Isogeometric contact analysis: geometric basis and formulation for frictionless contact. Comput Methods Appl Mech Eng 200(5–8):726–741

    Article  MathSciNet  Google Scholar 

  10. De Lorenzis L, Temizer I, Wriggers P, Zavarise G (2011) A large deformation frictional contact formulation using NURBS-based isogeometric analysis. Int J Numer Meth Eng 87(13):1278–1300

    Article  MathSciNet  Google Scholar 

  11. Dimitri R, De Lorenzis L, Scott M, Wriggers P, Taylor R, Zavarise G (2014) Isogeometric large deformation frictionless contact using T-splines. Comput Methods Appl Mech Eng 269:394–414

    Article  MathSciNet  Google Scholar 

  12. Belgacem FB, Hild P, Laborde P (1998) The mortar finite element method for contact problems. Math Comput Model 28(4):263–272

    Article  MathSciNet  Google Scholar 

  13. Kim JY, Youn SK (2012) Isogeometric contact analysis using mortar method. Int J Numer Methods Eng 89(12):1559–1581

    Article  MathSciNet  Google Scholar 

  14. De Lorenzis L, Wriggers P, Zavarise G (2017) A mortar formulation for 3D large deformation contact using NURBS-based isogeometric analysis and the augmented Lagrangian method. Comput Mech 49(1):1011–1031

    MathSciNet  MATH  Google Scholar 

  15. Zimmermann C, Sauer RA (2012) Adaptive local surface refinement based on LR NURBS and its application to contact. Comput Mech 60(1):1–20

    MathSciNet  Google Scholar 

  16. Ciarlet PG (1988) Mathematical elasticity, I: three-dimensional elasticity. Vol. 20 of Stud. Math. Appl. Elsevier, Amsterdam

  17. Mooney M (1940) A theory of large elastic deformation. J Appl Phys 11(9):582–592

    Article  Google Scholar 

  18. Rivlin R (1948) Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos Trans R Soc Lond A. 241(835):379–397

  19. Kim N-H (2014) Introduction to nonlinear finite element analysis. Springer, Berlin

    Google Scholar 

  20. Hassani B, Hinton E (2012) Homogenization and structural topology optimization: theory, practice and software. Springer, Berlin

    MATH  Google Scholar 

  21. Wriggers P (2003) Computational contact mechanics. Comput Mech 32(1):141

    Article  Google Scholar 

  22. Matzen ME, Cichosz T, Bischoff M (2013) A point to segment contact formulation for isogeometric, NURBS based finite elements. Comput Methods Appl Mech Eng 255:27–39

    Article  MathSciNet  Google Scholar 

  23. Piegl L, Tiller W (2012) The NURBS book. Springer, Berlin

    MATH  Google Scholar 

  24. Cottrell JA, Hughes TJ, Bazilevs Y (2009) Isogeometric analysis: toward integration of CAD and FEA. Wiley, Hoboken

    Book  Google Scholar 

  25. De Lorenzis L, Wriggers P, Hughes TJ (2014) Isogeometric contact: a review. GAMM-Mitteilungen 37(1):85–123

    Article  MathSciNet  Google Scholar 

  26. Lu J, Zheng C (2014) Dynamic cloth simulation by isogeometric analysis. Comput Methods Appl Mech Eng 268:475–493

    Article  MathSciNet  Google Scholar 

  27. Hughes TJ, Reali A, Sangalli G (2010) Efficient quadrature for NURBS-based isogeometric analysis. Comput Methods Appl Mech Eng 199(5–8):301–313

    Article  MathSciNet  Google Scholar 

  28. Cottrell J, Hughes T, Reali A (2007) Studies of refinement and continuity in isogeometric structural analysis. Comput Methods Appl Mech Eng 196(41–44):4160–4183

    Article  Google Scholar 

  29. Babuvška I, Rheinboldt WC (1978) Error estimates for adaptive finite element computations. SIAM J Numer Anal 15(4):736–754

    Article  MathSciNet  Google Scholar 

  30. Zienkiewicz OC, Zhu JZ (1987) A simple error estimator and adaptive procedure for practical engineerng analysis. Int J Numer Methods Eng 24(2):337–357

    Article  Google Scholar 

  31. Lee N-S, Bathe K-J (1994) Error indicators and adaptive remeshing in large deformation finite element analysis. Finite Elem Anal Des 16(2):99–139

    Article  MathSciNet  Google Scholar 

  32. Wriggers P, Scherf O (1998) Adaptive finite element techniques for frictional contact problems involving large elastic strains. Comput Methods Appl Mech Eng 151(3–4):593–603

    Article  MathSciNet  Google Scholar 

  33. Johnson C, Hansbo P (1992) Adaptive finite element methods in computational mechanics. Comput Methods Appl Mech Eng 101(1–3):143–181

    Article  MathSciNet  Google Scholar 

  34. Carstensen C, Scherf O, Wriggers P (1999) Adaptive finite elements for elastic bodies in contact. SIAM J Sci Comput 20(5):1605–1626

    Article  MathSciNet  Google Scholar 

  35. Szabó B, Szabo BA, Babuška I (1991) Finite element analysis. Wiley, Hoboken

    MATH  Google Scholar 

  36. Johnson KL, Johnson KL (1987) Contact mechanics. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  37. Shigley J, Mischke C, Budynas R (2004) Shigley's mechanical engineering design, 7th edn. McGraw-Hill, New York

    Google Scholar 

  38. Da Veiga LB, Buffa A, Rivas J, Sangalli G (2011) Some estimates for h–p–k-refinement in isogeometric analysis. Numer Math 118(2):271–305

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Ferdowsi University of Mashhad, Mashhad, Iran

    Emad Bidkhori & Behrooz Hassani

Authors
  1. Emad Bidkhori
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Behrooz Hassani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Behrooz Hassani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bidkhori, E., Hassani, B. A parametric knot adaptation approach to isogeometric analysis of contact problems. Engineering with Computers 38, 609–630 (2022). https://doi.org/10.1007/s00366-020-01073-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01073-0

Keywords