Skip to main content
Springer Nature Link
Log in

Shifted Chebyshev collocation of the fourth kind with convergence analysis for the space–time fractional advection-diffusion equation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

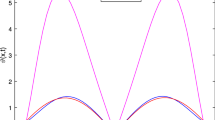
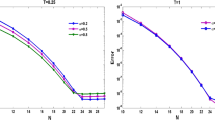
The main purpose of this paper is to design a numerical method for solving the space–time fractional advection-diffusion equation (STFADE). First, a finite difference scheme is applied to obtain the semi-discrete in time variable with convergence order \(\mathcal {O}(\tau ^{2-\beta })\). In the next, to discrete the spatial fractional derivative, the Chebyshev collocation method of the fourth kind has been applied. This discrete scheme is based on the closed formula for the spatial fractional derivative. Besides, the time-discrete scheme has studied in the \(L_{2}\) space by the energy method and we have proved the unconditional stability and convergence order. Finally, we solve three examples by the proposed method and the obtained results are compared with other numerical problems. The numerical results show that our method is much more accurate than existing techniques in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Aghdam YE, Mesgrani H, Javidi M, Nikan O (2020) A computational approach for the space-time fractional advection–diffusion equation arising in contaminant transport through porous media. Engineering with Computers pp. 1–16. https://doi.org/10.1007/s00366-020-01021-y

  2. Alavizadeh S, Ghaini FM (2015) Numerical solution of fractional diffusion equation over a long time domain. Applied Mathematics and Computation 263:240–250

    Article  MathSciNet  Google Scholar 

  3. Atangana A, Gómez-Aguilar J (2018) Numerical approximation of Riemann-Liouville definition of fractional derivative: from Riemann-Liouville to Atangana-Baleanu. Numerical Methods for Partial Differential Equations 34(5):1502–1523

    Article  MathSciNet  Google Scholar 

  4. Baseri A, Abbasbandy S, Babolian E (2018) A collocation method for fractional diffusion equation in a long time with chebyshev functions. Applied Mathematics and Computation 322:55–65

    Article  MathSciNet  Google Scholar 

  5. Ervin VJ, Roop JP (2006) Variational formulation for the stationary fractional advection dispersion equation. Numerical Methods for Partial Differential Equations: An International Journal 22(3):558–576

    Article  MathSciNet  Google Scholar 

  6. Ervin VJ, Roop JP (2007) Variational solution of fractional advection dispersion equations on bounded domains in \(\mathbb{R}^{d}\). Numerical Methods for Partial Differential Equations: An International Journal 23(2):256–281

    Article  MathSciNet  Google Scholar 

  7. Gómez-Aguilar J, Atangana A (2017) New insight in fractional differentiation: power, exponential decay and Mittag-Leffler laws and applications. The European Physical Journal Plus 132(1):13

    Article  Google Scholar 

  8. Goufo EFD, Kumar S, Mugisha S (2020) Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos, Solitons & Fractals 130:109467

    Article  MathSciNet  Google Scholar 

  9. Huang J, Nie N, Tang Y (2014) A second order finite difference-spectral method for space fractional diffusion equations. Science China Mathematics 57(6):1303–1317

    Article  MathSciNet  Google Scholar 

  10. Kemppainen J (2011) Existence and uniqueness of the solution for a time-fractional diffusion equation with robin boundary condition. In: Abstract and Applied Analysis, vol. 2011. Hindawi

  11. Khader M (2011) On the numerical solutions for the fractional diffusion equation. Communications in Nonlinear Science and Numerical Simulation 16(6):2535–2542

    Article  MathSciNet  Google Scholar 

  12. Khader M, Sweilam N, Mahdy A (2011) An efficient numerical method for solving the fractional diffusion equation. Journal of Applied Mathematics and Bioinformatics 1(2):1

    MATH  Google Scholar 

  13. Kumar A, Kumar S, Yan SP (2017) Residual power series method for fractional diffusion equations. Fundamenta Informaticae 151(1–4):213–230

    Article  MathSciNet  Google Scholar 

  14. Kumar K, Pandey RK, Sharma S (2017) Comparative study of three numerical schemes for fractional integro-differential equations. Journal of Computational and Applied Mathematics 315:287–302

    Article  MathSciNet  Google Scholar 

  15. Kumar S, Ghosh S, Samet B, Goufo EFD (2020) An analysis for heat equations arises in diffusion process using new Yang-Abdel-Aty-Cattani fractional operator. Mathematical Methods in the Applied Sciences 43(9):6062–6080

    Article  MathSciNet  Google Scholar 

  16. Kumar S, Kumar A, Argyros IK (2017) A new analysis for the keller-segel model of fractional order. Numerical Algorithms 75(1):213–228

    Article  MathSciNet  Google Scholar 

  17. Kumar S, Kumar R, Cattani C, Samet B (2020) Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons & Fractals 135:109811

    Article  MathSciNet  Google Scholar 

  18. Liu F, Anh VV, Turner I, Zhuang P (2003) Time fractional advection-dispersion equation. Journal of Applied Mathematics and Computing 13(1–2):233

    Article  MathSciNet  Google Scholar 

  19. Liu F, Zhuang P, Anh V, Turner I, Burrage K (2007) Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation. Applied Mathematics and Computation 191(1):12–20

    Article  MathSciNet  Google Scholar 

  20. Metzler R, Klafter J (2000) The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Physics reports 339(1):1–77

    Article  MathSciNet  Google Scholar 

  21. Nikan O, Golbabai A, Machado JT, Nikazad T (2020) Numerical approximation of the time fractional cable equation arising in neuronal dynamics. Engineering with Computers pp. 1–19. https://doi.org/10.1007/s00366-020-01033-8

  22. Nikan O, Machado JT, Golbabai A, Nikazad T (2020) Numerical approach for modeling fractal mobile/immobile transport model in porous and fractured media. International Communications in Heat and Mass Transfer 111:104443

    Article  Google Scholar 

  23. Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, vol 198. Elsevier, New York

    MATH  Google Scholar 

  24. Quarteroni A, Valli A (2008) Numerical approximation of partial differential equations, vol. 23. Springer Science & Business Media

  25. Safdari H, Mesgarani H, Javidi M, Aghdam YE (2020) Convergence analysis of the space fractional-order diffusion equation based on the compact finite difference scheme. Comput. Appl. Math 39(2):1–15

    Article  MathSciNet  Google Scholar 

  26. Tadjeran C, Meerschaert MM, Scheffler HP (2006) A second-order accurate numerical approximation for the fractional diffusion equation. Journal of Computational Physics 213(1):205–213

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

José Francisco Gómez Aguilar affirms the help provided by CONACyT, Mexico: Cátedras CONACyT para jóvenes investigators 2014 and SNI-CONACyT, Mexico.

Author information

Authors and Affiliations

  1. Faculty of Science, Shahid Rajaee Teacher Training University, Lavizan, Tehran, 16785-163, Iran

    H. Safdari & Y. Esmaeelzade Aghdam

  2. CONACyT-Tecnológico Nacional de México/CENIDET, Interior Internado Palmira S/N, Col. Palmira, C.P. 62490, Cuernavaca, Morelos, Mexico

    J. F. Gómez-Aguilar

Authors
  1. H. Safdari
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Y. Esmaeelzade Aghdam
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. J. F. Gómez-Aguilar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to J. F. Gómez-Aguilar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Safdari, H., Aghdam, Y.E. & Gómez-Aguilar, J.F. Shifted Chebyshev collocation of the fourth kind with convergence analysis for the space–time fractional advection-diffusion equation. Engineering with Computers 38, 1409–1420 (2022). https://doi.org/10.1007/s00366-020-01092-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01092-x

Keywords

Mathematics Subject Classification