Skip to main content
Springer Nature Link
Log in

The smooth transition GARCH model for simulation of highly nonstationary earthquake ground motions

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

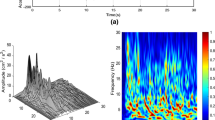
The aim of this paper is to extend a stochastic model for simulation of highly nonstationary ground motions (GMs). In this model, the dual-tree complex discrete wavelet transform (DT-CDWT) is applied to a recorded ground motion to extract its wavelet coefficients and then the Smooth Transition Generalized Autoregressive Conditional Heteroscedastic (ST-GARCH) model is used to simulate these coefficients. This model simulates nonstationary features of real GMs greatly, because the conditional variance estimated by this model changes compatibly with the amplitude nonstationary features of real GMs. Because of having asymmetric structure, this model also estimates sudden changes in the amplitude of ground motions. Some of the special capabilities of this model are the simulation of multiple increasing–decreasing cycles in the temporal amplitude of GMs, prediction of several peaks in the frequency spectrum of GMs, estimation of steps of their energy curve, and simultaneous simulation of all shocks of a GM sequence. Also, this model simulates the time–frequency energy distribution of both wide-frequency and narrow-frequency bandwidth GMs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Grigoriu M (2011) To scale or not to scale seismic ground-acceleration records. J Eng Mech 137:284–293

    Google Scholar 

  2. Somerville PG, Smith NF, Graves RW, Abrahamson NA (1997) Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seismol Res Lett 68:199–222

    Google Scholar 

  3. Hartzell S, Guatteri M, Mai PM et al (2005) Calculation of broadband time histories of ground motion, Part II: Kinematic and dynamic modeling using theoretical Green’s functions and comparison with the 1994 Northridge earthquake. Bull Seismol Soc Am 95:614–645

    Google Scholar 

  4. Rezaeian S, Der Kiureghian A (2008) A stochastic ground motion model with separable temporal and spectral nonstationarities. Earthq Eng Struct Dyn 37:1565–1584

    Google Scholar 

  5. Graves RW, Pitarka A (2010) Broadband ground-motion simulation using a hybrid approach. Bull Seismol Soc Am 100:2095–2123

    Google Scholar 

  6. Stafford PJ, Sgobba S, Marano GC (2009) An energy-based envelope function for the stochastic simulation of earthquake accelerograms. Soil Dyn Earthq Eng 29:1123–1133

    Google Scholar 

  7. Ruiz P, Penzien J (1971) Stochastic seismic response of structures. J Eng Mech (ASCE) 97:441–456

    Google Scholar 

  8. Mobarakeh AA, Rofooei FR, Ahmadi G (2002) Simulation of earthquake records using time-varying ARMA (2,1) model. Probab Eng Mech 17:15–34

    Google Scholar 

  9. Wang L, McCullough M, Kareem A (2014) Modeling and simulation of nonstationary processes utilizing wavelet and Hilbert transforms. J Eng Mech 140:345–360

    Google Scholar 

  10. Zhang Y, Zhao F, Yang C (2015) Generation of nonstationary ground motions compatible with multidamping response spectra. Bull Seismol Soc Am 105:341–353

    Google Scholar 

  11. Zhang Y, Zhao F (2010) Artificial ground motion compatible with specified peak ground displacement and target multi-damping response spectra. Nucl Eng Des 240:2571–2578

    Google Scholar 

  12. Sabetta F, Pugliese A (1996) Estimation of response spectra and simulation of nonstationary earthquake ground motions. Bull Seismol Soc Am 86:337–352

    Google Scholar 

  13. Yeh C-H, Wen YK (1990) Modeling of nonstationary ground motion and analysis of inelastic structural response. Struct Saf 8:281–298

    Google Scholar 

  14. Papadimitriou K (1990) Stochastic characterization of strong ground motion and application to structural response. Report No. EERL 90-03, Earthquake Engineering Research Laboratory, California Institute of Technology, Pasadena, CA

  15. Rezaeian S, Der Kiureghian A (2010) Simulation of synthetic ground motions for specified earthquake and site characteristics. Earthq Eng Struct Dyn 39:1155–1180

    Google Scholar 

  16. Rezaeian S, Der Kiureghian A (2012) Simulation of orthogonal horizontal ground motion components for specified earthquake and site characteristics. Earthq Eng Struct Dyn 41:335–353

    Google Scholar 

  17. Medel-Vera C, Ji T (2016) A stochastic ground motion accelerogram model for Northwest Europe. Soil Dyn Earthq Eng 82:170–195

    Google Scholar 

  18. Tsioulou A, Taflanidis AA, Galasso C (2018) Modification of stochastic ground motion models for matching target intensity measures. Earthq Eng Struct Dyn 47:3–24

    Google Scholar 

  19. Vetter CR, Taflanidis AA, Mavroeidis GP (2016) Tuning of stochastic ground motion models for compatibility with ground motion prediction equations. Earthq Eng Struct Dyn 45:893–912

    Google Scholar 

  20. Yamamoto Y, Baker JW (2013) Stochastic model for earthquake ground motion using wavelet packets. Bull Seismol Soc Am 103:3044–3056

    Google Scholar 

  21. Huang D, Wang G (2015) Stochastic simulation of regionalized ground motions using wavelet packets and cokriging analysis. Earthq Eng Struct Dyn 44:775–794

    Google Scholar 

  22. Hazirbaba YD, Tezcan J (2016) Image based modeling and prediction of nonstationary ground motions. Comput Struct 174:85–91

    Google Scholar 

  23. Tezcan J, Cheng J, Cheng Q (2014) Modeling and prediction of nonstationary ground motions as time–frequency images. IEEE Trans Geosci Remote Sens. https://doi.org/10.1109/TGRS.2014.2347335

    Article  Google Scholar 

  24. Wang D, Fan Z, Hao S, Zhao D (2018) An evolutionary power spectrum model of fully nonstationary seismic ground motion. Soil Dyn Earthq Eng 105:1–10

    Google Scholar 

  25. Sharbati R, Khoshnoudian F, Ramazi HR, Amindavar HR (2018) Stochastic modeling and simulation of ground motions using complex discrete wavelet transform and Gaussian mixture model. Soil Dyn Earthq Eng 114:267–280

    Google Scholar 

  26. Sharbati R, Khoshnoudian F, Koopialipoor M, Tahir MM (2019) Applying dual-tree complex discrete wavelet transform and gamma modulating function for simulation of ground motions. Eng Comput. https://doi.org/10.1007/s00366-019-00898-8

    Article  Google Scholar 

  27. Sharbati R, Ramazi HR, Khoshnoudian F et al (2019) Stochastic model for simulation of ground-motion sequences using kernel-based smoothed wavelet transform and Gaussian mixture distribution. J Earthq Eng. https://doi.org/10.1080/13632469.2019.1605948

    Article  Google Scholar 

  28. Vlachos C, Papakonstantinou KG, Deodatis G (2016) A multi-modal analytical non-stationary spectral model for characterization and stochastic simulation of earthquake ground motions. Soil Dyn Earthq Eng 80:177–191

    Google Scholar 

  29. Vlachos C, Papakonstantinou KG, Deodatis G (2018) Predictive model for site specific simulation of ground motions based on earthquake scenarios. Earthq Eng Struct Dyn 47:195–218

    Google Scholar 

  30. Oruç Ö (2019) An efficient wavelet collocation method for nonlinear two-space dimensional Fisher–Kolmogorov–Petrovsky–Piscounov equation and two-space dimensional extended Fisher-Kolmogorov equation. Eng Comput. https://doi.org/10.1007/s00366-019-00734-z

    Article  Google Scholar 

  31. Kumar KH, Vijesh VA (2019) Legendre wavelet-based iterative schemes for fourth-order elliptic equations with nonlocal boundary conditions. Eng Comput. https://doi.org/10.1007/s00366-019-00766-5

    Article  Google Scholar 

  32. Sharbati R, Rahimi R, Koopialipoor MR et al (2020) Detection and extraction of velocity pulses of near-fault ground motions using asymmetric Gaussian chirplet model. Soil Dyn Earthq Eng 133:106123

    Google Scholar 

  33. Mallat S (2009) A wavelet tour of signal processing: the sparce way. Elsevier, Amsterdam

    MATH  Google Scholar 

  34. Zhu XX, Bamler R (2010) Tomographic SAR inversion by $ L_ 1 $-norm regularization—The compressive sensing approach. IEEE Trans Geosci Remote Sens 48:3839–3846

    Google Scholar 

  35. Beckouche S, Ma J (2014) Simultaneous dictionary learning and denoising for seismic data. Geophysics 79:A27–A31

    Google Scholar 

  36. Boßmann F, Ma J (2016) Asymmetric chirplet transform—part 2: Phase, frequency, and chirp rate asymmetric chirplet transform: part 2. Geophysics 81:V425–V439

    Google Scholar 

  37. Tao C, Pan H, Li Y, Zou Z (2015) Unsupervised spectral–spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification. IEEE Geosci Remote Sens Lett 12:2438–2442

    Google Scholar 

  38. Kuyuk HS, Yildirim E, Dogan E, Horasan G (2012) Application of k-means and Gaussian mixture model for classification of seismic activities in Istanbul. Nonlinear Process Geophys 19:411–419

    Google Scholar 

  39. Baker JW (2007) Quantitative classification of near-fault ground motions using wavelet analysis. Bull Seismol Soc Am 97:1486–1501

    Google Scholar 

  40. Kingsbury N (1999) Image processing with complex wavelets. Philos Trans R Soc London Ser A Math Phys Eng Sci 357:2543–2560

    MATH  Google Scholar 

  41. Bollerslev T (1996) Fractionally integrated generalized autoregressive conditional heteroskedasticity. J Econ 74:3–30

    MathSciNet  MATH  Google Scholar 

  42. Engle RF (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econ J Econ Soc 50:987–1007

    MathSciNet  MATH  Google Scholar 

  43. González-Rivera G (1998) Smooth-transition GARCH models. Stud Nonlinear Dyn Econ 3:61–78

    MATH  Google Scholar 

  44. Lubrano M (2001) Smooth transition GARCH models: a Bayesian perspective. Rech Econ Louvain 67:257–287

    Google Scholar 

  45. Haas M, Krause J, Paolella MS, Steude SC (2013) Time-varying mixture GARCH models and asymmetric volatility. N Am J Econ Financ 26:602–623

    Google Scholar 

  46. Medeiros MC, Veiga A (2009) Modeling multiple regimes in financial volatility with a flexible coefficient GARCH (1, 1) model. Econ Theory 25:117–161

    MathSciNet  MATH  Google Scholar 

  47. Boashash B, Khan NA, Ben-Jabeur T (2015) Time–frequency features for pattern recognition using high-resolution TFDs: A tutorial review. Dig Signal Process 40:1–30

    MathSciNet  Google Scholar 

  48. PEER P (2014) Ground motion database. https://peer.berkeley.edu/peer_ground_motion_database. Accessed 26 Mar 2014.

  49. Conte JP, Peng BF (1997) Fully nonstationary analytical earthquake ground-motion model. J Eng Mech 123:15–24

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Civil and Environmental Engineering, Amirkabir University of Technology, Tehran, 15914, Iran

    Reza Sharbati, Faramarz Khoshnoudian & Mohammadreza Koopialipoor

  2. Faculty of Mining and Metallurgical Engineering, Amirkabir University of Technology, Tehran, 15914, Iran

    Hamidreza Ramazi

  3. Faculty of Statistics, Amirkabir University of Technology, Tehran, 15914, Iran

    Toktam Valizadeh

  4. Institute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam

    Danial Jahed Armaghani

Authors
  1. Reza Sharbati
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hamidreza Ramazi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Faramarz Khoshnoudian
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Toktam Valizadeh
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Mohammadreza Koopialipoor
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Danial Jahed Armaghani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Danial Jahed Armaghani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharbati, R., Ramazi, H., Khoshnoudian, F. et al. The smooth transition GARCH model for simulation of highly nonstationary earthquake ground motions. Engineering with Computers 38, 1529–1541 (2022). https://doi.org/10.1007/s00366-020-01117-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01117-5

Keywords