Skip to main content
SpringerLink
Log in

A new variable-order fractional derivative with non-singular Mittag–Leffler kernel: application to variable-order fractional version of the 2D Richard equation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

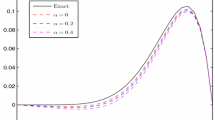
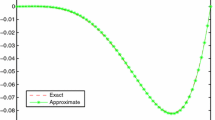
In this study, to overcome the limitations of non-singular fractional derivatives in the Caputo–Fabrizio and Atangana–Baleanu senses (especially in dealing with the variable-order (VO) fractional calculus), we introduce a new non-singular VO fractional derivative with Mittag–Leffler function as its kernel. Some useful results are derived from this fractional derivative. Moreover, this fractional derivative is used for introducing the VO fractional version of the 2D Richard equation. A meshless scheme based on the thin plate spline radial basis functions (RBFs) is developed for solving this equation. The validity of the formulated method is investigated through three numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Podlubny I (1999) Fractional Differential equations. Academic Press, San Diego

    MATH  Google Scholar 

  2. Caputo M, Fabrizio M (2015) A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl 1(2):1–13

    Google Scholar 

  3. Atangana A, Baleanu D (2016) New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Thermal Sci 20(2):763–769

    Article  Google Scholar 

  4. Samko SG (2013) Fractional integration and differentiation of variable order: an overview. Nonlinear Dyn 71:653–662

    Article  MathSciNet  Google Scholar 

  5. Sun HG, Chen W, Wei H, Chen YQ (2011) A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur Phys J Spec Top 193:185–192

    Article  Google Scholar 

  6. Heydari MH, Avazzadeh Z (2018) An operational matrix method for solving variable-order fractional biharmonic equation. Comput Appl Math 37(4):4397–4411

    Article  MathSciNet  Google Scholar 

  7. Heydari MH (2018) A new direct method based on the Chebyshev cardinal functions for variable-order fractional optimal control problems. J Franklin Inst 355:4970–4995

    Article  MathSciNet  Google Scholar 

  8. Hosseininia M, Heydari MH, Maalek Ghaini FM, Avazzadeh Z (2019) A wavelet method to solve nonlinear variable-order time fractional 2D Klein-Gordon equation. Comput Math Appl 78:3713–3730

    Article  MathSciNet  Google Scholar 

  9. Hosseininia M, Heydari MH, Maalek Ghaini FM, Avazzadeh Z (2018) Two-dimensional Legendre wavelets for solving variable-order fractional nonlinear advection-diffusion equation with variable coefficients. Int J Nonlinear Sci Numer Simul 19:793–802

    Article  MathSciNet  Google Scholar 

  10. Heydari MH, Avazzadeh Z (2020) Numerical study of non-singular variable-order time fractional coupled burgers’ equations by using the Hahn polynomials. Eng Comput. https://doi.org/10.1007/s00366-020-01036-5

    Article  Google Scholar 

  11. Heydari MH, Avazzadeh Z (2020) Orthonormal Bernstein polynomials for solving nonlinear variable-order time fractional fourth-order diffusion-wave equation with nonsingular fractional derivative. Math Methods Appl Sci. https://doi.org/10.1002/mma.6483

    Article  MATH  Google Scholar 

  12. Bouhamidi A, Jbilou K (2008) Meshless thin plate spline methods for the modified Helmholtz equation. Comput Methods Appl Mech Eng 197:3733–3741

    Article  MathSciNet  Google Scholar 

  13. Mohebbi A, Saffarian M (2020) Implicit RBF meshless method for the solution of two dimensional variable order fractional cable equation. J Appl Comput Mech 6(2):235–247

    Google Scholar 

  14. Assari P, Adibi H, Dehghan M (2013) A meshless method for solving nonlinear two-dimensional integral equations of the second kind on non-rectangular domains using radial basis functions with error analysis. J Comput Appl Math 239:72–92

    Article  MathSciNet  Google Scholar 

  15. Assari P, Dehghan M (2018) A meshless Galerkin scheme for the approximate solution of nonlinear logarithmic boundary integral equations utilizing radial basis functions. J Comput Appl Math 333:362–381

    Article  MathSciNet  Google Scholar 

  16. Pachepsky Y, Timlin D, Rawls W (2003) Generalized Richards equation to simulate water transport in unsaturated soils. J Hydrol 272:3–13

    Article  Google Scholar 

  17. Montazeri Namin M, Boroomand MR (2012) A time splitting algorithm for numerical solution of Richard’s equation. J Hydrol 444:10–21

    Article  Google Scholar 

  18. Gerolymatou E, Vardoulakis I, Hilfer R (2006) Modelling infiltration by means of a nonlinear fractional diffusion model. J Phys D Appl Phys 39:4104–4110

    Article  Google Scholar 

  19. Qin X, Yang X (2019) A finite point method for solving the time fractional Richards equation. Math Probl Eng

  20. Freitas AA, Vigo DGA, Teixeira MG, Vasconcellos CABd (2017) Horizontal water flow in unsaturated porous media using a fractional integral method with an adaptive time step. Appl Math Modell 48:584–592

    Article  MathSciNet  Google Scholar 

  21. Hu DL, Chen W, Liang YJ (2019) Inverse Mittag-Leffler stability of structural derivative nonlinear dynamical systems. Chaos, Solitons Fractals 123:304–308

    Article  MathSciNet  Google Scholar 

  22. Liang YJ, Sandev T, Lenzi EK (2020) Reaction and ultraslow diffusion on comb structures. Phys Rev E 101(4):042119

    Article  MathSciNet  Google Scholar 

  23. Losada J, Nieto JJ (2015) Properties of a new fractional derivative without singular kernel. Prog Fract Differ Appl 1(2):87–92

    Google Scholar 

  24. Loh JR, Isah A, Phang C, Toh YT (2018) On the new properties of Caputo-Fabrizio operator and its application in deriving shifted Legendre operational matrix. Appl Numer Math 132:138–153

    Article  MathSciNet  Google Scholar 

  25. Baxter BJC (1992) The interpolation theory of radial basis functions. Cambridge University, Cambridge

    Google Scholar 

  26. Buhmann MD (2003) Radial basis functions. Cambridge university, Cambridge

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Shiraz University of Technology, Shiraz, Iran

    M. H. Heydari & M. Hosseininia

Authors
  1. M. H. Heydari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Hosseininia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. H. Heydari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Heydari, M.H., Hosseininia, M. A new variable-order fractional derivative with non-singular Mittag–Leffler kernel: application to variable-order fractional version of the 2D Richard equation . Engineering with Computers 38, 1759–1770 (2022). https://doi.org/10.1007/s00366-020-01121-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01121-9

Keywords

Search

Navigation