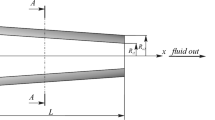
Abstract
As a first attempt, the vibration and stability analysis of magnetically embedded spinning axially functionally graded (AFG) nanotubes conveying fluid under axial loads is performed based on the nonlocal strain gradient theory (NSGT). A detailed parametric investigation is conducted to elucidate the influence of key factors such as material distribution type and size-dependent parameters on the divergence and flutter instability borders. Also, a comparative study is conducted to evaluate the available theories in the modeling of nanofluidic systems. The material characteristics of the system are graded along the longitudinal direction based on the power-law and exponential distribution functions. To accurate model and formulate the system, the no-slip boundary condition is considered. Adopting the Laplace transform and Galerkin discretization technique, the governing size-dependent dynamical equations of the system are solved. The backward and forward natural frequencies, as well as critical fluid and spin velocities of the system, are extracted. Besides, an analytical approach is applied to identify the instability thresholds of the system. Dynamical configurations, Campbell diagrams, and stability maps are analyzed. Meanwhile, it is concluded that, in contrast to the influence of nonlocal and density gradient parameters, the increment of strain gradient and elastic modulus gradient parameters expands the stability regions and alleviate the destabilizing effect of the axial compressive load.
























Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Askarian A, Permoon M, Shakouri M (2020) Vibration analysis of pipes conveying fluid resting on a fractional Kelvin-Voigt viscoelastic foundation with general boundary conditions. Int J Mech Sci 226:105702
Ghayesh MH, Païdoussis MP (2010) Three-dimensional dynamics of a cantilevered pipe conveying fluid, additionally supported by an intermediate spring array. Int J Nonlinear Mech 45:507–524
Ghayesh MH, Païdoussis MP, Amabili M (2013) Nonlinear dynamics of cantilevered extensible pipes conveying fluid. J Sound Vib 332:6405–6418
Ghayesh MH, Amabili M, Païdoussis MP (2012) Thermo-mechanical phase-shift determination in Coriolis mass-flowmeters with added masses. J Fluids Struct 34:1–13
Mamaghani AE, Khadem S, Bab S (2016) Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dyn 86:1761–1795
Ebrahimi-Mamaghani A, Sotudeh-Gharebagh R, Zarghami R, Mostoufi N (2019) Dynamics of two-phase flow in vertical pipes. J Fluids Struct 87:150–173
Liang F, Yang X-D, Zhang W, Qian Y-J (2019) Coupled bi-flexural–torsional vibration of fluid-conveying pipes spinning about an eccentric axis. Int J Struct Stab Dyn 19:1950003
Bahaadini R, Saidi AR (2018) Stability analysis of thin-walled spinning reinforced pipes conveying fluid in thermal environment. Eur J Mech A Solids 72:298–309
Liang F, Yang X-D, Qian Y-J, Zhang W (2018) Transverse free vibration and stability analysis of spinning pipes conveying fluid. Int J Mech Sci 137:195–204
Malikan M, Nguyen VB, Tornabene F (2018) Damped forced vibration analysis of single-walled carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Eng Sci Technol Int J 21:778–786
Malikan M, Dimitri R, Tornabene F (2019) Transient response of oscillated carbon nanotubes with an internal and external damping. Compos B Eng 158:198–205
Malikan M (2020) On the plastic buckling of curved carbon nanotubes. Theor Appl Mech Lett 10:46–56
Malikan M, Eremeyev VA (2020) Post-critical buckling of truncated conical carbon nanotubes considering surface effects embedding in a nonlinear Winkler substrate using the Rayleigh-Ritz method. Mater Res Express 7:025005
Torkaman-Asadi M, Rahmanian M, Firouz-Abadi R (2015) Free vibrations and stability of high-speed rotating carbon nanotubes partially resting on Winkler foundations. Compos Struct 126:52–61
Ilkhani M, Nazemnezhad R (2019) Molecular dynamics simulation and size dependent cylindrical shell models for vibrations of spinning axially loaded carbon nanotubes. Eur J Mech A Solids 77:103804
Hosseini-Hashemi S, Ilkhani M (2016) Exact solution for free vibrations of spinning nanotube based on nonlocal first order shear deformation shell theory. Compos Struct 157:1–11
SafarPour H, Ghadiri M (2017) Critical rotational speed, critical velocity of fluid flow and free vibration analysis of a spinning SWCNT conveying viscous fluid. Microfluid Nanofluid 21:22
Ghayesh MH (2019) Viscoelastic dynamics of axially FG microbeams. Int J Eng Sci 135:75–85
Ghayesh MH (2019) Viscoelastic mechanics of Timoshenko functionally graded imperfect microbeams. Compos Struct 225:110974
Ghayesh MH (2019) Mechanics of viscoelastic functionally graded microcantilevers. Eur J Mech A Solids 73:492–499
Ghayesh MH (2018) Dynamics of functionally graded viscoelastic microbeams. Int J Eng Sci 124:115–131
Ghayesh MH (2019) Asymmetric viscoelastic nonlinear vibrations of imperfect AFG beams. Appl Acoust 154:121–128
Ghayesh MH (2019) Dynamical analysis of multilayered cantilevers. Commun Nonlinear Sci Numer Simul 71:244–253
Mirtalebi H, Ebrahimi Mamaghani A (2018) On the dynamics of micro-tubes conveying fluid on various foundations. Amirkabir J Mech Eng 52:1–10
Babaei A, Rahmani A (2020) Vibration analysis of rotating thermally-stressed gyroscope, based on modified coupled displacement field method. Mech Based Des Struct Mach. https://doi.org/10.1080/15397734.2020.1713156
Ghazavi M, Molki H (2018) Nonlinear analysis of the micro/nanotube conveying fluid based on second strain gradient theory. Appl Math Model 60:77–93
Ebrahimi-Mamaghani A, Mirtalebi SH, Ahmadian M-T (1250c) Magneto-mechanical stability of axially functionally graded supported nanotubes. Mater Res Express 6:1250c5
Esfahani S, Esmaeilzade Khadem S, Ebrahimi Mamaghani A (2019) Size-dependent nonlinear vibration of an electrostatic nanobeam actuator considering surface effects and inter-molecular interactions. Int J Mech Mater Design 15:489–505
Esfahani S, Khadem SE, Mamaghani AE (2019) Nonlinear vibration analysis of an electrostatic functionally graded nano-resonator with surface effects based on nonlocal strain gradient theory. Int J Mech Sci 151:508–522
Lim C, Zhang G, Reddy J (2015) A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids 78:298–313
Malikan M, Nguyen VB (2018) Buckling analysis of piezo-magnetoelectric nanoplates in hygrothermal environment based on a novel one variable plate theory combining with higher-order nonlocal strain gradient theory. Phys E Lowdimensional Syst Nanustructures 102:8–28
Malikan M, Nguyen VB, Dimitri R, Tornabene F (2019) Dynamic modeling of non-cylindrical curved viscoelastic single-walled carbon nanotubes based on the second gradient theory. Mater Res Express 6:075041
Malikan M, Eremeyev VA (2020) On the dynamics of a visco–piezo–flexoelectric nanobeam. Symmetry 12:643
Malikan M, Krasheninnikov M, Eremeyev VA (2020) Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int J Eng Sci 148:103210
Farajpour A, Ghayesh MH, Farokhi H (2019) Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes. Int J Mech Sci 150:510–525
Shen J, Wang P, Li C, Wang Y (2019) New observations on transverse dynamics of microtubules based on nonlocal strain gradient theory. Compos Struct 225:111036
Ghane M, Saidi AR, Bahaadini R (2020) Vibration of fluid-conveying nanotubes subjected to magnetic field based on the thin-walled Timoshenko beam theory. Appl Math Model 80:65–83
Mahinzare M, Mohammadi K, Ghadiri M (2019) A nonlocal strain gradient theory for vibration and flutter instability analysis in rotary SWCNT with conveying viscous fluid. Waves Random Complex Media. https://doi.org/10.1080/17455030.2019.1584420
Sarparast H, Ebrahimi-Mamaghani A (2019) Vibrations of laminated deep curved beams under moving loads. Compos Struct 226:111262
Ebrahimi-Mamaghani A, Sarparast H, Rezaei M (2020) On the vibrations of axially graded Rayleigh beams under a moving load. Appl Math Model 84:554–570
Safarpour M, Rahimi A, Alibeigloo A, Bisheh H, Forooghi A (2019) Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions. Mech Based Design Struct. https://doi.org/10.1080/15397734.2019.1701491
Alibeigloo A (2016) Thermo elasticity solution of sandwich circular plate with functionally graded core using generalized differential quadrature method. Compos Struct 136:229–240
Alibeigloo A (2014) Three-dimensional thermo-elasticity solution of sandwich cylindrical panel with functionally graded core. Compos Struct 107:458–468
Ghayesh MH (2018) Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl Math Model 59:583–596
Ghayesh MH (2019) Nonlinear oscillations of FG cantilevers. Appl Acoust 145:393–398
Ghayesh MH (2019) Resonant vibrations of FG viscoelastic imperfect Timoshenko beams. J Vib Control 25:1823–1832
Valiollahi A, Shojaeifard M, Baghani M (2019) Implementing stretch-based strain energy functions in large coupled axial and torsional deformations of functionally graded cylinder. Int J Appl Mech 11:1950039
Mirtalebi SH, Ebrahimi-Mamaghani A, Ahmadian MT (2019) Vibration control and manufacturing of intelligibly designed axially functionally graded cantilevered macro/micro-tubes. IFAC Pap Online 52:382–387
Eftekhari M, Hosseini M (2016) On the stability of spinning functionally graded cantilevered pipes subjected to fluid-thermomechanical loading. Int J Struct Stab Dyn 16:1550062
Setoodeh A, Afrahim S (2014) Nonlinear dynamic analysis of FG micro-pipes conveying fluid based on strain gradient theory. Compos Struct 116:128–135
Filiz S, Aydogdu M (2015) Wave propagation analysis of embedded (coupled) functionally graded nanotubes conveying fluid. Compos Struct 132:1260–1273
Deng J, Liu Y, Zhang Z, Liu W (2017) Size-dependent vibration and stability of multi-span viscoelastic functionally graded material nanopipes conveying fluid using a hybrid method. Compos Struct 179:590–600
Ebrahimi-Mamaghani A, Sotudeh-Gharebagh R, Zarghami R, Mostoufi N (2020) Thermo-mechanical stability of axially graded Rayleigh pipes. Mech Based Design Struct. https://doi.org/10.1080/15397734.2020.1717967
Li X, Li L, Hu Y, Ding Z, Deng W (2017) Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos Struct 165:250–265
Mirramezani M, Mirdamadi HR (2012) Effects of nonlocal elasticity and Knudsen number on fluid–structure interaction in carbon nanotube conveying fluid. Phys E 44:2005–2015
Rashidi V, Mirdamadi HR, Shirani E (2012) A novel model for vibrations of nanotubes conveying nanoflow. Comput Mater Sci 51:347–352
Ghayesh MH, Amabili M (2013) Post-buckling bifurcations and stability of high-speed axially moving beams. Int J Mech Sci 68:76–91
Atashafrooz M, Bahaadini R, Sheibani HR (2020) Nonlocal, strain gradient and surface effects on vibration and instability of nanotubes conveying nanoflow. Mech Adv Mater Struct 27:586–598
Bahaadini R, Saidi AR, Hosseini M (2018) On dynamics of nanotubes conveying nanoflow. Int J Eng Sci 123:181–196
Sadeghi-Goughari M, Jeon S, Kwon H-J (2018) Flutter instability of cantilevered carbon nanotubes caused by magnetic fluid flow subjected to a longitudinal magnetic field. Phys E 98:184–190
Bahaadini R, Hosseini M (2016) Nonlocal divergence and flutter instability analysis of embedded fluid-conveying carbon nanotube under magnetic field. Microfluid Nanofluid 20:108
Valiollahi A, Shojaeifard M, Baghani M (2019) Closed form solutions for large deformation of cylinders under combined extension-torsion. Int J Mech Sci 157:336–347
Paidoussis MP (1998) Fluid-structure interactions: slender structures and axial flow, vol 1. Academic press, London
Wang L (2010) Size-dependent vibration characteristics of fluid-conveying microtubes. J Fluids Struct 26:675–684
Mamaghani AE, Zohoor H, Firoozbakhsh K, Hosseini R (2013) Dynamics of a running below-knee prosthesis compared to those of a normal subject. J Solid Mech 5:152–160
Sahlabadi M, Valiollahi A, Konh B, Soltani N (2017) Evaluating J-integral and Q parameter in high-density polyethylene using a combined experimental finite element method. Fatigue Fract Eng Mater Struct 40:924–938
Yang X-D, Yang J-H, Qian Y-J, Zhang W, Melnik RV (2018) Dynamics of a beam with both axial moving and spinning motion: an example of bi-gyroscopic continua. Eur J Mech A Solids 69:231–237
Mamaghani AE, Khadem SE, Bab S, Pourkiaee SM (2018) Irreversible passive energy transfer of an immersed beam subjected to a sinusoidal flow via local nonlinear attachment. Int J Mech Sci 138:427–447
Hosseini R, Hamedi M, Ebrahimi Mamaghani A, Kim HC, Kim J, Dayou J (2017) Parameter identification of partially covered piezoelectric cantilever power scavenger based on the coupled distributed parameter solution. Int J Smart Nano Mater 8:110–124
Moayedi H, Ebrahimi F, Habibi M, Safarpour H, Foong LK (2020) Application of nonlocal strain–stress gradient theory and GDQEM for thermo-vibration responses of a laminated composite nanoshell. Eng Comput. https://doi.org/10.1007/s00366-020-01002-1
Lori ES, Ebrahimi F, Supeni EEB, Habibi M, Safarpour H (2020) The critical voltage of a GPL-reinforced composite microdisk covered with piezoelectric layer. Eng Comput. https://doi.org/10.1007/s00366-020-01004-z
Abdelmalek Z, Karbon M, Eyvazian A, Forooghi A, Safarpour H, Tlili I (2020) On the dynamics of a curved microtubule-associated proteins by considering viscoelastic properties of the living biological cells. J Biomol Struct Dyn. https://doi.org/10.1080/07391102.2020.1747549
Jermsittiparsert K, Ghabussi A, Forooghi A, Shavalipour A, Habibi M, won Jung D, Safa M (2020) Critical voltage, thermal buckling and frequency characteristics of a thermally affected GPL reinforced composite microdisk covered with piezoelectric actuator. Mech Based Des Struct Mach. https://doi.org/10.1080/15397734.2020.1748052
Hu Y-G, Liew KM, Wang Q (2011) Nonlocal continuum model and molecular dynamics for free vibration of single-walled carbon nanotubes. J Nanosci Nanotechnol 11:10401–10407
Duan W, Wang CM, Zhang Y (2007) Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J Appl Phys 101:024305
Arash B, Ansari R (2010) Evaluation of nonlocal parameter in the vibrations of single-walled carbon nanotubes with initial strain. Phys E 42:2058–2064
Lu P, Lee H, Lu C, Zhang P (2006) Dynamic properties of flexural beams using a nonlocal elasticity model. J Appl Phys 99:073510
Lancaster P (2013) Stability of linear gyroscopic systems: a review. Linear Algebra Appl 439:686–706
Al-Furjan M, Safarpour H, Habibi M, Safarpour M, Tounsi A (2020) A comprehensive computational approach for nonlinear thermal instability of the electrically FG-GPLRC disk based on GDQ method. Eng Comput. https://doi.org/10.1007/s00366-020-01088-7
Safarpour M, Ebrahimi F, Habibi M, Safarpour H (2020) On the nonlinear dynamics of a multi-scale hybrid nanocomposite disk. Eng Comput. https://doi.org/10.1007/s00366-020-00949-5
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
The normalized eigenfunctions of nonlocal beams for P–P and C–C boundary conditions are as follow, respectively [77]:
where,
The characteristic frequency equation of abovementioned conditions are given as follows, respectively [77]:
Appendix 2
When the system is in the divergence instability condition, the minimum natural frequency of the system (the backward frequency) becomes zero. In this condition, the system loses its stiffness for the first mode. Consequently, to acquire the critical fluid (spin) velocity related to the first mode, by considering one mode (r = s = 1), Eq. (45) is reduced to the following equation:
By considering the linear variation for the material characteristics and ignoring the scale effects in the system, it can be written:
Based on the stability theory of the linear gyroscopic systems [78–80], when the eigenvalues of the system become zero, the determinant of the stiffness matrix equals zero. Therefore, the critical divergence fluid (spin) velocity of the system can be acquired from the following relation:
Rights and permissions
About this article
Cite this article
Zhu, X., Lu, Z., Wang, Z. et al. Vibration of spinning functionally graded nanotubes conveying fluid. Engineering with Computers 38, 1771–1792 (2022). https://doi.org/10.1007/s00366-020-01123-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-020-01123-7
Keywords
Profiles
- Ali Ebrahimi-Mamaghani View author profile