Skip to main content
Springer Nature Link
Log in

Two efficient numerical schemes for simulating dynamical systems and capturing chaotic behaviors with Mittag–Leffler memory

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

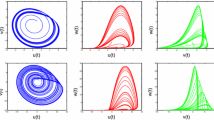
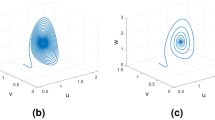
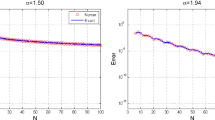
Abstract

In this paper, we consider two accurate iterative methods for solving fractional differential equations with power law and Mittag–Leffler kernel. We focused our attention on the stage-structured prey–predator model and several chaotic attractors of type Newton–Leipnik, Rabinovich–Fabrikant, Dadras, Aizawa, Thomas’ and 4 wings. The first algorithm is based on the trapezoidal product-integration rule, and the second one is based on Lagrange interpolations. The results obtained show that both numerical methods are very efficient and provide precise and outstanding results to determine approximate numerical solutions of fractional differential equations with non-local singular kernels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

References

  1. Caponetto R, Dongola G, Fortuna L, Petrás I (2010) Fractional order systems modeling and control applications. World Sci Ser Nonlinear Sci Ser A 77:177

    Google Scholar 

  2. Goufo EFD, Kumar S, Mugisha SB (2020) Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos, Solitons Fractals 130:1–10

    MathSciNet  MATH  Google Scholar 

  3. Ghanbari B, Kumar S, Kumar R (2020) A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos, Solitons Fractals 133:1–11

    MathSciNet  MATH  Google Scholar 

  4. Kumar S, Nisar KS, Kumar R, Cattani C, Samet B (2020) A new Rabotnov fractional-exponential function-based fractional derivative for diffusion equation under external force. Math Methods Appl Sci 43(7):4460–4471

    MathSciNet  MATH  Google Scholar 

  5. Kumar S, Kumar A, Abbas S, Al Qurashi M, Baleanu D (2020) A modified analytical approach with existence and uniqueness for fractional Cauchy reaction-diffusion equations. Adv Differ Equ 2020(1):1–18

    MathSciNet  MATH  Google Scholar 

  6. Kumar S, Kumar R, Agarwal RP, Samet B (2020) A study of fractional Lotka-Volterra population model using Haar wavelet and Adams-Bashforth-Moulton methods. Math Methods Appl Sci 43(8):5564–5578

    MathSciNet  MATH  Google Scholar 

  7. Alshabanat A, Jleli M, Kumar S, Samet B (2020) Generalization of Caputo-Fabrizio fractional derivative and applications to electrical circuits. Front Phys 8:1–13

    Google Scholar 

  8. Samko SG, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives: theory and applications. Gordon and Breach, Yverdon

    MATH  Google Scholar 

  9. Caputo M, Fabrizio M (2015) A new definition of fractional derivative without singular Kernel. Progr Fract Differ Appl 1:73–85

    Google Scholar 

  10. Atangana A, Baleanu D (2016) New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci 20:1–16

    Google Scholar 

  11. Mohyud-Din ST, Nawaz T, Azhar E, Akbar MA (2017) Fractional sub-equation method to space-time fractional Calogero-Degasperis and potential Kadomtsev-Petviashvili equations. J Taibah Univ Sci 11(2):258–263

    Google Scholar 

  12. Jafari H, Ghorbani M, Ghasempour S (2013) A note on exact solutions for nonlinear integral equations by a modified homotopy perturbation method. New Trends Math Sci 1(2):22–26

    Google Scholar 

  13. Sugiura H, Hasegawa T (2009) Quadrature rule for Abel’s equations: uniformly approximating fractional derivatives uniformly approximating fractional derivatives. J Comput Appl Math 223:459–468

    MathSciNet  MATH  Google Scholar 

  14. Rosenfeld JA, Dixon WE (2017) Approximating the Caputo fractional derivative through the Mittag-Leffler reproducing kernel Hilbert space and the kernelized Adams-Bashforth-Moulton method. SIAM J Numer Anal 55(3):1201–1217

    MathSciNet  MATH  Google Scholar 

  15. Diethelm K, Ford NJ, Freed AD (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29(1–4):3–22

    MathSciNet  MATH  Google Scholar 

  16. Diethelm K, Ford NJ, Freed AD (2004) Detailed error analysis for a fractional Adams method. Numer Algorithms 36(1):31–52

    MathSciNet  MATH  Google Scholar 

  17. Daftardar-Gejji V, Sukale Y, Bhalekar S (2014) A new predictor-corrector method for fractional differential equations. Appl Math Comput 244:158–182

    MathSciNet  MATH  Google Scholar 

  18. Asl MS, Javidi M (2017) An improved PC scheme for nonlinear fractional differential equations: error and stability analysis. J Comput Appl Math 324:101–117

    MathSciNet  MATH  Google Scholar 

  19. Gnitchogna R, Atangana A (2017) New two step laplace Adam-Bashforth method for integer a noninteger order partial differential equations. Numer Methods Partial Differ Equ 34(5):1739–1758

    MathSciNet  MATH  Google Scholar 

  20. Toufik M, Atangana A (2017) New numerical approximation of fractional derivative with non-local and non-singular kernel: application to chaotic models. Eur Phys J Plus 132(10):1–16

    Google Scholar 

  21. Li C, Yi Q, Chen A (2016) Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J Comput Phys 316:614–631

    MathSciNet  MATH  Google Scholar 

  22. Zhao L, Deng W (2014) Jacobian-predictor-corrector approach for fractional differential equations. Adv Comput Math 40(1):137–165

    MathSciNet  MATH  Google Scholar 

  23. Mishra J (2018) Fractional hyper-chaotic model with no equilibrium. Chaos Solitons Fractals 116:43–53

    MathSciNet  MATH  Google Scholar 

  24. Boubellouta A, Boulkroune A (2019) Intelligent fractional-order control-based projective synchronization for chaotic optical systems. Soft Comput 23(14):5367–5384

    MATH  Google Scholar 

  25. Deshpande A, Daftardar-Gejji V (2019) Chaotic dynamics of fractional Vallis system for El-Nino. Fract Calc Appl Anal 22(3):825–842

    MathSciNet  MATH  Google Scholar 

  26. Abdeljawad T, Baleanu D (2017) Integration by parts and its applications of a new nonlocal fractional derivative with Mittag-Leffler nonsingular kernel. J Nonlinear Sci Appl 10:1098–1107

    MathSciNet  MATH  Google Scholar 

  27. Arora C, Kumar V, Kant S (2017) Dynamics of a high-dimensional stage-structured prey-predator model. Int J Appl Comput Math 3(1):427–445

    MathSciNet  Google Scholar 

  28. Ghanbari B, Kumar D (2019) Numerical solution of predator-prey model with Beddington-DeAngelis functional response and fractional derivatives with Mittag-Leffler kernel. Chaos 29(6):1–12

    MathSciNet  MATH  Google Scholar 

  29. Diethelm K (1997) An algorithm for the numerical solution of differential equations of fractional order. Electron Trans Numer Anal 5(1):1–6

    MathSciNet  MATH  Google Scholar 

  30. Diethelm K, Ford NJ, Freed AD (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29(1–4):3–22

    MathSciNet  MATH  Google Scholar 

  31. Diethelm K, Ford NJ (2002) Analysis of fractional differential equations. J Math Anal Appl 265(2):229–248

    MathSciNet  MATH  Google Scholar 

  32. Diethelm K, Ford NJ, Freed AD (2004) Detailed error analysis for a fractional Adams method. Numer algorithms 36(1):31–52

    MathSciNet  MATH  Google Scholar 

  33. Diethelm K, Ford NJ, Freed AD, Luchko Y (2005) Algorithms for the fractional calculus: a selection of numerical methods. Comput Methods Appl Mech Eng 194(6–8):743–773

    MathSciNet  MATH  Google Scholar 

  34. Diethelm K, Ford NJ (2004) Multi-order fractional differential equations and their numerical solution. Appl Math Comput 154(3):621–640

    MathSciNet  MATH  Google Scholar 

  35. Hairer E, Lubich C, Schlichte M (1985) Fast numerical solution of nonlinear Volterra convolution equations. SIAM J Sci Stat Comput 6(3):532–541

    MathSciNet  MATH  Google Scholar 

  36. Diethelm K, Ford NJ, Freed AD (2004) Detailed error analysis for a fractional Adams method. Numer Algorithms 36(1):31–52

    MathSciNet  MATH  Google Scholar 

  37. Popolizio M (2018) Numerical solution of multiterm fractional differential equations using the matrix Mittag-Leffler functions. Mathematics 6(1):1–7

    MathSciNet  MATH  Google Scholar 

  38. Garrappa R (2018) Numerical solution of fractional differential equations: a survey and a software tutorial. Mathematics 6(2):1–16

    MATH  Google Scholar 

  39. Solís-Pérez JE, Gómez-Aguilar JF, Atangana A (2018) Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals 116:114–120

    MathSciNet  MATH  Google Scholar 

  40. Samko SG (1995) Fractional integration and differentiation of variable order. Anal Math 21(3):213–236

    MathSciNet  MATH  Google Scholar 

  41. Samko S (2013) Fractional integration and differentiation of variable order: an overview. Nonlinear Dyn 71(4):653–662

    MathSciNet  MATH  Google Scholar 

  42. Malesza W, Macias M, Sierociuk D (2019) Analytical solution of fractional variable order differential equations. J Comput Appl Math 348:214–236

    MathSciNet  MATH  Google Scholar 

  43. Sun H, Chang A, Zhang Y, Chen W (2019) A review on variable-order fractional differential equations: mathematical foundations, physical models, numerical methods and applications. Fract Calc Appl Anal 22(1):27–59

    MathSciNet  MATH  Google Scholar 

  44. Garrappa R, Popolizio M (2011) On accurate product integration rules for linear fractional differential equations. J Comput Appl Math 235(5):1085–1097

    MathSciNet  MATH  Google Scholar 

  45. Sheu LJ, Chen HK, Chen JH, Tam LM, Chen WC, Lin KT, Kang Y (2008) Chaos in the Newton-Leipnik system with fractional order. Chaos Solitons Fractals 36(1):98–103

    MathSciNet  MATH  Google Scholar 

  46. Luo X, Small M, Danca MF, Chen G (2007) On a dynamical system with multiple chaotic attractors. Int J Bifurc Chaos 17(09):3235–3251

    MathSciNet  MATH  Google Scholar 

  47. Dadras S, Momeni HR, Qi G (2010) Analysis of a new 3D smooth autonomous system with different wing chaotic attractors and transient chaos. Nonlinear Dyn 62(1–2):391–405

    MathSciNet  MATH  Google Scholar 

  48. Aizawa Y (1982) Global Aspects of the Dissipative Dynamical Systems I: Statistical Identification and Fractal Properties of the Lorenz Chaos. Progress Theoret Phys 68(1):64–84

    MathSciNet  MATH  Google Scholar 

  49. Thomas R (1999) Deterministic chaos seen in terms of feedback circuits: Analysis, synthesis, labyrinth chaos. Int J Bifurc Chaos 9(10):1889–1905

    MathSciNet  MATH  Google Scholar 

  50. En-Zeng D, Zai-Ping C, Zeng-Qiang C, Zhu-Zhi Y (2009) A novel four-wing chaotic attractor generated from a three-dimensional quadratic autonomous system. Chin Phys B 18(7):1–16

    Google Scholar 

Download references

Acknowledgements

José Francisco Gómez Aguilar acknowledges the support provided by CONACyT: cátedras CONACyT para jóvenes investigadores 2014 and SNI-CONACyT.

Author information

Authors and Affiliations

  1. Department of Engineering Science, Kermanshah University of Technology, Kermanshah, Iran

    Behzad Ghanbari

  2. Department of Mathematics, Faculty of Engineering and Natural Sciences, Bahcesehir University, 34349, Istanbul, Turkey

    Behzad Ghanbari

  3. CONACyT-Tecnológico Nacional de México/CENIDET., Interior Internado Palmira S/N, Col. Palmira, C.P. 62490, Cuernavaca, Morelos, Mexico

    J. F. Gómez-Aguilar

Authors
  1. Behzad Ghanbari
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. J. F. Gómez-Aguilar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to J. F. Gómez-Aguilar.

Ethics declarations

Conflicts of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghanbari, B., Gómez-Aguilar, J.F. Two efficient numerical schemes for simulating dynamical systems and capturing chaotic behaviors with Mittag–Leffler memory. Engineering with Computers 38, 2139–2167 (2022). https://doi.org/10.1007/s00366-020-01170-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01170-0

Keywords