Skip to main content
Springer Nature Link
Log in

Numerical thermoelastic eigenfrequency prediction of damaged layered shell panel with concentric/eccentric cutout and corrugated (TD/TID) properties

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

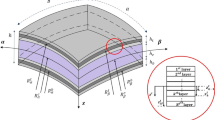
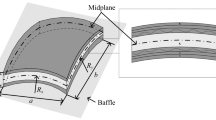
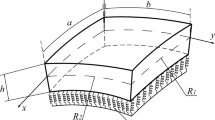
The vibrational responses are predicted numerically for the layered shell panel structure with and without cutout under the variable temperature loading and corrugated composite properties. The presence of variable cutout shapes (circular/elliptical/square and rectangular) and sizes are modelled via a generic mathematical macro-mechanical model in the framework of the cubic-order kinematic model. Also, the present model includes the variation of composite properties due to the change in environmental conditions, i.e. the temperature-dependent (TD) and -independent (TID) cases. The computational responses are obtained by taking advantages of the isoparametric finite element technique and the Hamilton principle to derive the final governing equation. The total Lagrangian approach is adopted to compute the responses using the specialized computer code prepared in the MATLAB platform. The frequency responses are predicted considering the effect of a cutout, including the environmental variation and compared with previously published eigenvalues. The model versatility is tested over a variety of examples considering the shell configurations (plate, cylindrical, spherical, hyperboloid, and elliptical), the influential cutout parameter (shape, size, and position) and temperature loading including the corrugated composite properties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Abbreviations

\(n\) :

Number of layers in the laminated shell panel

\(\theta\) :

Angle of fibre orientation

\(\left[ H \right]\) :

Thickness of coordinate matrix

\(\left\{ \sigma \right\}\) :

Stress

\(\left[ {\overline{Q}} \right]\) :

Reduced transformed elastic constant matrix

\(\varepsilon\) :

Strain

\(\alpha\) :

Thermal expansion coefficient

\(\Delta T\) :

Temperature difference

\(S\) :

Strain energy

\(T\) :

Kinetic energy

\(\left[ M \right]\) :

Mass matrix

\(\rho\) :

Mass density

\(N\) :

Shape function

\(\left[ K \right]\) :

Stiffness matrix

\(\left\{ \Phi \right\}\) :

Eigenvector

\(\omega\) :

Natural frequency

\(\omega_{{{\text{nd}}}}\) :

Normalized natural frequency

\(E_{1} ,\,E_{2} \,{\text{and}}\,E_{3}\) :

Young’s modulus

\(G_{12} ,\,G_{13} \,{\text{and}}\,G_{23}\) :

Shear modulus

\(\mu_{12} ,\,\mu_{13} \,{\text{and}}\,\mu_{23}\) :

Poisson’s ratio

\(\left[ {K_{{\text{G}}} } \right]\) :

Geometrical stiffness matrix

\(u_{{0\zeta_{x} }} ,\,\,u_{{0\zeta_{y} }}\) and \(u_{{0\zeta_{z} }} \,\) :

Displacement of a point at mid-plane

\(u_{{1\zeta_{y} }}\) and \(u_{{1\zeta_{x} }}\) :

Rotation along \(\zeta_{y}\) and \(\zeta_{y}\)

\(R_{{\zeta_{x} }}\), \(R_{{\zeta_{y} }}\) and \(R_{{\zeta_{xy} }}\) :

Radius of curvature of the shell panel

\(\zeta_{x}\), \(\zeta_{y}\) and \(\zeta_{z}\) :

Global reference axis of the laminate’s shell panel

\(\left[ D \right]\) and \(\left[ {D_{{\text{G}}} } \right]\) :

Material property matrix

\(\left[ {B_{{\text{l}}} } \right]\) and \(\left[ {B_{{\text{G}}} } \right]\) :

Strain displacement matrix

\(L,\,W\)and \(h\) :

Length, width and thickness of the shell panel

\(U_{{\zeta_{x} }} ,\,U_{{\zeta_{y} }}\) and \(U_{{\zeta_{z} }}\) :

Global displacement

\(u_{{2\zeta_{x} }} ,\,\,u_{{2\zeta_{y} }} ,\,\,u_{{3\zeta_{x} }} \,\,\) and \(u_{{3\zeta_{y} }}\) :

Higher-order deformation parameters

\(\left\{ \lambda \right\},\left\{ {\dot{\lambda }} \right\}\) and \(\left\{ {\ddot{\lambda }} \right\}\) :

Displacement, velocity and acceleration

\(\left\{ {\lambda_{0} } \right\}\) and \(\left\{ {\lambda_{0i} } \right\}\) :

Elemental and nodal displacement

\(A^{\prime}\) and \(A\) :

Area of the cutout and laminated shell panel

t :

Time

References

  1. Farokhian A, Kolahchi R (2020) Frequency and instability responses in nanocomposite plate assuming different distribution of CNTs. Struct Eng Mech 73:555–563. https://doi.org/10.12989/sem.2020.73.5.555

    Article  Google Scholar 

  2. Keshtegar B, Motezaker M, Kolahchi R, Trung N-T (2020) Wave propagation and vibration responses in porous smart nanocomposite sandwich beam resting on Kerr foundation considering structural damping. Thin Walled Struct 154:106820. https://doi.org/10.1016/j.tws.2020.106820

    Article  Google Scholar 

  3. Kolahchi R, Hosseini H, Fakhar MH et al (2019) A numerical method for magneto-hygro-thermal postbuckling analysis of defective quadrilateral graphene sheets using higher order nonlocal strain gradient theory with different movable boundary conditions. Comput Math Appl 78:2018–2034. https://doi.org/10.1016/j.camwa.2019.03.042

    Article  MathSciNet  MATH  Google Scholar 

  4. Keshtegar B, Tabatabaei J, Kolahchi R, Nguyen-Thoi T (2020) Dynamic stress response in the nanocomposite concrete pipes with internal fluid under the ground motion load. Adv Civ Eng 9:327–335. https://doi.org/10.12989/acc.2020.9.3.327

    Article  Google Scholar 

  5. Taherifar R, Zareei SA, Bidgoli MR, Kolahchi R (2021) Application of differential quadrature and Newmark methods for dynamic response in pad concrete foundation covered by piezoelectric layer. J Comput Appl Math 382:113075. https://doi.org/10.1016/j.cam.2020.113075

    Article  MathSciNet  MATH  Google Scholar 

  6. Motezaker M, Jamali M, Kolahchi R (2020) Application of differential cubature method for nonlocal vibration, buckling and bending response of annular nanoplates integrated by piezoelectric layers based on surface-higher order nonlocal-piezoelasticity theory. J Comput Appl Math 369:112625. https://doi.org/10.1016/j.cam.2019.112625

    Article  MathSciNet  MATH  Google Scholar 

  7. Wu L (2006) Thermal vibration analysis of thick laminated plates by the moving least squares differential quadrature method. Struct Eng Mech 22:331–349. https://doi.org/10.12989/sem.2006.22.3.331

    Article  Google Scholar 

  8. Kalita K, Dey P, Haldar S, Gao X-Z (2020) Optimizing frequencies of skew composite laminates with metaheuristic algorithms. Eng Comput 36:741–761. https://doi.org/10.1007/s00366-019-00728-x

    Article  Google Scholar 

  9. Khiloun M, Bousahla AA, Kaci A et al (2020) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT. Eng Comput 36:807–821. https://doi.org/10.1007/s00366-019-00732-1

    Article  Google Scholar 

  10. Menasria A, Kaci A, Bousahla AA, Bourada F et al (2020) A four-unknown refined plate theory for dynamic analysis of FG-sandwich plates under various boundary conditions. Steel Compos Struct 36:355–367. https://doi.org/10.12989/scs.2020.36.3.355

    Article  Google Scholar 

  11. Chikr SC, Kaci A, Bousahla AA et al (2020) A novel four-unknown integral model for buckling response of FG sandwich plates resting on elastic foundations under various boundary conditions using Galerkin’s approach. Geomech Eng 21:471–487. https://doi.org/10.12989/GAE.2020.21.5.471

    Article  Google Scholar 

  12. Rahmani MC, Kaci A, Bousahla AA et al (2020) Influence of boundary conditions on the bending and free vibration behavior of FGM sandwich plates using a four-unknown refined integral plate theory. Comput Concr 25:225–244. https://doi.org/10.12989/cac.2020.25.3.225

    Article  Google Scholar 

  13. Addou FY, Meradjah M, Bousahla AA et al (2019) Influences of porosity on dynamic response of FG plates resting on Winkler/Pasternak/Kerr foundation using quasi 3D HSDT. Comput Concr 24:347–367. https://doi.org/10.12989/cac.2019.24.4.347

    Article  Google Scholar 

  14. Belbachir N, Bourada M, Draiche K et al (2020) Thermal flexural analysis of anti-symmetric cross-ply laminated plates using a four variable refined theory. Smart Struct Syst 25:409–422. https://doi.org/10.12989/sss.2020.25.4.409

    Article  Google Scholar 

  15. Tounsi A, Al-Dulaijan SU, Al-Osta MA et al (2020) A four variable trigonometric integral plate theory for hygro-thermo-mechanical bending analysis of AFG ceramic-metal plates resting on a two-parameter elastic foundation. Steel Compos Struct 34:511–524. https://doi.org/10.12989/scs.2020.34.4.511

    Article  Google Scholar 

  16. Abualnour M, Chikh A, Hebali H et al (2019) Thermomechanical analysis of antisymmetric laminated reinforced composite plates using a new four variable trigonometric refined plate theory. Comput Concr 24:489–498. https://doi.org/10.12989/cac.2019.24.6.489

    Article  Google Scholar 

  17. Zarga D, Tounsi A, Bousahla AA et al (2019) Thermomechanical bending study for functionally graded sandwich plates using a simple quasi-3D shear deformation theory. Steel Compos Struct 32:389–410. https://doi.org/10.12989/scs.2019.32.3.389

    Article  Google Scholar 

  18. Mahmoudi A, Benyoucef S, Tounsi A et al (2019) A refined quasi-3D shear deformation theory for thermo-mechanical behavior of functionally graded sandwich plates on elastic foundations. J Sandw Struct Mater 21:1906–1929. https://doi.org/10.1177/1099636217727577

    Article  Google Scholar 

  19. Patel BP, Ganapathi M, Makhecha DP (2002) Hygrothermal effects on the structural behaviour of thick composite laminates using higher-order theory. Compos Struct 56:25–34. https://doi.org/10.1016/S0263-8223(01)00182-9

    Article  Google Scholar 

  20. Hajmohammad MH, Nouri AH, Zarei MS, Kolahchi R (2019) A new numerical approach and visco-refined zigzag theory for blast analysis of auxetic honeycomb plates integrated by multiphase nanocomposite facesheets in hygrothermal environment. Eng Comput 35:1141–1157. https://doi.org/10.1007/s00366-018-0655-x

    Article  Google Scholar 

  21. Azmi M, Kolahchi R, Bidgoli MR (2019) Dynamic analysis of concrete column reinforced with Sio2 nanoparticles subjected to blast load. Adv Concr Constr 7:51–63. https://doi.org/10.12989/acc.2019.7.1.051

    Article  Google Scholar 

  22. Shen H, Zheng J-J, Huang X-L (2003) Dynamic response of shear deformable laminated plates under thermomechanical loading and resting on elastic foundations. Compos Struct 60:57–66. https://doi.org/10.1016/S0263-8223(02)00295-7

    Article  Google Scholar 

  23. Mahi A, Adda Bedia EA, Tounsi A, Mechab I (2010) An analytical method for temperature-dependent free vibration analysis of functionally graded beams with general boundary conditions. Compos Struct 92:1877–1887. https://doi.org/10.1016/j.compstruct.2010.01.010

    Article  Google Scholar 

  24. Lal A, Singh BN (2010) Stochastic free vibration of laminated composite plates in thermal environments. J Thermoplast Compos Mater 23:57–77. https://doi.org/10.1177/0892705708103399

    Article  Google Scholar 

  25. Bui TQ, Van DT, Ton LHT et al (2016) On the high temperature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos Part B Eng 92:218–241. https://doi.org/10.1016/j.compositesb.2016.02.048

    Article  Google Scholar 

  26. Szekrényes A (2015) A special case of parametrically excited systems: free vibration of delaminated composite beams. Eur J Mech A Solids 49:82–105. https://doi.org/10.1016/j.euromechsol.2014.07.003

    Article  MathSciNet  MATH  Google Scholar 

  27. Juhász Z, Szekrényes A (2020) An analytical solution for buckling and vibration of delaminated composite spherical shells. Thin Walled Struct 148:106563. https://doi.org/10.1016/j.tws.2019.106563

    Article  Google Scholar 

  28. Szekrényes A (2014) Coupled flexural–longitudinal vibration of delaminated composite beams with local stability analysis. J Sound Vib 333:5141–5164. https://doi.org/10.1016/j.jsv.2014.05.021

    Article  Google Scholar 

  29. Nguyen LB, Thai CH, Nguyen-Xuan H (2016) A generalized unconstrained theory and isogeometric finite element analysis based on Bézier extraction for laminated composite plates. Eng Comput 32:457–475. https://doi.org/10.1007/s00366-015-0426-x

    Article  Google Scholar 

  30. Naidu NVS, Sinha PK (2007) Nonlinear free vibration analysis of laminated composite shells in hygrothermal environments. Compos Struct 77:475–483. https://doi.org/10.1016/j.compstruct.2005.08.002

    Article  Google Scholar 

  31. Panda HS, Sahu SK, Parhi PK (2013) Hygrothermal effects on free vibration of delaminated woven fiber composite plates—numerical and experimental results. Compos Struct 96:502–513. https://doi.org/10.1016/j.compstruct.2012.08.057

    Article  Google Scholar 

  32. Rath M, Sahu S (2012) Vibration of woven fiber laminated composite plates in hygrothermal environment. J Vib Control 18:1957–1970. https://doi.org/10.1177/1077546311428638

    Article  Google Scholar 

  33. Asadi H, Bodaghi M, Shakeri M, Aghdam MM (2013) On the free vibration of thermally pre/post-buckled shear deformable SMA hybrid composite beams. Aerosp Sci Technol 31:73–86. https://doi.org/10.1016/j.ast.2013.09.008

    Article  Google Scholar 

  34. Nanda N, Pradyumna S (2011) Nonlinear dynamic response of laminated shells with imperfections in hygrothermal environments. J Compos Mater 45:2103–2112. https://doi.org/10.1177/0021998311401061

    Article  Google Scholar 

  35. Asadi H, Aghdam MM (2014) Large amplitude vibration and post-buckling analysis of variable cross-section composite beams on nonlinear elastic foundation. Int J Mech Sci 79:47–55. https://doi.org/10.1016/j.ijmecsci.2013.11.017

    Article  Google Scholar 

  36. Al-Furjan MSH, Safarpour H, Habibi M et al (2020) A comprehensive computational approach for nonlinear thermal instability of the electrically FG-GPLRC disk based on GDQ method. Eng Comput. https://doi.org/10.1007/s00366-020-01088-7

    Article  Google Scholar 

  37. Al-Furjan MSH, Habibi M, Chen G et al (2020) Chaotic oscillation of a multi-scale hybrid nano-composites reinforced disk under harmonic excitation via GDQM. Compos Struct 252:112737. https://doi.org/10.1016/j.compstruct.2020.112737

    Article  Google Scholar 

  38. Shariati A, Ghabussi A, Habibi M et al (2020) Extremely large oscillation and nonlinear frequency of a multi-scale hybrid disk resting on nonlinear elastic foundation. Thin Walled Struct 154:106840. https://doi.org/10.1016/j.tws.2020.106840

    Article  Google Scholar 

  39. Al-Furjan MSH, Habibi M, Rahimi A et al (2020) Chaotic simulation of the multi-phase reinforced thermo-elastic disk using GDQM. Eng Comput. https://doi.org/10.1007/s00366-020-01144-2

    Article  Google Scholar 

  40. Keshtegar B, Farrokhian A, Kolahchi R, Trung N-T (2020) Dynamic stability response of truncated nanocomposite conical shell with magnetostrictive face sheets utilizing higher order theory of sandwich panels. Eur J Mech A Solids 82:104010. https://doi.org/10.1016/j.euromechsol.2020.104010

    Article  MathSciNet  MATH  Google Scholar 

  41. Malekzadeh P, Hamzehkolaei NS (2013) A 3D discrete layer-differential quadrature free vibration of multi-layered FG annular plates in thermal environment. Mech Adv Mater Struct 20:316–330. https://doi.org/10.1080/15376494.2011.627637

    Article  Google Scholar 

  42. Malekzadeh P, Bahranifard F, Ziaee S (2013) Three-dimensional free vibration analysis of functionally graded cylindrical panels with cut-out using Chebyshev–Ritz method. Compos Struct 105:1–13. https://doi.org/10.1016/j.compstruct.2013.05.005

    Article  Google Scholar 

  43. Natarajan S, Deogekar PS, Manickam G, Belouettar S (2014) Hygrothermal effects on the free vibration and buckling of laminated composites with cutouts. Compos Struct 108:848–855. https://doi.org/10.1016/j.compstruct.2013.10.009

    Article  Google Scholar 

  44. Venkatachari A, Natarajan S, Haboussi M, Ganapathi M (2016) Environmental effects on the free vibration of curvilinear fibre composite laminates with cutouts. Compos Part B Eng 88:131–138. https://doi.org/10.1016/j.compositesb.2015.10.017

    Article  Google Scholar 

  45. Ram KSS, Sinha PK (1992a) Hygrothermal effects on the free vibration of laminated composite plates. J Sound Vib 158:133–148. https://doi.org/10.1016/0022-460X(92)90669-O

    Article  MATH  Google Scholar 

  46. Ram KSS, Sinha PK (1991) Hygrothermal effects on the bending characteristics of laminated composite plates. Comput Struct 40:1009–1015. https://doi.org/10.1016/0045-7949(91)90332-G

    Article  Google Scholar 

  47. Ram KSS, Sinha PK (1992b) Hygrothermal bending of laminated composite plates with a cutout. Comput Struct 43:1105–1115. https://doi.org/10.1016/0045-7949(92)90011-N

    Article  Google Scholar 

  48. Barut A, Madenci E (2004) Thermomechanical stress analysis of laminates with a cutout via a complex potential-variational method. J Therm Stress 27:1–31. https://doi.org/10.1080/01495730490255691

    Article  Google Scholar 

  49. Ganesan N, Kadoli R (2004) Studies on linear thermoelastic buckling and free vibration analysis of geometrically perfect hemispherical shells with cut-out. J Sound Vib 277:855–879. https://doi.org/10.1016/j.jsv.2003.09.008

    Article  Google Scholar 

  50. Kadoli R, Ganesan N (2005) A theoretical analysis of linear thermoelastic buckling of composite hemispherical shells with a cut-out at the apex. Compos Struct 68:87–101. https://doi.org/10.1016/j.compstruct.2004.03.003

    Article  Google Scholar 

  51. Shaterzadeh AR, Abolghasemi S, Rezaei R (2014) Finite element analysis of thermal buckling of rectangular laminated composite plates with circular cut-out. J Therm Stress 37:604–623. https://doi.org/10.1080/01495739.2014.885322

    Article  Google Scholar 

  52. Darvizeh M, Darvizeh A, Shaterzadeh AR, Ansari R (2010) Thermal buckling of spherical shells with cut-out. J Therm Stress 33:441–458. https://doi.org/10.1080/01495731003738432

    Article  Google Scholar 

  53. Rahimabadi AA, Natarajan S, Bordas SP (2013) Vibration of functionally graded material plates with cutouts and cracks in thermal environment. Key Eng Mater 560:157–180. https://doi.org/10.4028/www.scientific.net/KEM.560.157

    Article  Google Scholar 

  54. Janghorban M, Zare A (2011) Thermal effect on free vibration analysis of functionally graded arbitrary straight-sided plates with different cutouts. Lat Am J Solids Struct 8:245–257. https://doi.org/10.1590/S1679-78252011000300003

    Article  Google Scholar 

  55. Dewangan HC, Katariya PV, Panda SK (2020) Time-dependent transverse deflection responses of the layered composite plate with concentric circular cut-out. Mater Today Proc. https://doi.org/10.1016/j.matpr.2020.02.825

    Article  Google Scholar 

  56. Hirwani CK, Panda SK (2019) Nonlinear thermal free vibration frequency analysis of delaminated shell panel using FEM. Compos Struct 224:111011. https://doi.org/10.1016/j.compstruct.2019.111011

    Article  Google Scholar 

  57. Sahoo SS, Panda SK, Sen D (2016) Effect of delamination on static and dynamic behavior of laminated composite plate. AIAA J 54:2530–2544. https://doi.org/10.2514/1.J054908

    Article  Google Scholar 

  58. Hirwani CK, Panda SK, Mahapatra TR, Mahapatra SS (2017) Nonlinear transient finite-element analysis of delaminated composite shallow shell panels. AIAA J 55:1734–1748. https://doi.org/10.2514/1.J055624

    Article  Google Scholar 

  59. Kar VR, Panda SK (2017) Large-amplitude vibration of functionally graded doubly-curved panels under heat conduction. AIAA J 55:4376–4386. https://doi.org/10.2514/1.J055878

    Article  Google Scholar 

  60. Cook RD, Malkus DS, Plesha ME, Witt RJ (2002) Concepts and applications of finite element analysis, fourth. Wiley, New York

    Google Scholar 

  61. Ramakrishna S, Rao KM, Rao NS (1992) Free vibration analysis of laminates with circular cutout by hybrid-stress finite element. Compos Struct 21:177–185. https://doi.org/10.1016/0263-8223(92)90017-7

    Article  Google Scholar 

  62. Chen L-W, Chen L-Y (1991) Thermal postbuckling behaviors of laminated composite plates with temperature-dependent properties. Compos Struct 19:267–283. https://doi.org/10.1016/0263-8223(91)90031-S

    Article  Google Scholar 

  63. Yüksel YZ, Akbaş ŞD (2018) Free vibration analysis of a cross-ply laminated plate in thermal environment. Int J Eng Appl Sci 10:176–189. https://doi.org/10.24107/ijeas.456755

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology Rourkela, Rourkela, 769008, Odisha, India

    Hukum Chand Dewangan & Subrata Kumar Panda

Authors
  1. Hukum Chand Dewangan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Subrata Kumar Panda
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Subrata Kumar Panda.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dewangan, H.C., Panda, S.K. Numerical thermoelastic eigenfrequency prediction of damaged layered shell panel with concentric/eccentric cutout and corrugated (TD/TID) properties. Engineering with Computers 38, 2009–2025 (2022). https://doi.org/10.1007/s00366-020-01199-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01199-1

Keywords