Abstract
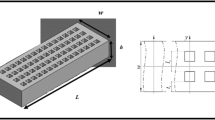
Perforated beam is essential structural element of Nano-Electro-Mechanical-Systems (NEMS), whose design needs appropriate modelling of size of holes, hole numbers, and scale effects. The current manuscript presents a comprehensive study and develops non-classical closed form solutions to predict the static bending behavior and buckling stability of perforated nanobeams (PNBs) incorporating the surface energy for different four beams theories, for the first time. Equivalent geometrical models for both bulk and surface characteristics are presented. The Gurtin–Murdoch surface elasticity model is modified and adopted to include the perforation in surface characteristics. To consider the warping shear effect on bending as well as critical buckling loads with the presence of surface stress effects, four different beams theories with shear deformation are considered. The non-classical equilibrium equations relevant to each PNB theory are developed in detail. Closed-form solutions are developed considering the different classical and non-classical boundary conditions as well as loading conditions. The proposed methodology is verified by comparing the obtained results with the available analytical solutions for fully filled beams and excellent agreement is observed. Effects of perforation characteristics as well as the surface effects on bending and buckling behaviors are investigated.


Similar content being viewed by others
References
Abdelrahman AA, Eltaher MA, Kabeel AM, Abdraboh AM, Hendi AA (2019) Free and forced analysis of perforated beams. Steel Compos Struct 31(5):489–502. https://doi.org/10.12989/scs.2019.31.5.489
Agwa MA, Eltaher MA (2016) Vibration of a carbyne nanomechanical mass sensor with surface effect. Appl Phys A 122(4):335. https://doi.org/10.1007/s00339-016-9934-9
Akbaş ŞD (2016) Static analysis of a nano plate by using generalized differential quadrature method. Int J Eng Appl Sci 8(2):30–39
Akbaş ŞD (2017) Free vibration of edge cracked functionally graded microscale beams based on the modified couple stress theory. Int J Struct Stab Dyn 17(03):1750033. https://doi.org/10.1142/S021945541750033X
Akbaş ŞD (2018a) Forced vibration analysis of cracked nanobeams. J Braz Soc Mech Sci Eng 40(8):392. https://doi.org/10.1007/s40430-018-1315-1
Akbaş ŞD (2018b) Bending of a cracked functionally graded nanobeam. Adv Nano Res 6(3):219. https://doi.org/10.12989/anr.2018.6.3.219
Akbaş ŞD (2019a) Longitudinal forced vibration analysis of porous a nanorod. Mühendislik Bilimleri ve Tasarım Dergisi 7(4):736–743. https://doi.org/10.21923/jesd.553328
Akbaş ŞD (2019b) Axially forced vibration analysis of cracked a nanorod. J Comput Appl Mech 50(1):63–68
Akbas SD (2020) Modal analysis of viscoelastic nanorods under an axially harmonic load. Adv Nano Res 8(4):277–282. https://doi.org/10.12989/anr.2020.8.4.277
Akgöz B, Civalek Ö (2016) Bending analysis of embedded carbon nanotubes resting on an elastic foundation using strain gradient theory. Acta Astronaut 119:1–12. https://doi.org/10.1016/j.actaastro.2015.10.021
Allahyari E, Asgari M (2019) Thermo-mechanical vibration of double-layer graphene nanosheets in elastic medium considering surface effects; developing a nonlocal third order shear deformation theory. Eur J Mech A/Solids 75:307–321. https://doi.org/10.1016/j.euromechsol.2019.01.022
Almitani KH, Abdelrahman AA, Eltaher MA (2019) On forced and free vibrations of cutout squared beams. Steel Compos Struct 32(5):643–655. https://doi.org/10.12989/scs.2019.32.5.643
Almitani KH, Abdelrahman AA, Eltaher MA (2020) Stability of PNBs incorporating surface energy effects. Steel Compos Struct 35(4):555–566. https://doi.org/10.12989/scs.2020.35.4.555
Ansari R, Sahmani S (2011) Bending behavior and buckling of nanobeams including surface stress effects corresponding to different beam theories. Int J Eng Sci 49(11):1244–1255. https://doi.org/10.1016/j.ijengsci.2011.01.007
Apuzzo A, Barretta R, Faghidian SA, Luciano R, De Sciarra FM (2019) Nonlocal strain gradient exact solutions for functionally graded inflected nano-beams. Compos B Eng 164:667–674. https://doi.org/10.1016/j.compositesb.2018.12.112
Apuzzo A, Barretta R, Fabbrocino F, Faghidian SA, Luciano R, Marotti de Sciarra F (2019) Axial and torsional free vibrations of elastic nano-beams by stress-driven two-phase elasticity. J Appl Comput Mech 5(2):402–413. https://doi.org/10.22055/jacm.2018.26552.1338
Attia MA, Rahman AAA (2018) On vibrations of functionally graded viscoelastic nanobeams with surface effects. Int J Eng Sci 127:1–32. https://doi.org/10.1016/j.ijengsci.2018.02.005
Baghdadi H, Tounsi A, Zidour M, Benzair A (2015) Thermal effect on vibration characteristics of armchair and zigzag single-walled carbon nanotubes using nonlocal parabolic beam theory. Fullerenes Nanotubes Carbon Nanostruct 23(3):266–272. https://doi.org/10.1080/1536383X.2013.787605
Barretta R, Čanađija M, Luciano R, de Sciarra FM (2018) Stress-driven modeling of nonlocal thermoelastic behavior of nanobeams. Int J Eng Sci 126:53–67. https://doi.org/10.1016/j.ijengsci.2018.02.012
Barretta R, Luciano R, de Sciarra FM, Ruta G (2018) Stress-driven nonlocal integral model for Timoshenko elastic nano-beams. Eur J Mech A/Solids 72:275–286. https://doi.org/10.1016/j.euromechsol.2018.04.012
Barretta R, Faghidian SA, Luciano R, Medaglia CM, Penna R (2018) Free vibrations of FG elastic Timoshenko nano-beams by strain gradient and stress-driven nonlocal models. Compos B Eng 154:20–32. https://doi.org/10.1016/j.compositesb.2018.07.036
Barretta R, de Sciarra FM, Vaccaro MS (2019) On nonlocal mechanics of curved elastic beams. Int J Eng Sci 144:103140. https://doi.org/10.1016/j.ijengsci.2019.103140
Barretta R, Faghidian SA, de Sciarra FM (2019) Stress-driven nonlocal integral elasticity for axisymmetric nano-plates. Int J Eng Sci 136:38–52. https://doi.org/10.1016/j.ijengsci.2019.01.003
Barretta R, de Sciarra FM (2019) Variational nonlocal gradient elasticity for nano-beams. Int J Eng Sci 143:73–91. https://doi.org/10.1016/j.ijengsci.2019.06.016
Barretta R, Faghidian SA, de Sciarra FM, Pinnola FP (2020) On nonlocal Lam strain gradient mechanics of elastic rods. Int J Multiscale Comput Eng. https://doi.org/10.1615/IntJMultCompEng.2019030655
Bedia WA, Houari MSA, Bessaim A, Bousahla AA, Tounsi A, Saeed T, Alhodaly MS (2019) A new hyperbolic two-unknown beam model for bending and buckling analysis of a nonlocal strain gradient nanobeams. J Nano Res 57:175–191. https://doi.org/10.4028/www.scientific.net/JNanoR.57.175
Bendali A, Labedan R, Domingue F, Nerguizian V (2006) Holes effects on RF MEMS parallel membranes capacitors. In 2006 Canadian Conference on Electrical and Computer Engineering (pp. 2140–2143). IEEE. https://doi.org/10.1109/CCECE.2006.277600
Bessaim A, Houari MSA, Bernard F, Tounsi A (2015) A nonlocal quasi-3D trigonometric plate model for free vibration behaviour of micro/nanoscale plates. Struct Eng Mech 56(2):223–240. https://doi.org/10.12989/sem.2015.56.2.223
Bourouina H, Yahiaoui R, Sahar A, Benamar MEA (2016) Analytical modeling for the determination of nonlocal resonance frequencies of PNBs subjected to temperature-induced loads. Phys E 75:163–168. https://doi.org/10.1016/j.physe.2015.09.014
Bourouina H, Yahiaoui R, Kerid R, Ghoumid K, Lajoie I, Picaud F, Herlem G (2020) The influence of hole networks on the adsorption-induced frequency shift of a PNB using non-local elasticity theory. J Phys Chem Solids 136:109201. https://doi.org/10.1016/j.jpcs.2019.109201
Civalek Ö, Demir Ç (2011) Bending analysis of microtubules using nonlocal Euler–Bernoulli beam theory. Appl Math Model 35(5):2053–2067. https://doi.org/10.1016/j.apm.2010.11.004
Daikh AA, Drai A, Houari MSA, Eltaher MA (2020) Static analysis of multilayer nonlocal strain gradient nanobeam reinforced by carbon nanotubes. Steel Compos Struct 36(6):643–656. https://doi.org/10.12989/scs.2020.36.6.643
Daikh AA, Bachiri A, Houari MSA, Tounsi A (2020) Size dependent free vibration and buckling of multilayered carbon nanotubes reinforced composite nanoplates in thermal environment. Mech Based Des Struct Mach. https://doi.org/10.1080/15397734.2020.1752232
De Pasquale G, Veijola T, Somà A (2009) Modelling and validation of air damping in perforated gold and silicon MEMS plates. J Micromech Microeng 20(1):015010. https://doi.org/10.1088/0960-1317/20/1/015010
Demir Ç, Civalek Ö (2017) On the analysis of microbeams. Int J Eng Sci 121:14–33. https://doi.org/10.1016/j.ijengsci.2017.08.016
Ebrahimi F, Barati MR (2017) A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams. Compos Struct 159:174–182. https://doi.org/10.1016/j.compstruct.2016.09.058
Ebrahimi F, Barati MR (2018) Vibration analysis of piezoelectrically actuated curved nanosize FG beams via a nonlocal strain-electric field gradient theory. Mech Adv Mater Struct 25(4):350–359. https://doi.org/10.1080/15376494.2016.1255830
Eltaher MA, Emam SA, Mahmoud FF (2012) Free vibration analysis of functionally graded size-dependent nanobeams. Appl Math Comput 218(14):7406–7420. https://doi.org/10.1016/j.amc.2011.12.090
Eltaher MA, Emam SA, Mahmoud FF (2013) Static and stability analysis of nonlocal functionally graded nanobeams. Compos Struct 96:82–88. https://doi.org/10.1016/j.compstruct.2012.09.030
Eltaher MA, Alshorbagy AE, Mahmoud FF (2013) Determination of neutral axis position and its effect on natural frequencies of functionally graded macro/nanobeams. Compos Struct 99:193–201. https://doi.org/10.1016/j.compstruct.2012.11.039
Eltaher MA, Mahmoud FF, Assie AE, Meletis EI (2013) Coupling effects of nonlocal and surface energy on vibration analysis of nanobeams. Appl Math Comput 224:760–774. https://doi.org/10.1016/j.amc.2013.09.002
Eltaher MA, Hamed MA, Sadoun AM, Mansour A (2014) Mechanical analysis of higher order gradient nanobeams. Appl Math Comput 229:260–272. https://doi.org/10.1016/j.amc.2013.12.076
Eltaher MA, Khairy A, Sadoun AM, Omar FA (2014) Static and buckling analysis of functionally graded Timoshenko nanobeams. Appl Math Comput 229:283–295. https://doi.org/10.1016/j.amc.2013.12.072
Eltaher MA, El-Borgi S, Reddy JN (2016) Nonlinear analysis of size-dependent and material-dependent nonlocal CNTs. Compos Struct 153:902–913. https://doi.org/10.1016/j.compstruct.2016.07.013
Eltaher MA, Agwa MA, Mahmoud FF (2016) Nanobeam sensor for measuring a zeptogram mass. Int J Mech Mater Des 12(2):211–221. https://doi.org/10.1007/s10999-015-9302-5
Eltaher MA, Khater ME, Emam SA (2016) A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Appl Math Model 40(5–6):4109–4128. https://doi.org/10.1016/j.apm.2015.11.026
Eltaher MA, Agwa M, Kabeel A (2018) Vibration analysis of material size-dependent CNTs using energy equivalent model. J Appl Comput Mech 4(2):75–86. https://doi.org/10.22055/JACM.2017.22579.1136
Eltaher MA, Kabeel AM, Almitani KH, Abdraboh AM (2018) Static bending and buckling of perforated nonlocal size-dependent nanobeams. Microsyst Technol 24(12):4881–4893. https://doi.org/10.1007/s00542-018-3905-3
Eltaher MA, Abdraboh AM, Almitani KH (2018) Resonance frequencies of size dependent perforated nonlocal nanobeam. Microsyst Technol 24(9):3925–3937. https://doi.org/10.1007/s00542-018-3910-6
Eltaher MA, Omar FA, Abdalla WS, Gad EH (2019) Bending and vibrational behaviors of piezoelectric nonlocal nanobeam including surface elasticity. Waves Random Complex Med 29(2):264–280. https://doi.org/10.1080/17455030.2018.1429693
Eltaher MA, Almalki TA, Ahmed KI, Almitani KH (2019) Characterization and behaviors of single walled carbon nanotube by equivalent-continuum mechanics approach. Adv Nano Res 7(1):39. https://doi.org/10.12989/anr.2019.7.1.039
Eltaher MA, Mohamed N, Mohamed S, Seddek LF (2019) Postbuckling of curved carbon nanotubes using energy equivalent model. J Nano Res 57:136–157. https://doi.org/10.4028/www.scientific.net/JNanoR.57.136
Eltaher MA, Almalki TA, Almitani KH, Ahmed KIE, Abdraboh AM (2019) Modal participation of fixed–fixed single-walled carbon nanotube with vacancies. Int J Adv Struct Eng 11(2):151–163. https://doi.org/10.1007/s40091-019-0222-8
Eltaher MA, Mohamed N (2020a) Nonlinear stability and vibration of imperfect CNTs by doublet mechanics. Appl Math Comput 382:125311. https://doi.org/10.1016/j.amc.2020.125311
Eltaher MA, Mohamed NA (2020b) Vibration of nonlocal PNBs with general boundary conditions. Smart Struct Syst 25(4):501–514. https://doi.org/10.12989/sss.2020.25.4.501
Eltaher MA, Mohamed N, Mohamed SA (2020) Nonlinear buckling and free vibration of curved CNTs by doublet mechanics. Smart Struct Syst 26(2):213–226. https://doi.org/10.12989/sss.2020.26.2.213
Eltaher MA, Omar FA, Abdraboh AM, Abdalla WS, Alshorbagy AE (2020) Mechanical behaviors of piezoelectric nonlocal nanobeam with cutouts. Smart Struct Syst 25(2):219–228. https://doi.org/10.12989/sss.2020.25.2.219
Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16. https://doi.org/10.1016/0020-7225(72)90070-5
Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710. https://doi.org/10.1063/1.332803
Ferrari M, Granik VT, Imam A, Nadeau JC (1997) Advances in doublet mechanics, vol 45. Springer Science & Business Media, Berlin
Gao G, Cagin T, Goddard WA III (1998) Energetics, structure, mechanical and vibrational properties of single-walled carbon nanotubes. Nanotechnology 9(3):184. https://doi.org/10.1088/0957-4484/9/3/007
Gao H, Huang Y, Nix WD, Hutchinson JW (1999) Mechanism-based strain gradient plasticity—I. Theory. J Mech Phys Solids 47(6):1239–1263. https://doi.org/10.1016/S0022-5096(98)00103-3
Guha K, Kumar M, Agarwal S, Baishya S (2015) A modified capacitance model of RF MEMS shunt switch incorporating fringing field effects of perforated beam. Solid-State Electron 114:35–42. https://doi.org/10.1016/j.sse.2015.07.008
Guha K, Laskar NM, Gogoi HJ, Borah AK, Baishnab KL, Baishya S (2017) Novel analytical model for optimizing the pull-in voltage in a flexured MEMS switch incorporating beam perforation effect. Solid-State Electron 137:85–94. https://doi.org/10.1016/j.sse.2017.08.007
Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech Anal 57(4):291–323. https://doi.org/10.1007/BF00261375
Gurtin ME, Murdoch AI (1978) Surface stress in solids. Int J Solids Struct 14(6):431–440
Hamed MA, Eltaher MA, Sadoun AM, Almitani KH (2016) Free vibration of symmetric and sigmoid functionally graded nanobeams. Appl Phys A 122(9):829. https://doi.org/10.1007/s00339-016-0324-0
Hamed MA, Sadoun AM, Eltaher MA (2019) Effects of porosity models on static behavior of size dependent functionally graded beam. Struct Eng Mech 71(1):89–98. https://doi.org/10.12989/sem.2019.71.1.089
Hamed MA, Mohamed NA, Eltaher MA (2020) Stability buckling and bending of nanobeams including cutouts. Eng Comput. https://doi.org/10.1007/s00366-020-01063-2
Hosseini-Hashemi S, Nazemnezhad R, Rokni H (2015) Nonlocal nonlinear free vibration of nanobeams with surface effects. Eur J Mech A/Solids 52:44–53. https://doi.org/10.1016/j.euromechsol.2014.12.012
Houari MSA, Bessaim A, Bernard F, Tounsi A, Mahmoud SR (2018) Buckling analysis of new quasi-3D FG nanobeams based on nonlocal strain gradient elasticity theory and variable length scale parameter. Steel Compos Struct 28(1):13–24. https://doi.org/10.12989/scs.2018.28.1.013
Jalaei MH, Arani AG, Nguyen-Xuan H (2019) Investigation of thermal and magnetic field effects on the dynamic instability of FG Timoshenko nanobeam employing nonlocal strain gradient theory. Int J Mech Sci 161:105043. https://doi.org/10.1016/j.ijmecsci.2019.105043
Jamalpoor A, Ahmadi-Savadkoohi A, Hosseini M, Hosseini-Hashemi S (2017) Free vibration and biaxial buckling analysis of double magneto-electro-elastic nanoplate-systems coupled by a visco-Pasternak medium via nonlocal elasticity theory. Eur J Mech A/Solids 63:84–98. https://doi.org/10.1016/j.euromechsol.2016.12.002
Kahrobaiyan MH, Asghari M, Rahaeifard M, Ahmadian MT (2011) A nonlinear strain gradient beam formulation. Int J Eng Sci 49(11):1256–1267. https://doi.org/10.1016/j.ijengsci.2011.01.006
Karami B, Janghorban M, Rabczuk T (2020) Dynamics of two-dimensional functionally graded tapered Timoshenko nanobeam in thermal environment using nonlocal strain gradient theory. Compos B Eng 182:107622. https://doi.org/10.1016/j.compositesb.2019.107622
Kerid R, Bourouina H, Yahiaoui R, Bounekhla M, Aissat A (2019) Magnetic field effect on nonlocal resonance frequencies of structure-based filter with periodic square holes network. Phys E 105:83–89. https://doi.org/10.1016/j.physe.2018.05.021
Khater ME, Eltaher MA, Abdel-Rahman E, Yavuz M (2014) Surface and thermal load effects on the buckling of curved nanowires. Eng Sci Technol Int J 17(4):279–283. https://doi.org/10.1016/j.jestch.2014.07.003
Khodabakhshi P, Reddy JN (2015) A unified integro-differential nonlocal model. Int J Eng Sci 95:60–75. https://doi.org/10.1016/j.ijengsci.2015.06.006
Koiter WT (1964) Couple stresses in the theory of elasticity. Proc Koninklijke Nederl Akaad van Wetensch. https://hal.archives-ouvertes.fr/hal-00852443
Kong S, Zhou S, Nie Z, Wang K (2009) Static and dynamic analysis of micro beams based on strain gradient elasticity theory. Int J Eng Sci 47(4):487–498. https://doi.org/10.1016/j.ijengsci.2008.08.008
Lam DC, Yang F, Chong ACM, Wang J, Tong P (2003) Experiments and theory in strain gradient elasticity. J Mech Phys Solids 51(8):1477–1508. https://doi.org/10.1016/S0022-5096(03)00053-X
Levinson M (1981) A new rectangular beam theory. J Sound Vib 74(1):81–87. https://doi.org/10.1016/0022-460X(81)90493-4
Li C, Chou TW (2003) A structural mechanics approach for the analysis of carbon nanotubes. Int J Solids Struct 40(10):2487–2499. https://doi.org/10.1016/S0020-7683(03)00056-8
Li L, Hu Y (2015) Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. Int J Eng Sci 97:84–94. https://doi.org/10.1016/j.ijengsci.2015.08.013
Li L, Lin R, Ng TY (2020) Contribution of nonlocality to surface elasticity. Int J Eng Sci 152:103311. https://doi.org/10.1016/j.ijengsci.2020.103311
Lim CW, Zhang G, Reddy JN (2015) A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids 78:298–313. https://doi.org/10.1016/j.jmps.2015.02.001
Liu H, Li B, Liu Y (2019) The inconsistency of nonlocal effect on carbon nanotube conveying fluid and a proposed solution based on local/nonlocal model. Eur J Mech A/Solids 78:103837. https://doi.org/10.1016/j.euromechsol.2019.103837
Liu Y, Wei Y (2020) Effect of surface energy on the indentation response of hard nanofilm/soft substrate composite structure. Int J Mech Sci. https://doi.org/10.1016/j.ijmecsci.2020.105759
Lu L, Guo X, Zhao J (2018) On the mechanics of Kirchhoff and Mindlin plates incorporating surface energy. Int J Eng Sci 124:24–40. https://doi.org/10.1016/j.ijengsci.2017.11.020
Luschi L, Pieri F (2014) An analytical model for the determination of resonance frequencies of perforated beams. J Micromech Microeng 24(5):055004. https://doi.org/10.1088/0960-1317/24/5/055004
Luschi L, Pieri F (2016) An analytical model for the resonance frequency of square perforated Lamé-mode resonators. Sens Actuators B Chem 222:1233–1239. https://doi.org/10.1016/j.snb.2015.07.085
Ma HM, Gao XL, Reddy JN (2008) A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J Mech Phys Solids 56(12):3379–3391. https://doi.org/10.1016/j.jmps.2008.09.007
Mahmoud FF, Eltaher MA, Alshorbagy AE, Meletis EI (2012) Static analysis of nanobeams including surface effects by nonlocal finite element. J Mech Sci Technol 26(11):3555–3563. https://doi.org/10.1007/s12206-012-0871-z
Malekzadeh P, Shojaee M (2013) Surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams. Compos B Eng 52:84–92. https://doi.org/10.1016/j.compositesb.2013.03.046
Malikan M (2019) On the buckling response of axially pressurized nanotubes based on a novel nonlocal beam theory. J Appl Comput Mech 5(1):103–112
Malikan M, Dimitri R, Tornabene F (2019) Transient response of oscillated carbon nanotubes with an internal and external damping. Compos B Eng 158:198–205. https://doi.org/10.1016/j.compositesb.2018.09.092
Malikan M (2020) On the plastic buckling of curved carbon nanotubes. Theor Appl Mech Lett 10(1):46–56. https://doi.org/10.1016/j.taml.2020.01.004
Malikan M, Eremeyev VA (2020a) On nonlinear bending study of a piezo-flexomagnetic nanobeam based on an analytical-numerical solution. Nanomaterials 10(9):1762. https://doi.org/10.3390/nano10091762
Malikan M, Eremeyev VA (2020b) On the dynamics of a visco–piezo–flexoelectric nanobeam. Symmetry 12(4):643. https://doi.org/10.3390/sym12040643
Malikan M, Eremeyev VA (2020c) Post-critical buckling of truncated conical carbon nanotubes considering surface effects embedding in a nonlinear Winkler substrate using the Rayleigh-Ritz method. Mater Res Exp 7(2):025005. https://doi.org/10.1088/2053-1591/ab691c
Merzouki T, Houari MSA, Haboussi M, Bessaim A, Ganapathi M (2020) Nonlocal strain gradient finite element analysis of nanobeams using two-variable trigonometric shear deformation theory. Eng Comput. https://doi.org/10.1007/s00366-020-01156-y
Malikan M, Eremeyev VA, Sedighi HM (2020) Buckling analysis of a non-concentric double-walled carbon nanotube. Acta Mech. https://doi.org/10.1007/s00707-020-02784-7
Malikan M, Uglov NS, Eremeyev VA (2020) On instabilities and post-buckling of piezomagnetic and flexomagnetic nanostructures. Int J Eng Sci 157:103395. https://doi.org/10.1016/j.ijengsci.2020.103395
Mindlin RD (1962) Influence of couple-stresses on stress concentrations. Columbia University, New york
Mindlin RD (1965) Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct 1(4):417–438. https://doi.org/10.1016/0020-7683(65)90006-5
Miller RE, Shenoy VB (2000) Size-dependent elastic properties of nanosized structural elements. Nanotechnology 11(3):139. https://doi.org/10.1088/0957-4484/11/3/301
Mirjavadi SS, Afshari BM, Barati MR, Hamouda AMS (2019) Transient response of porous FG nanoplates subjected to various pulse loads based on nonlocal stress-strain gradient theory. Eur J Mech A/Solids 74:210–220. https://doi.org/10.1016/j.euromechsol.2018.11.004
Mohamed N, Eltaher MA, Mohamed SA, Seddek LF (2019) Energy equivalent model in analysis of postbuckling of imperfect carbon nanotubes resting on nonlinear elastic foundation. Struct Eng Mech 70(6):737–750. https://doi.org/10.12989/sem.2019.70.6.737
Mohamed N, Mohamed SA, Eltaher MA (2020) Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Eng Comput. https://doi.org/10.1007/s00366-020-00976-2
Mohammadi M, Hosseini M, Shishesaz M, Hadi A, Rastgoo A (2019) Primary and secondary resonance analysis of porous functionally graded nanobeam resting on a nonlinear foundation subjected to mechanical and electrical loads. Eur J Mech A/Solids 77:103793. https://doi.org/10.1016/j.euromechsol.2019.05.008
Nix WD, Gao H (1998) Indentation size effects in crystalline materials: a law for strain gradient plasticity. J Mech Phys Solids 46(3):411–425. https://doi.org/10.1016/S0022-5096(97)00086-0
Park SK, Gao XL (2006) Bernoulli–Euler beam model based on a modified couple stress theory. J Micromech Microeng 16(11):2355. https://doi.org/10.1088/0960-1317/16/11/015
Pei YL, Geng PS, Li LX (2018) A modified higher-order theory for FG beams. Eur J Mech A/Solids 72:186–197. https://doi.org/10.1016/j.euromechsol.2018.05.008
Phung-Van P, Thai CH, Nguyen-Xuan H, Abdel-Wahab M (2019) An isogeometric approach of static and free vibration analyses for porous FG nanoplates. Eur J Mech A/Solids 78:103851. https://doi.org/10.1016/j.euromechsol.2019.103851
Pinnola FP, Faghidian SA, Barretta R, de Sciarra FM (2020) Variationally consistent dynamics of nonlocal gradient elastic beams. Int J Eng Sci 149:103220. https://doi.org/10.1016/j.ijengsci.2020.103220
Rabhi M, Benrahou KH, Kaci A, Houari MSA, Bourada F, Bousahla AA, Tounsi A (2020) A new innovative 3-unknowns HSDT for buckling and free vibration of exponentially graded sandwich plates resting on elastic foundations under various boundary conditions. Geomech Eng 22(2):119. https://doi.org/10.12989/gae.2020.22.2.119
Rapaport DC, Rapaport DCR (2004) The art of molecular dynamics simulation. Cambridge University Press, Cambridge
Rappé AK, Casewit CJ, Colwell KS, Goddard WA III, Skiff WM (1992) UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J Am Chem Soc 114(25):10024–10035. https://doi.org/10.1021/ja00051a040
Rebeiz GM (2004) RF MEMS: theory, design, and technology. John Wiley & Sons, New York
Reddy JN (2007) Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci 45(2–8):288–307. https://doi.org/10.1016/j.ijengsci.2007.04.004
Reddy JN (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48(11):1507–1518. https://doi.org/10.1016/j.ijengsci.2010.09.020
Sedighi HM (2014a) Size-dependent dynamic pull-in instability of vibrating electrically actuated microbeams based on the strain gradient elasticity theory. Acta Astronaut 95:111–123. https://doi.org/10.1016/j.actaastro.2013.10.020
Sedighi HM (2014b) The influence of small scale on the pull-in behavior of nonlocal nanobridges considering surface effect, Casimir and Van der Waals attractions. Int J Appl Mech 6(03):1450030. https://doi.org/10.1142/S1758825114500306
Shenoy VB (2005) Atomistic calculations of elastic properties of metallic fcc crystal surfaces. Phys Rev B 71(9):094104. https://doi.org/10.1103/PhysRevB.71.094104
She GL, Yuan FG, Karami B, Ren YR, Xiao WS (2019) On nonlinear bending behavior of FG porous curved nanotubes. Int J Eng Sci 135:58–74. https://doi.org/10.1016/j.ijengsci.2018.11.005
Sheng GG, Wang X (2018) Nonlinear vibration of FG beams subjected to parametric and external excitations. Eur J Mech A/Solids 71:224–234. https://doi.org/10.1016/j.euromechsol.2018.04.003
Shodja HM, Delfani MR (2011) A novel nonlinear constitutive relation for graphene and its consequence for developing closed-form expressions for Young’s modulus and critical buckling strain of single-walled carbon nanotubes. Acta Mech 222(1–2):91. https://doi.org/10.1007/s00707-011-0528-5
Shokrieh MM, Rafiee R (2010) Prediction of Young’s modulus of graphene sheets and carbon nanotubes using nanoscale continuum mechanics approach. Mater Des 31(2):790–795. https://doi.org/10.1016/j.matdes.2009.07.058
Şimşek M, Kocatürk T, Akbaş ŞD (2013) Static bending of a functionally graded microscale Timoshenko beam based on the modified couple stress theory. Compos Struct 95:740–747. https://doi.org/10.1016/j.compstruct.2012.08.036
Şimşek M, Yurtcu HH (2013) Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos Struct 97:378–386. https://doi.org/10.1016/j.compstruct.2012.10.038
Thai HT, Vo TP, Nguyen TK, Lee J (2015) Size-dependent behavior of functionally graded sandwich microbeams based on the modified couple stress theory. Compos Struct 123:337–349. https://doi.org/10.1016/j.compstruct.2014.11.065
Thai S, Thai HT, Vo TP, Patel VI (2018) A simple shear deformation theory for nonlocal beams. Compos Struct 183:262–270. https://doi.org/10.1016/j.compstruct.2017.03.022
Toupin RA (1964) Theories of elasticity with couple-stress. Arch Ration Mech Anal 17:85–112. https://doi.org/10.1007/BF00253050
Wang GF, Feng XQ (2007) Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Appl Phys Lett 90(23):231904. https://doi.org/10.1063/1.2746950
Wu Y, Zhang X, Leung AYT, Zhong W (2006) An energy-equivalent model on studying the mechanical properties of single-walled carbon nanotubes. Thin-walled Struct 44(6):667–676. https://doi.org/10.1016/j.tws.2006.05.003
Yang FACM, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743. https://doi.org/10.1016/S0020-7683(02)00152-X
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Abdelrahman, A.A., Eltaher, M.A. On bending and buckling responses of perforated nanobeams including surface energy for different beams theories. Engineering with Computers 38, 2385–2411 (2022). https://doi.org/10.1007/s00366-020-01211-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-020-01211-8