Skip to main content
Springer Nature Link
Log in

A numerical method for fractional variable order pantograph differential equations based on Haar wavelet

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

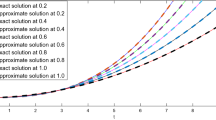
In this article, Haar wavelet collocation technique is developed for the solution of variable order fractional pantograph differential equations. The Haar technique reduces the given equations into a system of linear algebraic equations. The derived system is then solved by Gaussian elimination method. Through fixed point theory, we develop some requisite conditions for the existence of at most one solution of the underlying problem endowed with initial conditions. Some numerical examples are also given for checking the validation and convergence of the concerned method. The mean square root and maximum absolute errors for different number of collocation points have been calculated. The results indicate that Haar method is efficient for solving such equations. Fractional derivative is described in the Caputo sense.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Kilbas AA, Marichev OI, Samko SG (1993) Fractional integrals and derivatives (theory and applications). Gordon and Breach, Lausanne

    MATH  Google Scholar 

  2. Zhang L, Hou W (2020) Standing waves of nonlinear fractional p-Laplacian Schrödinger equation involving logarithmic nonlinearity. Appl Math Lett. https://doi.org/10.1016/j.aml.2019.106149

    Article  MATH  Google Scholar 

  3. Wang G, Pei K, Chen Y (2019) Stability analysis of nonlinear Hadamard fractional differential system. J Frankl Inst 356:6538–6546

    Article  MathSciNet  Google Scholar 

  4. Valério D, Da Costa JS (2011) Variable-order fractional derivatives and their numerical approximations. Signal Process 91(3):470–483

    Article  Google Scholar 

  5. Macdonald AS, Baxter A, Lamberton B (1997) Financial calculus; stochastic calculus applied to finance. Br Actuar J 3(2):485

    Article  Google Scholar 

  6. Ghanbari B, Atangana A (2020) Some new edge detecting techniques based on fractional derivatives with non-local and non-singular kernels. Adv Differ Equ 2020(1):1–19

    Article  MathSciNet  Google Scholar 

  7. Li D, Zhang C (2020) Long time numerical behaviors of fractional pantograph equations. Math Comput Simul 172:244–257

    Article  MathSciNet  Google Scholar 

  8. Wang G, Pei K, Agarwal R et al (2018) Nonlocal Hadamard fractional boundary value problem with Hadamard integral and discrete boundary conditions on a half-line. J Comput Appl Math 343:230–239

    Article  MathSciNet  Google Scholar 

  9. Sedaghat S, Ordokhani Y, Dehghan M (2012) Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun Nonlinear Sci Numer Simul 17(12):4815–4830

    Article  MathSciNet  Google Scholar 

  10. Bahsi M, Cevik M, Sezer M (2015) Orthoexponential polynomial solutions of delay pantograph differential equations with residual error estimation. Appl Math Comput 271:11–21

    MathSciNet  MATH  Google Scholar 

  11. Atangana A (2017) Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fract 102:396–406

    Article  MathSciNet  Google Scholar 

  12. Rossetti M, Bardella P, Montrosset I (2011) Modeling passive mode-locking in quantum dot lasers: a comparison between a finite-difference traveling-wave model and a delayed differential equation approach. IEEE J Quantum Electron 47(5):569–576

    Article  Google Scholar 

  13. Hale JK, Lunel SM (2013) Introduction to functional differential equations. Springer Science & Business Media, New York

    MATH  Google Scholar 

  14. Ali I, Brunner H, Tang T (2009) A spectral method for pantograph-type delay differential equations and its convergence analysis. J Comput Math 27(2/3):254–265

    MathSciNet  MATH  Google Scholar 

  15. Ali A, Shah K, Abdeljawad T (2020) Study of implicit delay fractional differential equations under anti-periodic boundary conditions. Adv Differ Equ 2020(1):1–16

    Article  MathSciNet  Google Scholar 

  16. Iqbal M, Shah K, Khan RA (2019) On using coupled fixed point theorems for mild solutions to coupled system of multi-point boundary value problems of nonlinear fractional hybrid pantograph differential equations. Math Methods Appl Sci 44:1–14

    Google Scholar 

  17. Avazzadeh Z, Heydari MH, Mahmoudi MR (2020) An approximate approach for the generalized variable-order fractional pantograph equation. Alex Eng J 59(4):2347–2354

    Article  Google Scholar 

  18. Samko SG (2013) Fractional integration and differentiation of variable order: an overview. Nonlinear Dyn 71:653–662

    Article  MathSciNet  Google Scholar 

  19. Sun HG, Chen W, Wei H, Chen YQ (2011) A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur Phys J Spec Top 193:185–192

    Article  Google Scholar 

  20. Li M (2010) Fractal time series—a tutorial review. Math Probl Eng. https://doi.org/10.1155/2010/157264

  21. Lin R, Liu F, Anh V, Turner I (2009) Stability and convergence of a new explicit finite-difference approximation for the variable order nonlinear fractional diffusion equation. Appl Math Comput 212(2):435–445

    MathSciNet  MATH  Google Scholar 

  22. Roohi R, Heydari MH, Bavi O, Emdad H (2019) Chebyshev polynomials for generalized Couette flow of fractional Jeffrey nanofluid subjected to several thermochemical effects. Eng Comput 2019:1–17

    Google Scholar 

  23. Hosseininia M, Heydari MH, Rouzegar J, Cattani C (2019) A meshless method to solve nonlinear variable-order time fractional 2D reaction diffusion equation involving Mittag-Leffler kernel. Eng Comput 2019:1–13

    Google Scholar 

  24. Hossininia M, Heydari MH (2019) Legendre wavelets for the numerical solution of nonlinear variable-order time fractional 2D reaction–diffusion equation involving Mittag–Leffler nonsingular kernel. Chaos Solitons Frac 127:400–407

    Article  Google Scholar 

  25. Sun H, Chang A, Zhang Y, Chen W (2019) A review on variable-order fractional differential equations: mathematical foundations, physical models, numerical methods and applications. Fract Calc Appl Anal 22(1):27–59

    Article  MathSciNet  Google Scholar 

  26. Yang X, Machado JAT (2017) A new fractional operator of variable order: application in the description of anomalous diffusion. Phys A 481:276–283

    Article  MathSciNet  Google Scholar 

  27. Sun H et al (2019) A review on variable-order fractional differential equations: mathematical foundations, physical models, numerical methods and applications. Fract Calc Appl Anal 22(1):27–59

    Article  MathSciNet  Google Scholar 

  28. Xu Y, He Z (2013) Existence and uniqueness results for Cauchy problem of variable-order fractional differential equations. J Appl Math Comput 43(1–2):295–306

    Article  MathSciNet  Google Scholar 

  29. Razminia A, Dizaji AF, Majd VJ (2012) Solution existence for non-autonomous variable-order fractional differential equations. Math Comput Modell 55(3–4):1106–1117

    Article  MathSciNet  Google Scholar 

  30. Hartley T, Lorenzo CF (2002) Dynamics and control of initialized fractional-order systems. Nonlinear Dyn 29:201–233

    Article  MathSciNet  Google Scholar 

  31. Babolian E, Shahsavaran A (2009) Numerical solution of nonlinear Fredholm integral equations of the second kind using Haar wavelets. J Comput Appl Math 225:87–95

    Article  MathSciNet  Google Scholar 

  32. Chen C, Hsiao C (1997) Haar wavelet method for solving lumped and distributed-parameter systems. IEE Proc Control Theory Appl 144:87–94

    Article  Google Scholar 

  33. Lepik U, Tamme E (2007) Solution of nonlinear Fredholm integral equations via the Haar wavelet method. Proc Estonian Acad Sci Phys Mat. 56(1):17–27

    Article  MathSciNet  Google Scholar 

  34. Li Y, Zhao W (2010) Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl Math Comput 216:2276–2285

    MathSciNet  MATH  Google Scholar 

  35. Lepik U (2009) Solving fractional integral equations by the Haar wavelet method. Appl Math Comput 214(2):468–478

    MathSciNet  MATH  Google Scholar 

  36. Heydari M, Loghmani GB, Hosseini SM (2013) Operational matrices of Chebyshev cardinal functions and their application for solving delay differential equations arising in electrodynamics with error estimation. Appl Math Model 37:7789–7809

    Article  MathSciNet  Google Scholar 

  37. Rahimkhani P, Ordokhani Y, Babolian E (2017) Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. J Comput Appl Math 309:493–510

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We are thankful to the reviewers for their careful reading and suggestions.

Funding

There is no source to support this article financially.

Author information

Authors and Affiliations

  1. College of Engineering, Al Ain University, Al Ain, United Arab Emirates

    Hussam Alrabaiah

  2. Department of Mathematics, Tafila Technical University, Tafila, Jordan

    Hussam Alrabaiah

  3. Department of Mathematics, University of Malakand, Chakdara Dir (Lower), Khyber Pakhtunkhawa, Pakistan

    Israr Ahmad & Kamal Shah

  4. Department of Mathematics, University of Peshawar, Peshawar, Khyber Pakhtunkhwa, Pakistan

    Rohul Amin

Authors
  1. Hussam Alrabaiah
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Israr Ahmad
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rohul Amin
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Kamal Shah
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hussam Alrabaiah.

Ethics declarations

Conflict of interest

There exist no conflict of interest regarding this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alrabaiah, H., Ahmad, I., Amin, R. et al. A numerical method for fractional variable order pantograph differential equations based on Haar wavelet. Engineering with Computers 38, 2655–2668 (2022). https://doi.org/10.1007/s00366-020-01227-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01227-0

Keywords