A third order shear deformable model and its applications for nonlinear dynamic response of graphene oxides reinforced curved beams resting on visco-elastic foundation and subjected to moving loads

Abstract

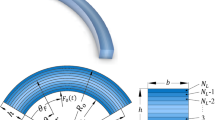
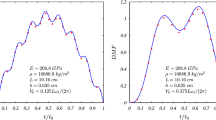
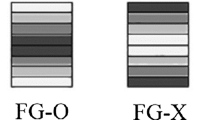
In present work, a nonlinear functionally graded curved beam model including the von Kármán geometric nonlinearity is developed on the basis of the third-order shear deformation theory. Due to incorporating the trapezoidal shape factor in the proposed model, the errors caused by geometric curvatures are eliminated. The governing equations of motions related to the dynamics of curved beams are derived by Lagrange method and solved using a standard Newmark time iteration procedure in conjunction with Newton–Raphson technique. Some comparisons are performed and indicate that the results from our model coincide favorably with semi-analytical solutions. Afterwards, utilizing the proposed model, the present investigation focuses on the nonlinear transient response of functionally graded multilayer curved beams reinforced by graphene oxide nano-fillers subjected to moving loads. A modified Halpin–Tsai micromechanical model is implemented to determine the effective modulus of graphene oxide/polymer nanocomposite, and the rule of mixture is used to calculate the mass density and Poisson’s ratio. The curved beams are assumed to rest on a visco-Pasternak foundation. The effects GO nano-fillers, including their weight fractions, distribution patterns and size on the nonlinear dynamic responses of the nanocomposite curved beams subjected to moving loads are studied. Moreover, the effects of radius-to-span ratios and visco-Pasternak foundation on the nonlinear dynamic response of curved beams are also discussed as subtopics.

Appendix

The details of the matrix in governing equations Eq. (28) are given in the following:

$$\left[ {\mathbf{K}} \right]_{{\text{L}}} = \left[ {\begin{array}{*{20}c} {K_{{\text{L}}}^{11} } & {K_{{\text{L}}}^{12} } & {K_{{\text{L}}}^{13} } \\ {\left( {K_{{\text{L}}}^{12} } \right)^{{\text{T}}} } & {K_{{\text{L}}}^{22} } & {K_{{\text{L}}}^{23} } \\ {\left( {K_{{\text{L}}}^{13} } \right)^{{\text{T}}} } & {\left( {K_{{\text{L}}}^{23} } \right)^{{\text{T}}} } & {K_{{\text{L}}}^{33} } \\ \end{array} } \right]$$

(31)

in which

$$K_{{\text{L}}}^{11} = \int\limits_{0}^{\vartheta } {\left( {L_{10} \frac{{\partial {{\varvec{\upalpha}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upalpha}}}^{{\text{T}}} }}{\partial \theta }} \right){\text{d}}\theta } ;\quad K_{{\text{L}}}^{12} = \int\limits_{0}^{\vartheta } {\left( {L_{14} \frac{{\partial {{\varvec{\upalpha}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upbeta}}}^{{\text{T}}} }}{\partial \theta }} \right){\text{d}}\theta } ;\quad K_{{\text{L}}}^{13} = \int\limits_{0}^{\vartheta } {\left( {L_{15} \frac{{\partial {{\varvec{\upalpha}}}}}{\partial \theta }\frac{{\partial^{2} {{\varvec{\upxi}}}^{{\text{T}}} }}{{\partial^{2} \theta }} + L_{16} \frac{{\partial {{\varvec{\upalpha}}}}}{\partial \theta }{{\varvec{\upxi}}}^{{\text{T}}} } \right){\text{d}}\theta } ;$$

$$K_{{\text{L}}}^{22} = \int\limits_{0}^{\vartheta } {\left( {L_{11} \frac{{\partial {{\varvec{\upbeta}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upbeta}}}^{{\text{T}}} }}{\partial \theta } + L_{55} {\mathbf{\beta \beta }}^{{\text{T}}} } \right){\text{d}}\theta } ;\quad K_{{\text{L}}}^{23} = \int\limits_{0}^{\vartheta } {\left( {L_{17} \frac{{\partial {{\varvec{\upbeta}}}}}{\partial \theta }\frac{{\partial^{2} {{\varvec{\upxi}}}^{{\text{T}}} }}{{\partial^{2} \theta }} + L_{18} \frac{{\partial {{\varvec{\upbeta}}}}}{\partial \theta }{{\varvec{\upxi}}}^{{\text{T}}} } \right){\text{d}}\theta } ;\quad$$

$$K_{{\text{L}}}^{33} = \int\limits_{0}^{\vartheta } {\left( {L_{12} \frac{{\partial^{2} {{\varvec{\upxi}}}}}{{\partial^{2} \theta }}\frac{{\partial^{2} {{\varvec{\upxi}}}^{{\text{T}}} }}{{\partial^{2} \theta }} + 2L_{19} \frac{{\partial^{2} {{\varvec{\upxi}}}}}{{\partial^{2} \theta }}{{\varvec{\upxi}}}^{{\text{T}}} + L_{13} {\mathbf{\xi \xi }}^{{\text{T}}} } \right){\text{d}}\theta }$$

$$\left[ {\mathbf{K}} \right]_{{{\text{NL}}}} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {0_{m \times m} } & {0_{m \times m} } & {K_{{{\text{NL}}}}^{13} } \\ {0_{m \times m} } & {0_{m \times m} } & {K_{{{\text{NL}}}}^{23} } \\ {\left( {K_{{{\text{NL}}}}^{13} } \right)^{{\text{T}}} } & {\left( {K_{{{\text{NL}}}}^{23} } \right)^{{\text{T}}} } & {K_{{{\text{NL}}}}^{33} } \\ \end{array} } \right]$$

(32)

in which

$$K_{{{\text{NL}}}}^{13} = \int\limits_{0}^{\vartheta } {\left[ {N_{11} \left( {\frac{\partial w}{{\partial \theta }}} \right)\left( {\frac{{\partial {{\varvec{\upalpha}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta }} \right)} \right]{\text{d}}\theta } ;\quad K_{{{\text{NL}}}}^{23} = \int\limits_{0}^{\vartheta } {\left[ {N_{12} \left( {\frac{\partial w}{{\partial \theta }}} \right)\left( {\frac{{\partial {{\varvec{\upbeta}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta }} \right)} \right]{\text{d}}\theta } ;$$

$$K_{{{\text{NL}}}}^{33} = \int\limits_{0}^{\vartheta } {\left[ {\left( {N_{11} \frac{{\partial v_{0} }}{\partial \theta } + N_{12} \frac{{\partial v_{1} }}{\partial \theta } - 2N_{13} \frac{{\partial^{2} w}}{{\partial \theta^{2} }} + 2N_{14} w + N_{15} \left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} } \right)\frac{{\partial {{\varvec{\upxi}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta } - N_{13} \frac{\partial w}{{\partial \theta }}\frac{{\partial^{2} {{\varvec{\upxi}}}}}{{\partial \theta^{2} }}\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta } + N_{14} \frac{\partial w}{{\partial \theta }}{{\varvec{\upxi}}}\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta }} \right]{\text{d}}\theta }$$

$$\left[ {\mathbf{M}} \right] = \left[ {\begin{array}{*{20}c} {M_{{}}^{11} } & {M_{{}}^{12} } & {M_{{}}^{13} } \\ {\left( {M_{{}}^{12} } \right)^{{\text{T}}} } & {M_{{}}^{22} } & {M_{{}}^{23} } \\ {\left( {M_{{}}^{13} } \right)^{{\text{T}}} } & {\left( {M_{{}}^{23} } \right)^{{\text{T}}} } & {M_{{}}^{33} } \\ \end{array} } \right]$$

(33)

in which

$$M_{{}}^{11} = \int\limits_{0}^{\vartheta } {\left( {I_{0} {\mathbf{\alpha \alpha }}^{{\text{T}}} } \right){\text{d}}\theta } ;\quad M_{{}}^{12} = \int\limits_{0}^{\vartheta } {\left( {I_{f} {\mathbf{\alpha \beta }}^{{\text{T}}} } \right){\text{d}}\theta } ;\quad M_{{}}^{13} = -\int\limits_{0}^{\vartheta } {\left( {I_{1} {{\varvec{\upalpha}}}\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta }} \right){\text{d}}\theta } ;$$

$$M_{{}}^{22} = \int\limits_{0}^{\vartheta } {\left( {I_{ff} {\mathbf{\beta \beta }}^{{\text{T}}} } \right){\text{d}}\theta } ;\quad M_{{}}^{23} = - \int\limits_{0}^{\vartheta } {\left( {I_{zf} {{\varvec{\upbeta}}}\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta }} \right){\text{d}}\theta } ;$$

$$M_{{}}^{33} = \int\limits_{0}^{\vartheta } {\left( {I_{2} \frac{{\partial {{\varvec{\upxi}}}}}{\partial \theta }\frac{{\partial {{\varvec{\upxi}}}^{{\text{T}}} }}{\partial \theta } + I_{{\text{R}}} {\mathbf{\xi \xi }}^{{\text{T}}} } \right){\text{d}}\theta }$$