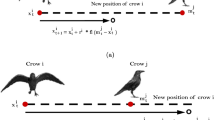
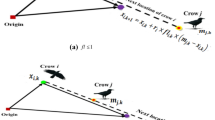
Abstract
Due to the use of space structures in monumental and significant buildings, providing adequate safety and proper structural performance must always be taken into account. In this study, the geometric and material nonlinear behaviors are directly considered in the design of space structures so that the resulting designs are economical while having appropriate collapse behavior. Weight and collapse energy are considered the objective functions, and the problem is considered as a multi-objective optimization problem. This is the first attempt to combine the weight and collapse energy simultaneously for the optimal design of structures. To solve such problems, two new multi-objective algorithms based on the recently introduced crow search algorithm (CSA) have been proposed. These algorithms are called multi-objective crow search algorithm (MOCSA) and multi-objective modified crow search algorithm (MOMCSA). MOCSA and MOMCSA have similar structures and details, except that the MOCSA generates the new solution as the CSA approach does while generating the new solution in the MOMCSA is modified. The modification of the search vector and the search range is employed as two simple and effective changes in MOMCSA to enhance the exploration and exploitation. To evaluate the proposed algorithms, three space structures were optimized using the proposed algorithms and two well-known algorithms, MOPSO and NSGA-II. The results indicate superiority of MOMCSA to the other algorithms.














Similar content being viewed by others
References
Schmidt LC, Morgan P, Hanaor A (1982) Ultimate load testing of space trusses. J Struct Div 108(6):1324–1335
Hanaor A, Marsh C, Parke GA (1989) Modification of behavior of double-layer grids: overview. J Struct Eng 115(5):1021–1037
Sheidaii MR, Parke GAR, Abedi K, Behravesh A (2001) Dynamic snap-through buckling of truss-type structures. Int J Space Struct 16(2):85–93
Rashidyan S, Sheidaii MR (2017) Improving double-layer space trusses collapse behavior by strengthening compression layer and weakening tension layer members. Adv Struct Eng 20(11):1757–1767
Gholizadeh S, Baghchevan A (2017) Multi-objective seismic design optimization of steel frames by a chaotic meta-heuristic algorithm. Eng Comput 33(4):1045–1060
Deb K (2001) Multi objective optimization using evolutionary algorithms. Wiley, Chichester
Zavala GR, Nebro AJ, Luna F, Coello Coello CA (2013) A survey of multi-objective metaheuristics applied to structural optimization. Struct Multidiscip Optim 49(4):537–558
Papadrakakis M, Lagaros ND, Plevris V (2002) Multi-objective Optimization of skeletal structures under static and seismic loading conditions. Eng Optim 34:645–669
Luh GC, Chueh CH (2004) Multi-objective optimal design of truss structure with immune algorithm. Comput Struct 82(11–12):829–844
Coello CA, Toscano G (2005) Multiobjective structural optimization using a micro-genetic algorithm. Struct Multidiscip Optim 30(5):388–403
Paya I, Yepes V, Gonz´alez-Vidosa F, Hospitaler A (2008) Multiobjective optimization of concrete frames by simulated annealing. Comput-Aided Civ Inf 23(8):596–610
Su R, Wang X, Gui L, Fan Z (2011) Multi-objective topology and sizing optimization of truss structures based on adaptive multi-island search strategy. Struct Multidiscip Optim 43(2):275–286
Kaveh A, Laknejadi K (2013) A new multi-swarm multi-objective optimization method for structural design. Adv Eng Softw 58:54–69
Xiong Z, Li XH, Liang JC, Li LJ (2018) A multi-objective hybrid algorithm for optimization of grid structures. Int J Appl Mech 10(01):1850009
Kaveh A, Mahdavi VR (2019) Multi-objective colliding bodies optimization algorithm for design of trusses. J Comput Des Eng 6(1):49–59
Gholizadeh S, Fattahi F (2019) Multi-objective design optimization of steel moment frames considering seismic collapse safety. Eng Comput pp.1–14. https://doi.org/10.1007/s00366-019-00886-y
Tejani GG, Pholdee N, Bureerat S, Prayogo D, Gandomi AH (2019) Structural optimization using multi-objective modified adaptive symbiotic organisms search. Expert Syst Appl 125:425–441
Techasen T, Wansasueb K, Panagant N, Pholdee N, Bureerat S (2019) Simultaneous topology, shape, and size optimization of trusses, taking account of uncertainties using multi-objective evolutionary algorithms. Eng Comput 35(2):721–740
Kumar S, Tejani GG, Pholdee N, Bureerat S (2020) Multi-objective modified heat transfer search for truss optimization. Eng Comput pp.1–16. https://doi.org/10.1007/s00366-020-01010-1
Askarzadeh A (2016) A novel metaheuristic method for solving constrained engineering optimization problems: crow search algorithm. Comput Struct 169:1–12
Jain M, Rani A, Singh V (2017) An improved crow search algorithm for high-dimensional problems. J Intell Fuzzy Syst 33(6):3597–3614
Allaoui M, Ahiod B, El-Yafrani M (2018) A hybrid crow search algorithm for solving the DNA fragment assembly problem. Expert Syst Appl 102:44–56
Movahediyan Z, Askarzadeh A (2018) Multi-objective optimization framework of a photovoltaic-diesel generator hybrid energy system considering operating reserve. Sustain Cities Soc 41:1–12
Hinojosa S, Oliva D, Cuevas E, Pajares G, Avalos O, Gálvez J (2018) Improving multi-criterion optimization with chaos: a novel multi-objective chaotic crow search algorithm. Neural Comput Appl 29(8):319–335
Fallah H, Kisi O, Kim S, Rezaie-Balf M (2019) A new optimization approach for the least-cost design of water distribution networks: improved crow search algorithm. Water Resour Manag 33(10):3595–3613
Rizk-Allah RM, Hassanien AE, Slowik A (2020) Multi-objective orthogonal opposition-based crow search algorithm for large-scale multi-objective optimization. Neural Comput Appl 32(17):1–32
Makhdoomi S, Askarzadeh A (2020) Optimizing operation of a photovoltaic/diesel generator hybrid energy system with pumped hydro storage by a modified crow search algorithm. J Energy Storage 27:101040
Javidi A, Salajegheh E, Salajegheh J (2019) Enhanced crow search algorithm for optimum design of structures. Appl Soft Comput 77:274–289
Coello CAC, Pulido GT, Lechuga MS (2004) Handling multiple objectives with particle swarm optimization. IEEE Trans Evol Comput 8(3):256–279
Deb K, Pratap A, Agarwal S, Meyarivan TA (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Coello CAC, Van Veldhuizen DA, Lamont GB (2002) Evolutionary algorithms for solving multi-objective problems. Kluwer Academic Publishers, New York
McKenna F, Fenves GL (2001) The OpenSees command language manual. Pacific Earthquake Engineering Research Center, University of California, Berkeley
Kamyab R, Salajegheh E (2013) Size optimization of nonlinear scallop domes by an enhanced particle swarm algorithm. Int J Civ Eng 11(3):77–89
Hassanzadeh A, Gholizadeh S (2019) Collapse-performance-aided design optimization of steel concentrically braced frames. Eng Struct 197:109411
Gholizadeh S, Moghadas RK (2014) Performance-based optimum design of steel frames by an improved quantum particle swarm optimization. Adv Struct Eng 17(2):143–156
Gholizadeh S, Ebadijalal M (2018) Performance based discrete topology optimization of steel braced frames by a new metaheuristic. Adv Eng Softw 123:77–92
Rezazadeh F, Talatahari S (2020) Seismic energy-based design of BRB frames using multi-objective vibrating particles system optimization. Structures 24:227–239
Hill CD, Blandford GE, Wang ST (1989) Post-buckling analysis of steel space trusses. J Struct Eng ASCE 115(4):900–919
Ramesh G, Krishnamoorthy CS (1994) Inelastic post-buckling analysis of truss structures by dynamic relaxation method. Int J Numer Methods Eng 37(21):3633–3657
Thai HT, Kim SE (2009) Large deflection inelastic analysis of space trusses using generalized displacement control method. J Constr Steel Res 65(10–11):1987–1994
Thai HT, Kim SE (2011) Nonlinear inelastic time-history analysis of truss structures. J Constr Steel Res 67(12):1966–1972
Thai HT, Kim SE (2011) Practical advanced analysis software for nonlinear inelastic dynamic analysis of steel structures. J Constr Steel Res 67(3):453–461
Truong VH, Kim SE (2018) Reliability-based design optimization of nonlinear inelastic trusses using improved differential evolution algorithm. Adv Eng Softw 121:59–74
Knowles JD, Corne DW (2000) Approximating the nondominated front using the Pareto archived evolution strategy. Evol Comput 8(2):149–172
Yang XS, Deb S, Fong S (2014) Metaheuristic algorithms: optimal balance of intensification and diversification. Appl Math Inf Sci 8(3):977
Zitzler E, Deb K, Thiele L (2000) Comparison of multi-objective evolutionaryalgorithms:empirical results. Evol Comput 8(2):173–195
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Javidi, A., Salajegheh, E. & Salajegheh, J. Optimization of weight and collapse energy of space structures using the multi-objective modified crow search algorithm. Engineering with Computers 38, 2879–2896 (2022). https://doi.org/10.1007/s00366-020-01276-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-020-01276-5