Skip to main content

Advertisement

Springer Nature Link
Log in

Novel hybrid machine leaning model for predicting shear strength of reinforced concrete shear walls

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

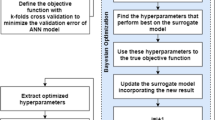
Accurate prediction of the ultimate shear capacity of reinforced concrete shear walls (RCSWs) is essential for robust design of buildings under seismic and wind loads. However, the shear capacity of RCSWs depends on multiple complex design variables characterized by diverse geometric and materials properties. Thus, a powerful modeling framework is required. In this paper, a hybrid artificial intelligence model is proposed for predicting the ultimate shear capacity of RCSWs named artificial neural network (ANN) coupled with adaptive harmony search optimization (AHS) algorithm. Different statistical metrics were used to compare the performances of the ANN model coupled with AHS (ANN-AHS) to three existing empirical relations and two ANN models combined with harmony search (ANN-HS) and global-best harmony search (ANN-GHS). Results show that the proposed ANN-AHS achieved superior performance in modelling the shear strength of RCSWs compared to ANN-HS and ANN-GHS models. The soft-computing models have proven to be more accurate than existing empirical relations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Fintel M (1991) Shearwalls—an answer for seismic resistance? Concr Int 13(7):48–53

    Google Scholar 

  2. Darwin D, Dolan CW, Nilson AH (2016) Design of concrete structures. McGraw-Hill Education, New York

    Google Scholar 

  3. ACI Committee 318 (2019)Committee A Building code requirements for structural concrete (318M-19) and commentary

  4. Code P (2005) Eurocode 8: Design of structures for earthquake resistance-part 1: general rules, seismic actions and rules for buildings. European Committee for Standardization, Brussels

    Google Scholar 

  5. Teng S, Chandra J (2016) Cyclic shear behavior of high strength concrete structural walls. Petra Christian University, Surabaya

    Book  Google Scholar 

  6. Chandra J, Chanthabouala K, Teng S (2018) Truss model for shear strength of structural concrete walls. ACI Struct J 115(2):323–335

    Article  Google Scholar 

  7. Lu Y, Henry RS (2017) Numerical modelling of reinforced concrete walls with minimum vertical reinforcement. Eng Struct 143:330–345. https://doi.org/10.1016/j.engstruct.2017.02.043

    Article  Google Scholar 

  8. Mazars J, Kotronis P, Davenne L (2002) A new modelling strategy for the behaviour of shear walls under dynamic loading. Earthq Eng Struct Dyn 31(4):937–954. https://doi.org/10.1002/eqe.131

    Article  Google Scholar 

  9. Farvashany FE (2017) Parametric studies on reinforced concrete shear walls: an engineering response to Einstein’s riddle? ACI Struct J 114(5):1099–1108

    Article  Google Scholar 

  10. Baghi H, Baghi H, Siavashi S (2019) Novel empirical expression to predict shear strength of reinforced concrete walls based on particle swarm optimization. ACI Struct J 116(5):247–260

    Article  Google Scholar 

  11. Shahriar A, Nehdi M (2013) Modeling rheological properties of oil well cement slurries using multiple regression analysis and artificial neural networks. Int J Mater Sci 3(1):26–37

    Google Scholar 

  12. Abuodeh OR, Abdalla JA, Hawileh RA (2020) Assessment of compressive strength of ultra-high performance concrete using deep machine learning techniques. Appl Soft Comput 95:106552. https://doi.org/10.1016/j.asoc.2020.106552

    Article  Google Scholar 

  13. Ghaleini EN, Koopialipoor M, Momenzadeh M, Sarafraz ME, Mohamad ET, Gordan B (2019) A combination of artificial bee colony and neural network for approximating the safety factor of retaining walls. Eng Comput 35(2):647–658. https://doi.org/10.1007/s00366-018-0625-3

    Article  Google Scholar 

  14. Al-Musawi AA, Alwanas AAH, Salih SQ, Ali ZH, Tran MT, Yaseen ZM (2020) Shear strength of SFRCB without stirrups simulation: implementation of hybrid artificial intelligence model. Eng Comput 36(1):1–11. https://doi.org/10.1007/s00366-018-0681-8

    Article  Google Scholar 

  15. Zhang G, Ali ZH, Aldlemy MS, Mussa MH, Salih SQ, Hameed MM, Al-Khafaji ZS, Yaseen ZM (2020) Reinforced concrete deep beam shear strength capacity modelling using an integrative bio-inspired algorithm with an artificial intelligence model. Eng Comput. https://doi.org/10.1007/s00366-020-01137-1

    Article  Google Scholar 

  16. Gaspar B, Teixeira A, Soares CG (2017) Adaptive surrogate model with active refinement combining Kriging and a trust region method. Reliab Eng Syst Saf 165:277–291

    Article  Google Scholar 

  17. Xiao M, Zhang J, Gao L (2020) A system active learning Kriging method for system reliability-based design optimization with a multiple response model. Reliab Eng Syst Saf 199:106935. https://doi.org/10.1016/j.ress.2020.106935

    Article  Google Scholar 

  18. Xiao M, Zhang J, Gao L, Lee S, Eshghi AT (2019) An efficient Kriging-based subset simulation method for hybrid reliability analysis under random and interval variables with small failure probability. Struct Multidiscip Optim 59(6):2077–2092

    Article  MathSciNet  Google Scholar 

  19. Zhang J, Gao L, Xiao M (2020) A new hybrid reliability-based design optimization method under random and interval uncertainties. Int J Numer Methods Eng. https://doi.org/10.1002/nme.6440

    Article  MathSciNet  Google Scholar 

  20. Zhang J, Xiao M, Gao L, Chu S (2019) A combined projection-outline-based active learning Kriging and adaptive importance sampling method for hybrid reliability analysis with small failure probabilities. Comput Methods Appl Mech Eng 344:13–33

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhang J, Xiao M, Gao L, Fu J (2018) A novel projection outline based active learning method and its combination with Kriging metamodel for hybrid reliability analysis with random and interval variables. Comput Methods Appl Mech Eng 341:32–52

    Article  MathSciNet  MATH  Google Scholar 

  22. Chojaczyk A, Teixeira A, Neves LC, Cardoso J, Soares CG (2015) Review and application of artificial neural networks models in reliability analysis of steel structures. Struct Saf 52:78–89

    Article  Google Scholar 

  23. Dai H, Zhang H, Wang W (2012) A support vector density-based importance sampling for reliability assessment. Reliab Eng Syst Saf 106:86–93

    Article  Google Scholar 

  24. Xiao M, Gao L, Xiong H, Luo Z (2015) An efficient method for reliability analysis under epistemic uncertainty based on evidence theory and support vector regression. J Eng Des 26(10–12):340–364

    Article  Google Scholar 

  25. Zhang J, Xiao M, Gao L, Chu S (2019) Probability and interval hybrid reliability analysis based on adaptive local approximation of projection outlines using support vector machine. Comput Aided Civ Infrastruct Eng 34(11):991–1009

    Article  Google Scholar 

  26. Fei C-W, Li H, Liu H-T, Lu C, An L-Q, Han L, Zhao Y-J (2020) Enhanced network learning model with intelligent operator for the motion reliability evaluation of flexible mechanism. Aerosp Sci Technol 107:106342. https://doi.org/10.1016/j.ast.2020.106342

    Article  Google Scholar 

  27. Keshtegar B, Meng D, Ben Seghier MEA, Xiao M, Trung N-T, Bui DT (2020) A hybrid sufficient performance measure approach to improve robustness and efficiency of reliability-based design optimization. Eng Comput. https://doi.org/10.1007/s00366-019-00907-w

    Article  Google Scholar 

  28. Keshtegar B, Kisi O (2017) M5 model tree and Monte Carlo simulation for efficient structural reliability analysis. Appl Math Model 48:899–910

    Article  MathSciNet  MATH  Google Scholar 

  29. Keshtegar B, Bagheri M, Fei C-W, Lu C, Taylan O, Thai D-K (2021) Multi-extremum-modified response basis model for nonlinear response prediction of dynamic turbine blisk. Eng Comput. https://doi.org/10.1007/s00366-020-01273-8

    Article  Google Scholar 

  30. Jiang C, Qiu H, Li X, Chen Z, Gao L, Li P (2020) Iterative reliable design space approach for efficient reliability-based design optimization. Eng Comput 36(1):151–169. https://doi.org/10.1007/s00366-018-00691-z

    Article  Google Scholar 

  31. Gao L, Xiao M, Shao X, Jiang P, Nie L, Qiu H (2012) Analysis of gene expression programming for approximation in engineering design. Struct Multidiscip Optim 46(3):399–413. https://doi.org/10.1007/s00158-012-0767-7

    Article  Google Scholar 

  32. Zhu S-P, Keshtegar B, Chakraborty S, Trung N-T (2020) Novel probabilistic model for searching most probable point in structural reliability analysis. Comput Methods Appl Mech Eng 366:113027. https://doi.org/10.1016/j.cma.2020.113027

    Article  MathSciNet  MATH  Google Scholar 

  33. Zhang Y, Gao L, Xiao M (2020) Maximizing natural frequencies of inhomogeneous cellular structures by Kriging-assisted multiscale topology optimization. Comput Struct 230:106197

    Article  Google Scholar 

  34. Fei C-W, Lu C, Liem RP (2019) Decomposed-coordinated surrogate modeling strategy for compound function approximation in a turbine-blisk reliability evaluation. Aerosp Sci Technol 95:105466. https://doi.org/10.1016/j.ast.2019.105466

    Article  Google Scholar 

  35. Zhu S-P, Keshtegar B, Tian K, Trung N-T (2021) Optimization of load-carrying hierarchical stiffened shells: comparative survey and applications of six hybrid heuristic models. Arch Comput Methods Eng. https://doi.org/10.1007/s11831-021-09528-3

    Article  Google Scholar 

  36. Yaseen ZM, Keshtegar B, Hwang H-J, Nehdi ML (2019) Predicting reinforcing bar development length using polynomial chaos expansions. Eng Struct 195:524–535. https://doi.org/10.1016/j.engstruct.2019.06.012

    Article  Google Scholar 

  37. Ramadan Suleiman A, Nehdi ML (2017) Modeling self-healing of concrete using hybrid genetic algorithm–artificial neural network. Materials 10(2):135

    Article  Google Scholar 

  38. Omar T, Nehdi M, Zayed T (2017) Integrated condition rating model for reinforced concrete bridge decks. J Perform Constr Facil 31(5):04017090

    Article  Google Scholar 

  39. Hasanipanah M, Keshtegar B, Thai D-K, Troung N-T (2020) An ANN-adaptive dynamical harmony search algorithm to approximate the flyrock resulting from blasting. Eng Comput. https://doi.org/10.1007/s00366-020-01105-9

    Article  Google Scholar 

  40. Jaddi NS, Abdullah S (2017) A cooperative-competitive master-slave global-best harmony search for ANN optimization and water-quality prediction. Appl Soft Comput 51:209–224. https://doi.org/10.1016/j.asoc.2016.12.011

    Article  Google Scholar 

  41. Naik B, Nayak J, Behera HS, Abraham A (2016) A self adaptive harmony search based functional link higher order ANN for non-linear data classification. Neurocomputing 179:69–87. https://doi.org/10.1016/j.neucom.2015.11.051

    Article  Google Scholar 

  42. Song C, Wang Y, Puranam A, Pujol S, 445B AS, Usta M (2015) ACI 445B Shear Wall Database.

  43. Hornik K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2(5):359–366

    Article  MATH  Google Scholar 

  44. Geem ZW, Kim JH, Loganathan G (2002) Harmony search optimization: application to pipe network design. Int J Model Simul 22(2):125–133

    Article  Google Scholar 

  45. Omran MG, Mahdavi M (2008) Global-best harmony search. Appl Math Comput 198(2):643–656

    MathSciNet  MATH  Google Scholar 

  46. 318 AC (2014) Building code requirements for structural concrete (ACI 318-14) and commentary on building code requirements for structural concrete (ACI 318R-14)

  47. Keshtegar B, MeAB S (2018) Modified response surface method basis harmony search to predict the burst pressure of corroded pipelines. Eng Fail Anal 89:177–199

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, China

    Behrooz Keshtegar

  2. Department of Civil and Environmental Engineering, Western University, London, ON, Canada

    Moncef L. Nehdi

  3. Institute of Research and Development, Duy Tan University, Da Nang, 550000, Vietnam

    Reza. Kolahchi

  4. Division of Computational Mathematics and Engineering, Faculty of Civil Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Nguyen-Thoi Trung

  5. Faculty of Civil Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Nguyen-Thoi Trung

  6. Department of Civil Engineering, Birjand University of Technology, P.B. 9719866981, Birjand, Iran

    Mansour Bagheri

Authors
  1. Behrooz Keshtegar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Moncef L. Nehdi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Reza. Kolahchi
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Nguyen-Thoi Trung
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Mansour Bagheri
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Moncef L. Nehdi or Reza. Kolahchi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Keshtegar, B., Nehdi, M.L., Kolahchi, R. et al. Novel hybrid machine leaning model for predicting shear strength of reinforced concrete shear walls. Engineering with Computers 38 (Suppl 5), 3915–3926 (2022). https://doi.org/10.1007/s00366-021-01302-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01302-0

Keywords