Skip to main content
Springer Nature Link
Log in

Robust multiscale design of incompressible multi-materials under loading uncertainties

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

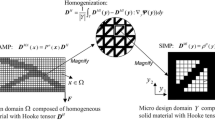
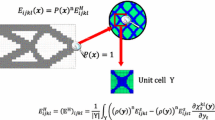
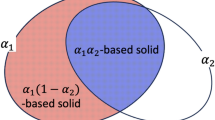
Abstract

Most of the multiscale topology optimization (TO) approaches, which have been proposed for multi-material designs, are based on the assumption of deterministic loads and the exclusion of uncertain quantities like positions, directions, and magnitudes of loads. This contribution deals with: (1) multiscale design; (2) multi-materials; (3) loading uncertainties; and (4) incompressible materials such as rubbers and biological soft tissues. The proposed approach, in this paper is to exploit polytopal composite finite elements (PCEs) to overcome the inherent volumetric locking phenomenon in incompressible materials and employ adaptive geometric components (AGCs) to model porous multi-materials on an analysis grid of PCEs, which allows simultaneously optimizing incompressible multi-materials at both macro- and micro-scales. Besides the mixed displacement–pressure formulation and traditional concurrent TO, the proposed approach is purely developed from the displacement formulation and the AGCs-based direct-multiscale TO whose only constraint is global volume. The effectiveness of the current technique was demonstrated by solving several examples of incompressible porous multi-material designs under single and multiple random loads.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Sussman T, Bathe KJ (1987) A finite element formulation for nonlinear incompressible elastic and inelastic analysis. Comput Struct 26:357–409. https://doi.org/10.1016/0045-7949(87)90265-3

    Article  MATH  Google Scholar 

  2. Sigmund O, Clausen PM (2007) Topology optimization using a mixed formulation: sn alternative way to solve pressure load problems. Comput Methods Appl Mech Eng 196:1874–1889. https://doi.org/10.1016/j.cma.2006.09.021

    Article  MATH  Google Scholar 

  3. Bruggi M, Venini P (2007) Topology optimization of incompressible media using mixed finite elements. Comput Methods Appl Mech Eng 196:3151–3164. https://doi.org/10.1016/j.cma.2007.02.013

    Article  MathSciNet  MATH  Google Scholar 

  4. Srivasista N, Tong L (2012) Design and testing of pressurized cellular planar morphing structures. AIAA J 50:1328–1338. https://doi.org/10.2514/1.J051427

    Article  Google Scholar 

  5. Bruggi M, Venini P (2008) Eigenvalue-based optimization of incompressible media using mixed finite elements with application to isolation devices. Comput Methods Appl Mech Eng 197:1262–1279. https://doi.org/10.1016/j.cma.2007.11.013

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhang G, Alberdi R, Khandelwal K (2018) Topology optimization with incompressible materials under small and finite deformations using mixed u/p elements. Int J Numer Methods Eng 115:1015–1052. https://doi.org/10.1002/nme.5834

    Article  MathSciNet  Google Scholar 

  7. Pereira A, Talischi C, Paulino GH, Ivan IF, Carvalho MS (2016) Fluid flow topology optimization in PolyTop: stability and computational implementation. Struct Multidiscip Optim 54:1345–1364. https://doi.org/10.1007/s00158-014-1182-z

    Article  MathSciNet  Google Scholar 

  8. Bendsoe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224. https://doi.org/10.1016/0045-7825(88)90086-2

    Article  MathSciNet  MATH  Google Scholar 

  9. Groen JP, Sigmund O (2018) Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int J Numer Methods Eng 113:1148–1163. https://doi.org/10.1002/nme.5575

    Article  MathSciNet  Google Scholar 

  10. Sivapuram R, Dunning PD, Kim HA (2016) Simultaneous material and structural optimization by multiscale topology optimization. Struct Multidiscip Optim 54:1267–1281. https://doi.org/10.1007/s00158-016-1519-x

    Article  MathSciNet  Google Scholar 

  11. Li H, Luo Z, Gao L, Qin Q (2018) Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Comput Methods Appl Mech Eng 331:536–561. https://doi.org/10.1016/j.cma.2017.11.033

    Article  MathSciNet  MATH  Google Scholar 

  12. Deng J, Yan J, Cheng G (2013) Multi-objective concurrent topology optimization of thermoelastic structures composed of homogeneous porous material. Struct Multidiscip Optim 47:583–597. https://doi.org/10.1007/s00158-012-0849-6

    Article  MathSciNet  MATH  Google Scholar 

  13. Yan J, Guo X, Cheng G (2016) Multi-scale concurrent material and structural design under mechanical and thermal loads. Comput Mech 57:437–446. https://doi.org/10.1007/s00466-015-1255-x

    Article  MathSciNet  MATH  Google Scholar 

  14. Xia L, Breitkopf P (2017) Recent advances on topology optimization of multiscale nonlinear structures. Arch Comput Methods Eng 24:227–249. https://doi.org/10.1007/s11831-016-9170-7

    Article  MathSciNet  MATH  Google Scholar 

  15. Vicente WM, Zuo ZH, Pavanello R, Calixto TKL, Picelli R, Xie YM (2016) Concurrent topology optimization for minimizing frequency responses of two-level hierarchical structures. Comput Methods Appl Mech Eng 301:116–136. https://doi.org/10.1016/j.cma.2015.12.012

    Article  MathSciNet  MATH  Google Scholar 

  16. Deng J, Pedersen CBW, Chen W (2019) Connected morphable components-based multiscale topology optimization. Front Mech Eng 14:129–140. https://doi.org/10.1002/nme.1620240207

    Article  Google Scholar 

  17. Fu J, Li H, Gao L, Xiao M (2019) Design of shell-infill structures by a multiscale level set topology optimization method. Comput Struct 212:162–172. https://doi.org/10.1016/j.compstruc.2018.10.006

    Article  Google Scholar 

  18. Wadbro E, Niu B (2019) Multiscale design for additive manufactured structures with solid coating and periodic infill pattern. Comput Methods Appl Mech Eng 357:112605. https://doi.org/10.1016/j.cma.2019.112605

    Article  MathSciNet  MATH  Google Scholar 

  19. Groen JP, Wu J, Sigmund O (2019) Homogenization-based stiffness optimization and projection of 2D coated structures with orthotropic infill. Comput Methods Appl Mech Eng 349:722–742. https://doi.org/10.1016/j.cma.2019.02.031

    Article  MathSciNet  MATH  Google Scholar 

  20. Hoang VN, Nguyen NL, Tran P, Qian M, Nguyen-Xuan H (2020) Adaptive concurrent topology optimization of cellular composites for additive manufacturing. JOM 72:2378–2390. https://doi.org/10.1007/s11837-020-04158-9

    Article  Google Scholar 

  21. Hoang VN, Tran P, Vu V-T, Nguyen-Xuan H (2020) Design of lattice structures with direct multiscale topology optimization. Compos Struct 252:112718. https://doi.org/10.1016/j.compstruct.2020.112718

    Article  Google Scholar 

  22. Hoang VN, Tran P, Nguyen N-L, Hackl K, Nguyen-Xuan H (2020) Adaptive concurrent topology optimization of coated structures with nonperiodic infill for additive manufacturing. Comput Des 129:102918. https://doi.org/10.1016/j.cad.2020.102918

    Article  MathSciNet  Google Scholar 

  23. Sigmund O, Torquato S (1997) Design of materials with extreme thermal expansion using a three-phase topology optimization method. J Mech Phys Solids 45:1037–1067. https://doi.org/10.1016/S0022-5096(96)00114-7

    Article  MathSciNet  Google Scholar 

  24. Gibiansky LV, Sigmund O (2000) Multiphase composites with extremal bulk modulus. J Mech Phys Solids 48:461–498. https://doi.org/10.1016/S0022-5096(99)00043-5

    Article  MathSciNet  MATH  Google Scholar 

  25. Luo Z, Tong L, Luo J, Wei P, Wang MY (2009) Design of piezoelectric actuators using a multiphase level set method of piecewise constants. J Comput Phys 228:2643–2659. https://doi.org/10.1016/j.jcp.2008.12.019

    Article  MathSciNet  MATH  Google Scholar 

  26. Huang X, Xie YM (2009) Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials. Comput Mech 43:393–401. https://doi.org/10.1007/s00466-008-0312-0

    Article  MathSciNet  MATH  Google Scholar 

  27. Zhang W, Song J, Zhou J, Du Z, Zhu Y, Sun Z, Guo X (2018) Topology optimization with multiple materials via moving morphable component (MMC) method. Int J Numer Methods Eng 113:1653–1675. https://doi.org/10.1002/nme.5714

    Article  MathSciNet  Google Scholar 

  28. Kazemi H, Vaziri A, Norato JA (2018) Topology optimization of structures made of discrete geometric components with different materials. J Mech Des 140:111401. https://doi.org/10.1115/1.4040624

    Article  Google Scholar 

  29. Wang X, Long K, Hoang VN, Hu P (2018) An explicit optimization model for integrated layout design of planar multi-component systems using moving morphable bars. Comput Methods Appl Mech Eng 342:46–70. https://doi.org/10.1016/j.cma.2018.07.032

    Article  MathSciNet  MATH  Google Scholar 

  30. Hoang VN, Nguyen NL, Nguyen-Xuan H (2020) Topology optimization of coated structure using moving morphable sandwich bars. Struct Multidiscip Optim 61:491–506. https://doi.org/10.1007/s00158-019-02370-z

    Article  Google Scholar 

  31. Carrasco M, Ivorra B, Ramos AM (2012) A variance-expected compliance model for structural optimization. J Optim Theory Appl 152:136–151. https://doi.org/10.1007/s10957-011-9874-7

    Article  MathSciNet  MATH  Google Scholar 

  32. Chen S, Chen W, Lee S (2010) Level set based robust shape and topology optimization under random field uncertainties. Struct Multidiscip Optim 41:507–524. https://doi.org/10.1007/s00158-009-0449-2

    Article  MathSciNet  MATH  Google Scholar 

  33. Lazarov BS, Schevenels M, Sigmund O (2012) Topology optimization considering material and geometric uncertainties using stochastic collocation methods. Struct Multidiscip Optim 46:597–612. https://doi.org/10.1007/s00158-012-0791-7

    Article  MathSciNet  MATH  Google Scholar 

  34. Zhao J, Wang C (2014) Robust topology optimization under loading uncertainty based on linear elastic theory and orthogonal diagonalization of symmetric matrices. Comput Methods Appl Mech Eng 273:204–218. https://doi.org/10.1016/j.cma.2014.01.018

    Article  MathSciNet  MATH  Google Scholar 

  35. Richardson JN, Coelho RF, Adriaenssens S (2016) A unified stochastic framework for robust topology optimization of continuum and truss-like structures. Eng Optim 48:334–350. https://doi.org/10.1080/0305215X.2015.1011152

    Article  MathSciNet  Google Scholar 

  36. Guo X, Zhao X, Zhang W, Yan J, Sun G (2015) Multi-scale robust design and optimization considering load uncertainties. Comput Methods Appl Mech Eng 283:994–1009. https://doi.org/10.1016/j.cma.2014.10.014

    Article  MathSciNet  MATH  Google Scholar 

  37. Cai J, Wang C, Fu Z (2020) Robust concurrent topology optimization of multiscale structure under single or multiple uncertain load cases. Int J Numer Methods Eng 121:1456–1483. https://doi.org/10.1002/nme.6275

    Article  MathSciNet  Google Scholar 

  38. Zheng J, Luo Z, Li H, Jiang C (2018) Robust topology optimization for cellular composites with hybrid uncertainties. Int J Numer Methods Eng 115:695–713. https://doi.org/10.1002/nme.5821

    Article  MathSciNet  Google Scholar 

  39. Zheng J, Luo Z, Jiang C, Gao J (2019) Robust topology optimization for concurrent design of dynamic structures under hybrid uncertainties. Mech Syst Signal Process 120:540–559. https://doi.org/10.1016/j.ymssp.2018.10.026

    Article  Google Scholar 

  40. Deng J, Chen W (2017) Concurrent topology optimization of multiscale structures with multiple porous materials under random field loading uncertainty. Struct Multidiscip Optim 56:1–19. https://doi.org/10.1007/s00158-017-1689-1

    Article  MathSciNet  Google Scholar 

  41. Wu Y, Li E, He ZC, Lin XY, Jiang HX (2020) Robust concurrent topology optimization of structure and its composite material considering uncertainty with imprecise probability. Comput Methods Appl Mech Eng 364:1–43. https://doi.org/10.1016/j.cma.2020.112927

    Article  MathSciNet  MATH  Google Scholar 

  42. Jalalpour M, Tootkaboni M (2016) An efficient approach to reliability-based topology optimization for continua under material uncertainty. Struct Multidiscip Optim 53:759–772. https://doi.org/10.1007/s00158-015-1360-7

    Article  MathSciNet  Google Scholar 

  43. Richardson JN, Filomeno Coelho R, Adriaenssens S (2015) Robust topology optimization of truss structures with random loading and material properties: a multiobjective perspective. Comput Struct 154:41–47. https://doi.org/10.1016/j.compstruc.2015.03.011

    Article  Google Scholar 

  44. Lewis LSK, Chen W (2006) Decision making in engineering design. ASME Press, New York

    Book  Google Scholar 

  45. Beck AT, Gomes WJS, Lopez RH, Miguel LFF (2015) A comparison between robust and risk-based optimization under uncertainty. Struct Multidiscip Optim 52:479–492. https://doi.org/10.1007/s00158-015-1253-9

    Article  MathSciNet  Google Scholar 

  46. Asadpoure A, Tootkaboni M, Guest JK (2011) Robust topology optimization of structures with uncertainties in stiffness - application to truss structures. Comput Struct 89:1131–1141. https://doi.org/10.1016/j.compstruc.2010.11.004

    Article  Google Scholar 

  47. Marler RT, Arora JS (2010) The weighted sum method for multi-objective optimization: new insights. Struct Multidiscip Optim 41:853–862. https://doi.org/10.1007/s00158-009-0460-7

    Article  MathSciNet  MATH  Google Scholar 

  48. Nguyen-Xuan H, Chau KN, Chau KN (2019) Polytopal composite finite elements. Comput Methods Appl Mech Eng 355:405–437. https://doi.org/10.1016/j.cma.2019.06.030

    Article  MathSciNet  MATH  Google Scholar 

  49. Hoang VN, Jang GW (2017) Topology optimization using moving morphable bars for versatile thickness control. Comput Methods Appl Mech Eng 317:153–173. https://doi.org/10.1016/j.cma.2016.12.004

    Article  MathSciNet  MATH  Google Scholar 

  50. Hoang VN, Nguyen-xuan H (2020) Extruded-geometric-component-based 3D topology optimization. Comput Methods Appl Mech Eng 371:113293. https://doi.org/10.1016/j.cma.2020.113293

    Article  MathSciNet  MATH  Google Scholar 

  51. Hoang VN, Nguyen HB, Nguyen-Xuan H (2020) Explicit topology optimization of nearly incompressible materials using polytopal composite elements. Adv Eng Softw 149:102903. https://doi.org/10.1016/j.advengsoft.2020.102903

    Article  Google Scholar 

  52. Saxena A (2011) Topology design with negative masks using gradient search. Struct Multidiscip Optim 44:629–649. https://doi.org/10.1007/s00158-011-0649-4

    Article  Google Scholar 

  53. Nguyen H, Hoang VN, Jang G (2020) Moving morphable patches for three-dimensional topology optimization with thickness control. Comput Methods Appl Mech Eng 368:113186. https://doi.org/10.1016/j.cma.2020.113186

    Article  MathSciNet  MATH  Google Scholar 

  54. Svanberg K (1987) The method of moving asymptotes - a new method for structural optimization. Int J Numer Methods Eng 24:359–373. https://doi.org/10.1002/nme.1620240207

    Article  MathSciNet  MATH  Google Scholar 

  55. Fan HL, Jin FN, Fang DN (2008) Mechanical properties of hierarchical cellular materials. Part I: analysis. Compos Sci Technol 68:3380–3387. https://doi.org/10.1016/j.compscitech.2008.09.022

    Article  Google Scholar 

  56. Ajdari A, Nayeb-Hashemi H, Vaziri A (2011) Dynamic crushing and energy absorption of regular, irregular and functionally graded cellular structures. Int J Solids Struct 48:506–516. https://doi.org/10.1016/j.ijsolstr.2010.10.018

    Article  MATH  Google Scholar 

  57. Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195. https://doi.org/10.1016/j.cma.2004.10.008

    Article  MathSciNet  MATH  Google Scholar 

  58. Khatir S, Abdel Wahab M (2019) A computational approach for crack identification in plate structures using XFEM, XIGA, PSO and Jaya algorithm. Theor Appl Fract Mech 103:102240. https://doi.org/10.1016/j.tafmec.2019.102240

    Article  Google Scholar 

  59. Khatir S, Tiachacht S, Le Thanh C, Bui TQ, Abdel Wahab M (2019) Damage assessment in composite laminates using ANN-PSO-IGA and Cornwell indicator. Compos Struct 230:111509. https://doi.org/10.1016/j.compstruct.2019.111509

    Article  Google Scholar 

  60. Khatir S, Abdel Wahab M (2019) Fast simulations for solving fracture mechanics inverse problems using POD-RBF XIGA and Jaya algorithm. Eng Fract Mech 205:285–300. https://doi.org/10.1016/j.engfracmech.2018.09.032

    Article  Google Scholar 

  61. Nguyen-Xuan H, Liu GR, Bordas S, Natarajan S, Rabczuk T (2013) An adaptive singular ES-FEM for mechanics problems with singular field of arbitrary order. Comput Methods Appl Mech Eng 253:252–273

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This research is funded by Vietnam Maritime University under Grant number: DT2021.04.

Author information

Authors and Affiliations

  1. Mechanical Engineering Institute, Vietnam Maritime University, Haiphong, Vietnam

    Van-Nam Hoang

  2. Department of Aerospace Engineering, University of Michigan, Ann Arbor, USA

    Trung Pham

  3. CIRTECH Institute, Ho Chi Minh City University of Technology (HUTECH), Ho Chi Minh City, Vietnam

    Duc Ho & H. Nguyen-Xuan

  4. Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan

    H. Nguyen-Xuan

Authors
  1. Van-Nam Hoang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Trung Pham
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Duc Ho
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. H. Nguyen-Xuan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to H. Nguyen-Xuan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hoang, VN., Pham, T., Ho, D. et al. Robust multiscale design of incompressible multi-materials under loading uncertainties. Engineering with Computers 38, 875–890 (2022). https://doi.org/10.1007/s00366-021-01372-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01372-0

Keywords